Propiedades de los sólidos platónicos
Anuncio
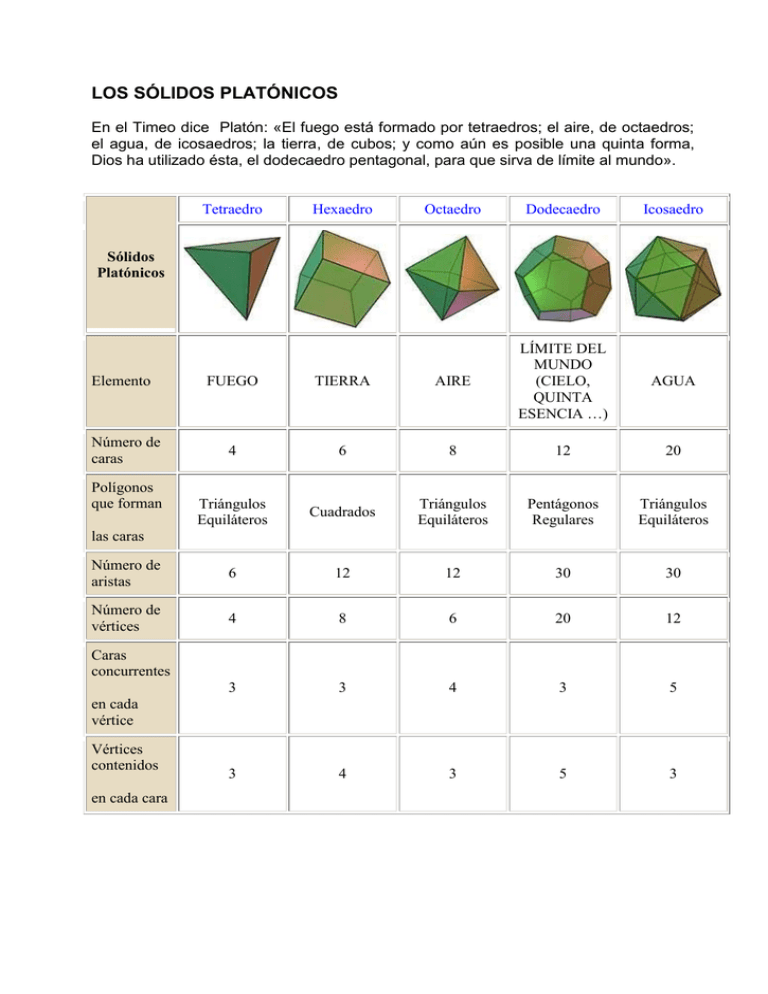
LOS SÓLIDOS PLATÓNICOS En el Timeo dice Platón: «El fuego está formado por tetraedros; el aire, de octaedros; el agua, de icosaedros; la tierra, de cubos; y como aún es posible una quinta forma, Dios ha utilizado ésta, el dodecaedro pentagonal, para que sirva de límite al mundo». Tetraedro Hexaedro Octaedro Dodecaedro Icosaedro AGUA Sólidos Platónicos FUEGO TIERRA AIRE LÍMITE DEL MUNDO (CIELO, QUINTA ESENCIA …) 4 6 8 12 20 Triángulos Equiláteros Cuadrados Triángulos Equiláteros Pentágonos Regulares Triángulos Equiláteros Número de aristas 6 12 12 30 30 Número de vértices 4 8 6 20 12 3 3 4 3 5 3 4 3 5 3 Elemento Número de caras Polígonos que forman las caras Caras concurrentes en cada vértice Vértices contenidos en cada cara tierra fuego Universo agua aire Figuras tomadas del tratado Mysterium Cosmographicum de Kepler Siguiendo a Rüdiger Appel, las razones para estas asociaciones con los elementos podrían deberse a las siguientes razones: El hexaedro o cubo —el poliedro regular más difícil de volcar— fue asociado a la tierra —el ‘elemento’ más estable—.” El tetraedro es el que tiene la relación volumen/superficie menor. Se lo asoció con el fuego, el ‘elemento’ seco.” Platón asoció al dodecaedro con el Universo. Puede haber habido tres razones para ello: a. Se creía que la sustancia de los cuerpos celestes era distinta de la de los cuerpos que rodean al hombre. Por lo tanto, si había 4 elementos y 5 poliedros, el quinto correspondería a la sustancia de la cual estaban hechos los cuerpos celestes. b. Dado que tiene doce caras, pensando en los doce signos del zodíaco, estaba relacionado con el Universo. c. Por sus caras pentagonales, el dodecaedro es el elemento más complejo y distinto de los restantes. “En resumen, no es claro si Platón relacionó al dodecaedro con el Universo (la Naturaleza como Todo), con el cielo (lo exterior a la Tierra) o con el Cosmos (el orden)” “El icosaedro es el que tiene la relación volumen/superficie mayor. Se lo asoció con el agua, el ‘elemento’ húmedo.” El octaedro, si bien puede girar como un trompo, es la figura más fácil de volcar. Se lo asoció con el aire.” Muchos creen que fueron los pitagóricos quienes los concibieron por primera vez. Sin embargo, los arqueólogos han hallado imágenes en piedra de los poliedros regulares considerablemente más antiguas. Imágenes recogidas en un yacimiento neolítico de Escocia Se cree que fue Empédocles el primero que asoció el cubo, el tetraedro, el icosaedro y el octaedro con la tierra, el fuego, el agua y el aire, respectivamente. Estas sustancias eran los cuatro "elementos" de los griegos antiguos. Luego Platón asoció el dodecaedro con el Universo pensando que, dado que era tan distinto de los restantes (por sus caras pentagonales) debía tener relación con la sustancia de la cual estaban hechos los planetas y las estrellas, ya que por entonces se creía que los cuerpos celestes debían estar hechos de un elemento distinto del que estaban hechas las cosas que rodean al hombre en la Tierra. De aquí que a los poliedros regulares se los conozca también como sólidos platónicos. Propiedades de los sólidos platónicos Regularidad Todas las caras de un sólido platónico son polígonos regulares iguales. En todos los vértices de un sólido platónico concurren el mismo número de caras y de aristas. Todas las aristas de un sólido platónico tienen la misma longitud. Todos los ángulos diedros que forman las caras de un sólido platónico entre sí son iguales. Todos sus vértices son convexos a los del icosaedro. Simetría Los sólidos platónicos son fuertemente simétricos: Todos ellos gozan de simetría central respecto a un punto del espacio (centro de simetría) que equidista de sus caras, de sus vértices y de sus aristas. Todos ellos tienen además simetría axial respecto a una serie de ejes de simetría que pasan por el centro de simetría anterior. Todos ellos tienen también simetría especular respecto a una serie de planos de simetría (o planos principales), que los dividen en dos partes iguales. Como consecuencia geométrica de lo anterior, se pueden trazar en todo sólido platónico tres esferas particulares, todas ellas centradas en el centro de simetría del poliedro: Una esfera inscrita, tangente a todas sus caras en su centro. Una segunda esfera tangente a todas las aristas en su centro. Una esfera circunscrita, que pase por todos los vértices del poliedro. Proyectando los centros de las aristas de un poliedro platónico sobre su esfera circunscrita desde el centro de simetría del poliedro se obtiene una red esférica regular, compuesta por arcos iguales de círculo máximo, que constituyen polígonos esféricos regulares. Conjugación: Poliedro dual Si se traza un poliedro empleando como vértices los centros de las caras de un sólido platónico se obtiene otro sólido platónico, llamado conjugado del primero, con tantos vértices como caras tenía el sólido inicial, y el mismo número de aristas. El poliedro conjugado de un dodecaedro es un icosaedro, y viceversa; el de un cubo es un octaedro; y poliedro conjugado de un tetraedro es otro tetraedro. Otros sólidos no regulares Se dice, con razón, que son los únicos poliedros regulares, aunque hay que matizar a continuación “de carácter convexo”. A su vez, Kepler-Poinsot idearon cuatro poliedros cóncavos. Otros sólidos, no regulares, ideados por científicos son (hay más): los sólidos de Arquímedes (son poliedros convexos de caras regulares y vértices uniformes, pero no de caras uniformes); los sólidos de Catalán (se encuentran el triaquistetraedro, el rombododecaedro, el triaquisoctaedro, el tetraquishexaedro, el icositetraedro deltoidal, el hexaquisoctaedro, el icositetraedro pentagonal, el triacontaedro rómbico, el triaquisicosaedro, el pentaquisdodecaedro, el hexecontaedro deltoidal, el hexaquisicosaedro y el hexecontaedro pentagonal: trece en total), etc, etc. Los Poliedros en el Renacimiento. Della Francesca, Luca Pacioli y Durero Los llamados artistas matemáticos del Renacimiento manifestaron gran interés por los poliedros, propiciado, por una parte, por los estudios platónicos sugeridos por la reaparición de ciertos manuscritos con las obras de Platón, y por otra, debido a que estos sólidos servían como excelentes modelos en los estudios sobre Perspectiva. El estudio más completo fue realizado hacia 1480 por Piero della Francesca en su obra Libellus De Quinque Corporibus Regularibus. Aparte de los tópicos euclídeos sobre poliedros, en esta obra se redescubren gradualmente los llamados sólidos arquimedianos o poliedros semirregulares. Son trece cuerpos igualmente inscriptibles en una esfera con caras, polígonos regulares de dos o tres tipos, siendo iguales los polígonos que resultan de unir puntos medios de aristas que concurren en un vértice. Pappus de Alejandría, que atribuye su invención a Arquímedes, da una descripción de estos sólidos en su obra La Colección Matemática e indica, además, para cada sólido, el número de caras, aristas y vértices. Piero della Francesca fue un experto en relacionar los diversos poliedros; obtuvo unos a partir de otros y los inscribió sucesivamente. De esta forma, además del posible número de polígonos regulares en el plano (infinitos) y de poliedros regulares en el espacio (sólo cinco) aparece otra distinción significativa entre ambos tipos de entes: mientras que en el plano, el triángulo, el cuadrado y el pentágono, por ejemplo, son geométrica y algebraicamente independientes unos de otros, los cinco poliedros regulares guardan entre sí íntimas relaciones estructurales. De ellas la más elemental es la llamada dualidad o reciprocidad poliédrica según la cual «el sólido cuyos vértices son los centros de las caras de uno platónico también es platónico» y también «el sólido determinado por los planos tangentes en los vértices a la esfera circunscrita a un sólido platónico también es platónico». Un poliedro y su dual tienen el mismo número de lados y el número de caras de uno es igual al número de vértices del otro. Los cinco poliedros regulares se clasifican por dualidad en tres grupos: tetraedro que es dual de sí mismo, cubo-octaedro (el dual del cubo es el octaedro y viceversa) e icosaedro-dodecaedro (el dual del icosaedro es el dodecaedro y viceversa) según muestran las siguientes figuras: Piero della Francesca va mucho más allá al realizar un estudio muy completo de formas de pasar directa o indirectamente de unos sólidos platónicos a otros, vinculando de múltiples maneras los diversos poliedros. Se puede encontrar un estudio bastante exhaustivo de la interrelación de sólidos platónicos, a base de buscar de forma sistemática las posibles inscripciones entre poliedros regulares dispuestos de tal forma que las simetrías comunes coincidan (por ejemplo, como el cubo y el octaedro tiene las mismas simetrías, se podrán inscribir en los mismos poliedros, y también podrán inscribirse en ellos los mismos poliedros). En particular, al considerar los pares de poliedros (de un tamaño adecuado) que tienen exactamente las mismas simetrías, resultan parejas de sólidos en los que los vértices del poliedro inscrito yacen en los centros de las caras del otro poliedro, que son los pares de poliedros que hemos llamado duales. Grabado de La Divina Proporción de Luca Pacioli La imagen representa una original inscripción de un icosaedro en un cubo, de forma que los vértices del icosaedro están situados sobre las caras del cubo. Luca Pacioli inspirándose en las fuentes platónicas y euclídeas (y en primera instancia pitagóricas), en la obra de Vitrubio, en las conversaciones con Leonardo da Vinci y en los trabajos de Piero della Francesca, realiza la construcción y hace un estudio exhaustivo de los poliedros regulares y semirregulares en su obra La Divina Proporción donde abundan las referencias esotéricas. Diseños de Leonardo da Vinci del icosaedro y del dodecaedro que aparecen en la obra de Luca Pacioli La Divina Proporción (Venecia, 1509). El famoso cuadro realizado por J. de Barbari en 1495 (Museo de Capidemonte, Nápoles) que representa a Luca Pacioli rodeado de elementos geométricos alusivos a una página de Euclides, en relación con los poliedros, a cuyo estudio está dedicada gran parte de su famosa obra La Divina Proporción. En la pintura aparece el dodecaedro como símbolo de unión mística entre maestro y discípulo (que representa a Guidobaldo, Duque de Urbino, aunque alguno ha querido ver a un joven Durero), así como uno de los poliedros arquimedianos llamado por Kepler RomboCuboOctaedro, posiblemente redescubierto por Pacioli. Pacioli estudia la proporción mutua de todas las superficies poliédricas regulares y la inclusión progresiva de cada uno de los poliedros en el siguiente, hasta el punto de que el dodecaedro los contiene a todos. La influencia pitagórico-platónica le infunde la veneración hacia el dodecaedro, al que llama nobilísimo cuerpo regular, de forma que interpretando El Timeo platónico, escribe (La Divina Proporción, Cap. LV): «La forma de doce bases pentagonales la atribuyó [Platón] al cielo como aquello que es receptáculo de todas las cosas, del mismo modo que el dodecaedro es receptáculo y albergue de todos los cuerpos regulares, como se puede comprobar por la inscripción de un cuerpo en otro». Los trabajos de Piero della Francesca y Luca Pacioli sobre poliedros tuvieron una gran incidencia en la posterior Literatura matemática vinculada al Arte, sobre todo la desarrollada por Durero en su obra de 1525 con el nombre de De la Medida. Se trata de una especie de enciclopedia geométrica para uso de pintores, redactada por un gran maestro artista-geómetra formado en el cruce de las tradiciones prácticas, artesanas, sabias, artísticas y humanistas, que pretendía dotar a la creación artística de una base científico-geométrica. Buena parte del Libro IV de la obra de Durero está dedicada a los poliedros regulares y semiregulares. Para Durero los poliedros regulares son sólidos «que son iguales en todo, caras, ángulos y lados, a los que Euclides llama “corpora regularia” Él describe cinco, pues no pueden ser otros que los que se inscriben en su totalidad tangentes a una esfera». A continuación, Durero describe, uno por uno, los cinco poliedros regulares, indica el número de caras, aristas y vértices, y representa cada uno de los cuerpos por su desarrollo en un plano y por dos proyecciones ortogonales sobre los planos horizontal y vertical, lo que, en alguna medida, es un antecedente de la Geometría Descriptiva. Ejemplos de Poliedros en el Arte del siglo XX: Gaudí y Dalí Las formas poliédricas en el Arte de Gaudí Gaudí desarrolló una capacidad casi milagrosa de utilizar todas las formas geométricas y no sólo como nueva morfología estética sino como componente estructural desde la perspectiva gravitatoria de las cargas, es decir, la estética al servicio de la estática. Se definía así mismo como geómetra («yo soy geómetra que quiere decir hombre de síntesis») y al considerar la naturaleza como fuente de inspiración de muchas de sus formas geométricas, Gaudí escribía: «en la naturaleza está el principio y el fin de todas las formas». No es extraño, pues, que las formas poliédricas fueran un tópico habitual para Gaudí. Gaudí utilizó luces en forma de dodecaedro tanto en la cripta de la Sagrada Familia como en la catedral de Palma de Mallorca y es curioso saber que colgaban del techo de su obrador algunos poliedros. En los pináculos de los campanarios la Sagrada Familia, tanto en la fachada del Nacimiento como en la de la Pasión, aparecen complejas formas resultantes de la intersección de diversos poliedros (sobre todo cubos y octaedros) con esferas provistas de vaciados cilíndricos funcionales que crean espacios donde situar la original iluminación. En los cuatro pináculos de los campanarios de la fachada de la Gloria están presentes dodecaedros regulares. Según Alsina (2002):«Si en las proporciones de la Sagrada Familia, Gaudí optó por las relaciones 1/4, 1/3, 1/2, 2/3, 3/4, 1, asociadas a los divisores de 12 y hay doce campanarios con pináculos, no es de extrañar que los tres poliedros regulares que intervienen sean el cubo y el octaedro de 12 aristas y el dodecaedro de doce caras». El misticismo poliédrico en la creatividad de Dalí Para Dalí, como para otros muchos artistas, la Geometría proporciona importantes argumentos en las reflexiones teóricas previas a la obra de arte. En particular la Divina Proporción y los poliedros regulares, además de las implicaciones estéticas acreditadas por su presencia en algunos de sus cuadros, asumen una función de orden cosmológico, científico, teológico y simbólico. En la aplicación constante de la Matemática a su pintura, Dalí sintetiza siglos de tradición simbólica pitagórica. Dalí se había interesado en los años 30 del pasado siglo por las investigaciones de M. Ghyka acerca de la sección áurea, la geometría y la numerología pitagóricas, lo que deja una huella en su arte que adquiere una estrecha relación entre Ciencia y Religión (Weyers, 2000). Como reminiscencia platónica la mitología en torno al dodecaedro le ha servido a Dalí para evocar y asumir una fuerte carga simbólica en algunas de sus composiciones. 1. Dalí. El Sacramento de la Eucaristía en la Última Cena. 1955. Colección Chester Dale. Galería Nacional de Arte. Washington. La Última Cena tiene lugar bajo la quintaesencia del Dodecaedro cósmico, el símbolo pitagórico-platónico del universo. 2. Dalí. A la búsqueda de la cuarta dimensión. Óleo sobre tela. Colección particular 1979. La pareja de espaldas recuerda a Platón y Aristóteles en La Escuela de Atenas, de Rafael. 3. Dalí. Corpus hypercubus. 1954. Metropolitan Museum of Art, Nueva York. Representación de la Crucifixión de Cristo en una cruz que geométricamente es una yustaposición de ocho cubos (Baig, 1990), desarrollo tridimensional de un hipercubo tetradimensional (de forma análoga al desarrollo de un cubo de tres dimensiones en una figura plana en forma de cruz). «Al pintar la cruz [de esta forma] Dalí simboliza la creencia cristiana ortodoxa de que la muerte de Cristo fue un acontecimiento metahistórico, que tuvo lugar en una región [el más allá], que trasciende a nuestro tiempo y espacio tridimensional» (Gardner, 1981).

