Esfera Definición: Propiedades Importantes
Anuncio
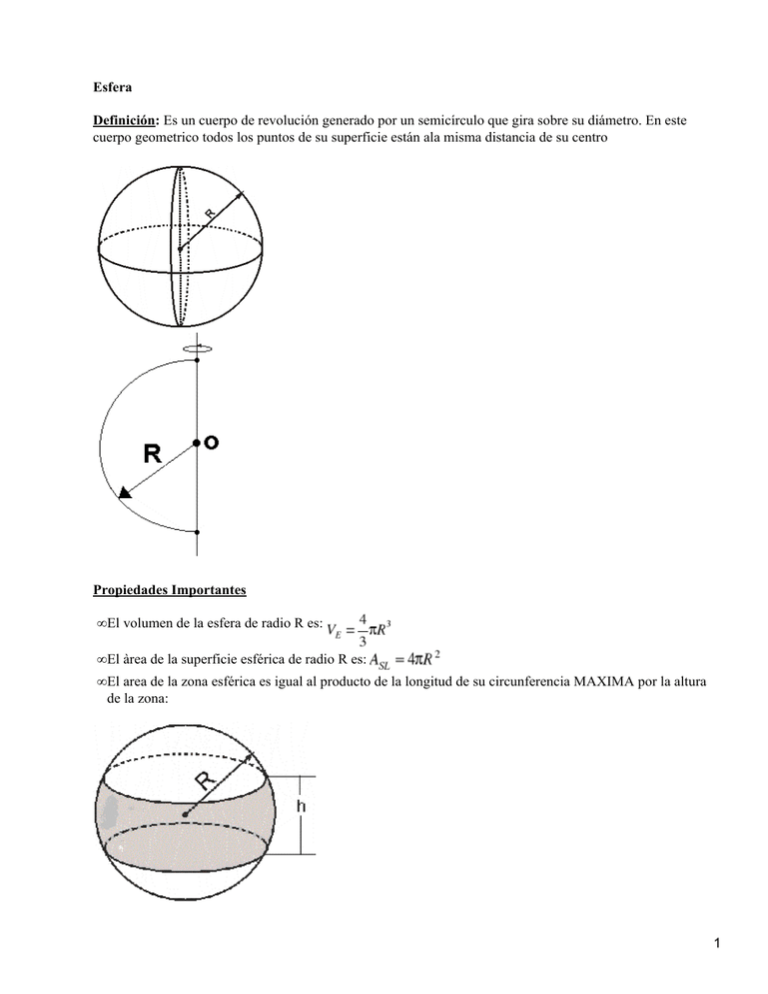
Esfera Definición: Es un cuerpo de revolución generado por un semicírculo que gira sobre su diámetro. En este cuerpo geometrico todos los puntos de su superficie están ala misma distancia de su centro Propiedades Importantes • El volumen de la esfera de radio R es: • El àrea de la superficie esférica de radio R es: • El area de la zona esférica es igual al producto de la longitud de su circunferencia MAXIMA por la altura de la zona: 1 • El área de una superficie esférica es le cuádruple del área de uno de sus círculos máximos. • El área de una superficie esférica es igual al área lateral del cilindro circunscrito EJERCICIOS • Hallar el área del circulo máximo de una superficie esfera cuya área es 16m2 Solución: Sabemos que Por dato ASE=16m2 16m2 = • Siendo el radio y la altura del cono de 6 y 8 hallar el area de la esfera inscrita Solución: Graficando se tiene: 2 • 4 esferas cuyos radios de su superficies esférica miden 15cm y tangentes entre si se le colocan sobre una mesa perfectamente horizontal, formando una especie de pirámide con 3 de ellas como base. Calcular la altura de la pirámide. Solución: Graficando se tienes: Al unir los centros de las superficies esféricas se determina un tetraedro regular cuya arista mide 2r. Por formula: La altura de la pirámide de formada por las esferas será: Altura Altura Reemplazamos datos: Altura Altura • hallar la longitud de la altura de la zona esférica de1884 m2 de área , en una esfera de 30 m de radio. 3 Solución: Graficando se tiene: • un plano secante a una esfera determina en ella un círculo menor de área 18 cm2. si dicho plano dista 12cm del centro de la esfera, hallar el área de la superficie y el volumen de esta ultima. Solución: • Una esfera tiene 3m de radio ¿a que distancia del centro debe trazarse un plano secante para que la sección obtenida sea 1/3 del circulo máximo. Solución: Graficando se tienes: • Dos esferas cuyos radios miden 4 y 6 m son tangentes exteriores y se encuentran apoyados sobre una mesa. Hallar la distancia entre los puntos de apoyo. Solución: Graficando: 4 Según formula: • Tres esferas de radio 4, 9 y 16 se encuentran sobre una mesa tangentes exteriores dos a dos. Hallar el perímetro del triangulo que se forma al unir los puntos de tangencia de las esferas con la mesa. Solución: AB= BC= AC= Perímetro ABC = 12 + 24 + 16 = 52 5 • Hallar la longitud del radio de la esfera sabiendo que su área es numéricamente igual a su volumen. Solución: Asl = VE 4R2=(4/3) R3 R=3 • La suma de las áreas A1, A2, A3, de tres esferas es 196 m2, el radio de la primera, es el doble de la segunda, y el de la tercera es media proporcional de los dos primeros. Hallar el área mayor Solución: • Según dato: A1 tiene R1=2R2 A2 tiene R2 A3 tiene R3 = • A1 + A2+ A3 = 196 (4R12) + (4R22) + (4R32) = 196 4(2R2)2 + (4R22) + 4( )2 =196 16R22 + 4R22 + 8R22 = 196 28 R22=196 R22 = El área mayor es A1 A1 = 4R12 A1 = 4(2R2)2 A1 = 16R22 A1 = 16 A1 = 112m2 • BC2=AB2+AC2 6 BC=10 • El "ABC "ODB Ase = 4r2 Ase = 36m2 1884 =2(30)h 31.4 = h 10 = h • En el circulo menor: r2=81cm2 r = 9cm • En el "OMC por teorema de Pitágoras : R2=122+r2 R=15cm • Area de la superficie esferica: A = 4R2 A = 900cm2 • Volumen de la esfera V = (4/3) R3 V = 4500cm3 • A circulo mínimo= (1/3)A circulo maximo • A circulo maximo = r12 =9m2 Reeplaso en el primer dato: • A circulo mínimo = (1/3)( 9) A circulo mínimo = 3m2 • Como: r22=3 r2 = • Por Pitágoras: r12 = r22 + d2 d2 = 9 − 3 7 d= • 8