4.4. Determine la magnitud, sentido y la dirección del momento de
Anuncio
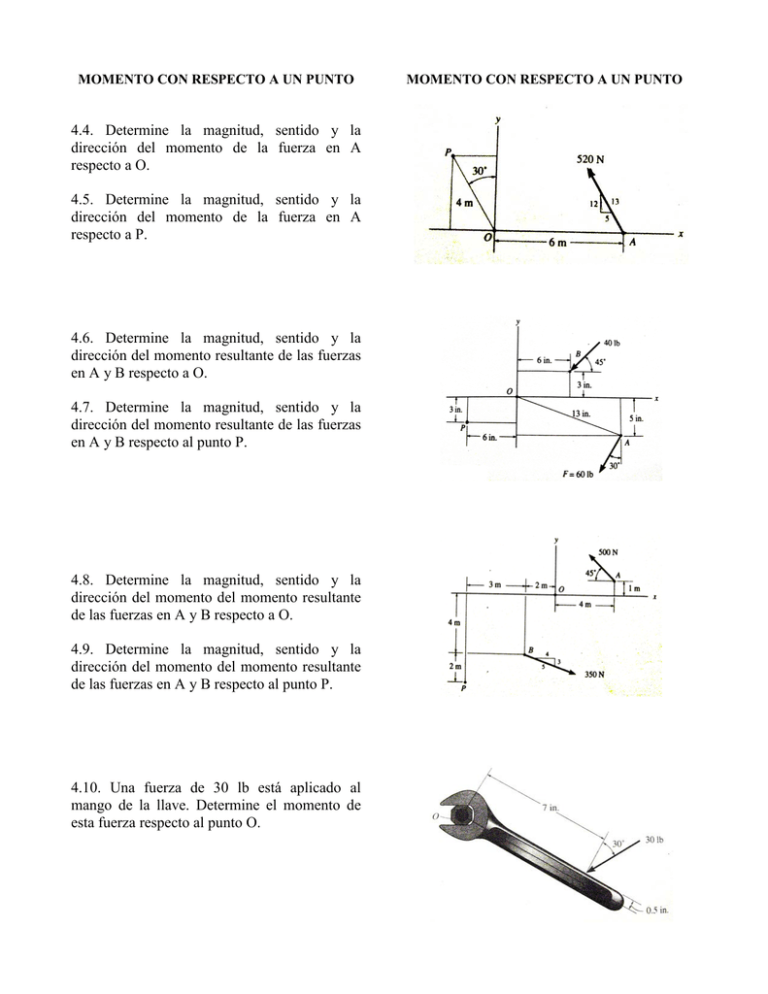
MOMENTO CON RESPECTO A UN PUNTO 4.4. Determine la magnitud, sentido y la dirección del momento de la fuerza en A respecto a O. 4.5. Determine la magnitud, sentido y la dirección del momento de la fuerza en A respecto a P. 4.6. Determine la magnitud, sentido y la dirección del momento resultante de las fuerzas en A y B respecto a O. 4.7. Determine la magnitud, sentido y la dirección del momento resultante de las fuerzas en A y B respecto al punto P. 4.8. Determine la magnitud, sentido y la dirección del momento del momento resultante de las fuerzas en A y B respecto a O. 4.9. Determine la magnitud, sentido y la dirección del momento del momento resultante de las fuerzas en A y B respecto al punto P. 4.10. Una fuerza de 30 lb está aplicado al mango de la llave. Determine el momento de esta fuerza respecto al punto O. MOMENTO CON RESPECTO A UN PUNTO 4.11. Un hombre intenta levantar un marro con una mano; si la cabeza del marro pesa 10 lb, determine el ángulo máximo θ en lo que puede sostener, si el momento máximo que puede desarrollar en la muñeca es 18 lb*ft. Se ignora el peso del mango. 4.13. Determine el momento resultante respecto al punto A de las tres fuerzas que actúan sobre la viga. 4.14. Determine el momento resultante respecto al punto B de las tres fuerzas que actúan sobre la viga. 4.16. Determine la orientación θ (0°≤ θ ≤90°) de la fuerza F de 40 lb, de modo que F produzca; (a) el momento máximo respecto de A, y (b) ningún momento respecto de A. Calcule el momento en cada caso. 4.17. Determine el momento de la fuerza F respecto a A como función de θ. Trace la gráfica de M (ordenada) vs. θ (abscisa) para 0°≤ θ ≤180°. 4.18. Un hombre ejerce las dos fuerzas en el mango de la pala. Determine el momento resultante de estas fuerzas respecto de la hoja de la pala en A. 4.19. Las tenazas se usan para sujetar los extremos del tubo de perforación P. Determine el torque (momento) Mp de la fuerza aplicada F=150 lb ejerce sobre el tubo como función de θ. Grafique este momento Mp vs. θ para 0°≤ θ ≤90°. 4.20. Se usan las tenazas para sujetar los extremos del tubo de perforación P. Si se necesita en torque (momento) de Mp =800 lb*ft en P para girar el tubo, determine la fuerza del cable F que debe aplicarse a las tenazas. Considere que θ=30°. 4.21. Determine el momento de la fuerza F en A respecto al punto O. Exprese el resultado como vector cartesiano. 4.22. Determine el momento de la fuerza F en A respecto al punto P. Exprese el resultado como vector cartesiano. 4.23. Determine el momento resultante de las fuerzas respecto a O. Exprese el resultado como vector cartesiano. 4.24. Determine el momento resultante de las fuerzas respecto a P. Exprese el resultado como vector cartesiano. 4.25 Un cable ejerce una fuerza de 140N en el poste de teléfonos como se ilustra. Determine el momento de esta fuerza en la base A del poste. Resuelva el problema de dos maneras, esto es, usando un vector de posición de A a C, y luego. De A a B. 4.26. Utilizando vectores cartesianos, calcule el momento de cada una de las dos fuerzas que actúan en el ensamble tubular respecto al punto O. Sume estos momentos y calcule la magnitud y ángulos directores coordenados del momento resultante. Nota: F2 = 60 i – 10 j – 35 k N. 4.27. Usando vectores cartesianos, determine el momento de cada una de las dos fuerzas que actúan sobre el ensamble tubular respecto al punto A. Sume estos momentos y calcule la magnitud y ángulos directores coordenados del momento resultante. Nota: F2 = 60 i – 10 j – 35 k N. 4.28 El tubo curvo tiene un radio de 5 ft. Si una fuerza de 80 lb actúa en su extremo como se ilustra, determine el momento de esta fuerza respecto al punto C. Resuelva el problema usando dos diferentes vectores de posición. 4.29. Una fuerza F de magnitud F = 100 N actúa a lo largo de la diagonal del paralelepípedo. Usando vectores cartesianos, determine el momento de F respecto al punto A, donde MA = rB x F y MA = rC x F. 4.30. Encuentre el momento resultante de las dos fuerzas que actúan en el extremo del ensamble tubular respecto a cada unión A, B y C. 4.31. Si F = 50i + 60j + 30k lb, determine la magnitud y ángulos directores coordenados del momento de F respecto al punto A. 4.32. Determine los ángulos directores coordenados de la fuerza F aplicada al extremo del tubo, de modo que el momento creado por F respecto al punto A sea cero. 4.33. La varilla curva tiene un radio de 4 ft y se encuentra sostenida por el cable AB, que ejerce una fuerza de 80 lb sobre la varilla. Determine el momento de esta fuerza respecto a C. Resuelva el problema usando dos diferentes vectores de posición. 4.34. El equipo de rayos x se utiliza para diagnósticos médicos. Si la cámara y la caja en C tienen una masa de 150kg y centro de masa en G, determine el momento de su peso respecto al punto O, cuando se encuentre en la posición mostrada. 4.35. El ensamble tubular ésta sujeto a la fuerza de 80 N. Determine el momento de esta fuerza respecto al punto A. 4.36. El ensamble tubular ésta sujeto a la fuerza de 80 N. Determine el momento de esta fuerza respecto al punto B. 4.37. El momento en el punto P creado por la fuerza aplicada F que actúa en la caja, es Mp = - i - 3j - 9k [lb*in]. Determine las dimensiones b y c de la caja. 4.38. Una fuerza F= -5i + 3j - 4k kN produce un momento de Mo = -17i - 7j + 16k kN m respecto al punto O. Si la fuerza actúa en un punto P de coordenada y = 2m, determine sus coordenadas x y z. 4.39. La fuerza F=-5i + 3j - 4k kN crea un momento respecto al punto O de Mo = -17i - 3j + 19k kN m . Si la fuerza pasa por un punto P que tiene z = 3m, determine las otras dos coordenadas de este punto. También teniendo en cuenta que Mo = Fd, determine la distancia perpendicular d, desde el punto O hasta la línea de acción de F. 4.40. Una fuerza de F = 6i + 2j + k kN produce un momento de Mo = 4i + 5j - 14k kN m respecto al origen, O. Si la fuerza actúa en un punto que tiene su primera coordenada x = 1m, determine las otras dos coordenadas. 4.41. La fuerza F = 6i + 8j + 10k N crea un momento respecto a O de Mo = -14i + 8j + 2k N m. Si la fuerza pasa por un punto que tiene x = 1m, determine sus otras dos coordenadas. También, observando que Mo = Fd, determine la distancia perpendicular del punto O a la línea de acción de F. MOMENTO CON RESPECTO A UN EJE MOMENTO CON RESPECTO A UN EJE 4.42. Determine el momento de la fuerza F alrededor del eje Oa. Exprese el resultado como un vector cartesiano. ’ 4.43. Determine el momento resultante de dos fuerzas alrededor de eje aa’. Exprese el resultado como un vector cartesiano. 4.44 Determine el momento de la fuerza F alrededor del eje aa’. Determine el resultado como un vector cartesiano. 4.45. Determine el momento resultante de las dos fuerzas alrededor del eje Oa. Exprese el resultado como un vector cartesiano. 4.46. Determine los momentos de la fuerza F respecto a los ejes x, y z. Resuelva el problema (a) con enfoque vectorial cartesiano y (b) con el enfoque escalar ’ 4.47. Determine el momento de la fuerza F respecto a un eje que une los puntos O y A. Exprese el resultado como vector cartesiano 4.48. Determine la magnitud del momento resultante de las tres fuerzas respecto al eje AB. Resuelva el problema (a) con enfoque vectorial cartesiano y (b) con el enfoque escalar. 4.49. Una fuerza F = 8i – j + k lb se aplica al mango de la llave. Determine la componente del momento de esta fuerza respecto al eje z que tiene efecto en apretar el perno. 4.50. La cadena AB ejerce una fuerza de 20 lb sobre la puerta en B. Determine la magnitud del momento de esta fuerza respecto al eje de las bisagras de esta puerta, el eje x. 4.51. Se usan las dos llaves en combinación para quitar la tuerca de la maza de la rueda. Si la fuerza aplicada al final de la llave de caja es F= 4i - 12j + 2k N, determine la magnitud del momento de esta fuerza respecto al eje x que es eficiente para sacar la tuerca. 4.52. La fuerza de 50 lb actúa sobre el engrane en la dirección mostrada. Determine el momento de esta fuerza respecto al eje y. 4.53. Determine el momento que la fuerza F ejerce respecto al eje y que es el eje de la flecha. Resuelva el problema mediante los métodos vectorial, cartesiano y escalar. Exprese el resultado como vector cartesiano. 4.54. En la ménsula actúa una fuerza de 600 N aplicada en el punto A. Determine el momento de esta fuerza respecto al eje y. 4.55. Una fuerza de 50 N se aplica a la manija de la puerta. Determine el momento de esta fuerza respecto al eje z de las bisagras. Ignore el tamaño de la manija. Sugerencia: use análisis escalar. 4.56. La fuerza de F=80 lb actúa a lo largo de la arista DB del tetraedro. Determine la magnitud del momento de esta fuerza respecto a la arista AC. 4.57. Si el momento de la fuerza F respecto a la arista AC del tetraedro tiene una magnitud de M=200 lb*ft y se dirige de C a A, determine la magnitud de F.