Objetivo 2.2.2 Proyecciones axonometricas Angulos y coeficientes

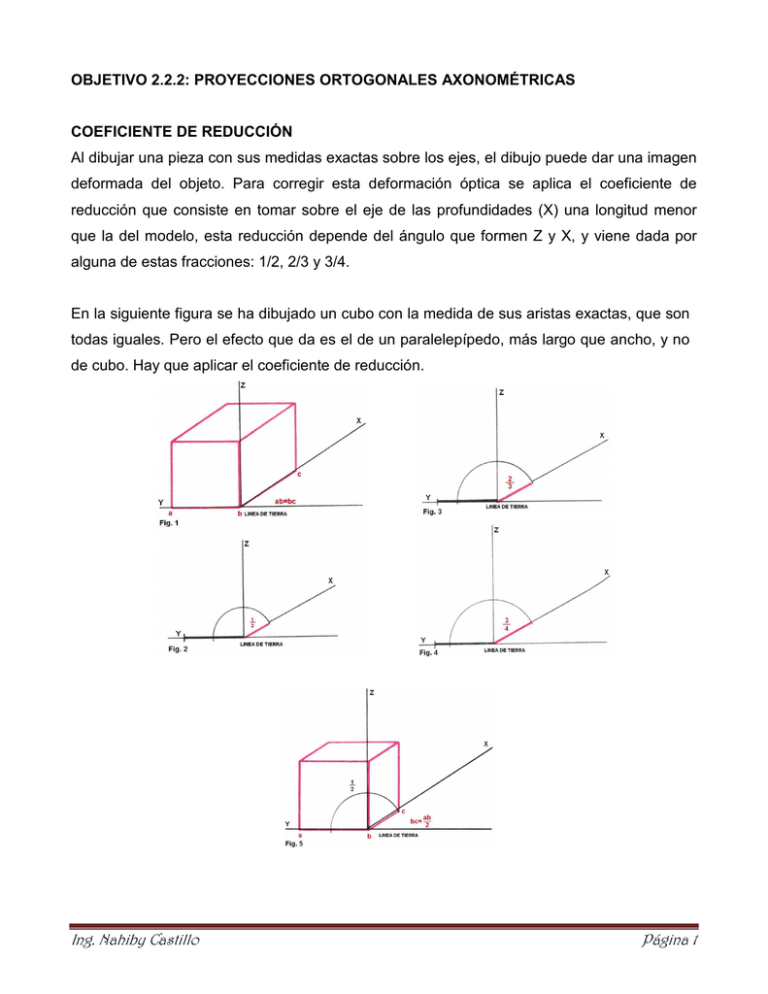
OBJETIVO 2.2.2: PROYECCIONES ORTOGONALES AXONOMÉTRICAS
COEFICIENTE DE REDUCCIÓN
Al dibujar una pieza con sus medidas exactas sobre los ejes, el dibujo puede dar una imagen
deformada del objeto. Para corregir esta deformación óptica se aplica el coeficiente de
reducción que consiste en tomar sobre el eje de las profundidades (X) una longitud menor
que la del modelo, esta reducción depende del ángulo que formen Z y X, y viene dada por
alguna de estas fracciones: 1/2, 2/3 y 3/4.
En la siguiente figura se ha dibujado un cubo con la medida de sus aristas exactas, que son
todas iguales. Pero el efecto que da es el de un paralelepípedo, más largo que ancho, y no
de cubo. Hay que aplicar el coeficiente de reducción.
Ing. Nahiby Castillo
Página 1
PERSPECTIVA AXONOMÉTRICA: Un dibujo es realizado en perspectiva o proyección
axonométrica cuando se representa en un sistema de ejes. En ellos se determinan: el
ancho, la profundidad y la altura de un objeto.
LÍNEAS ISOMÉTRICAS: Son todas las líneas que sean paralelas a cualquiera de los tres
ejes isométricos.
En el dibujo isométrico de un sólido regular (cubo, paralelepípedo) todas las líneas son
isométricas.
CONSTRUCCIÓN DE UN SISTEMA DE EJES ISOMÉTRICOS
Procedimiento:
1.- Trazamos la línea de tierra y levantamos una perpendicular a ella.
2.- Con escuadras de 30° trazamos los ángulos, guiá ndonos por la línea de tierra.
Ing. Nahiby Castillo
Página 2
Ejemplo: Realizar el dibujo isométrico del siguiente paralelepípedo:
Procedimiento:
1.- Tomemos como vértice del sistema de ejes el vértice A del
paralelepípedo. Trazamos la línea de tierra y levantamos el eje
perpendicular.
A
2.- Con escuadras de 30° trazamos los otros dos eje s.
A
3.- A partir del origen A, y sobre el respectivo eje, llevamos distancias iguales a la altura,
ancho y profundidad del paralelepípedo dado:
4.- Desde los puntos B, C, y G trazamos paralelas
a
los
ejes
isométricos
y
obtenemos
el
paralelepípedo. No deben trazarse las líneas
ocultas de la figura.
Ing. Nahiby Castillo
Página 3
LÍNEAS NO ISOMÉTRICAS: Son todas aquellas líneas NO paralelas a ningún eje
isométrico
Las líneas no isométricas no se toman en su
verdadera magnitud, es decir, no se pueden
medir directamente del objeto (como sucede en
las líneas isométricas). En consecuencia deben
construirse determinando sus puntos extremos,
mediante las líneas isométricas (es decir, líneas
paralelas a los ejes).
Igualmente los ángulos no se proyectan al dibujo en su verdadera magnitud sino partiendo
de sus proyecciones ortogonales (perpendiculares).
Ing. Nahiby Castillo
Página 4
Ejercicio:
Realizar el dibujo isométrico del siguiente sólido:
Procedimiento:
1.- Trazamos un sistema de ejes isométricos. Tomemos
como origen del sistema el vértice B de la figura (se
puede tomar otro vértice).
2.- A partir del origen G, y sobre el respectivo eje,
llevamos las distancias:
[B, G] = Altura
[B, A] = Ancho
[B, C] = Profundidad
3.- Trazamos las líneas isométricas, es decir, las líneas
paralelas a los ejes isométricos (las medidas deben ser
igual a las del objeto, exactas).
i)
[A, F] y [C, D] paralelas a [B, G]
ii)
[F, E] y [D, H] paralelas a [B, C]
iii) [E, D], [H, I], [F, J], [G, K] paralelas a [A, B]
iv) [J, I] paralelas a [B, C]
v) [J, K] paralelas a [B, G]
4- Determinamos las líneas no isométricas uniendo K
con I y G con H. Verifica que las distancias [K, I] y [G, H]
del dibujo son distintas a las del modelo.
Ing. Nahiby Castillo
Página 5