modulo geodesia

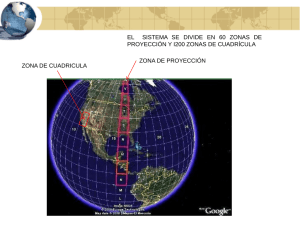
MODULO
MODULO GEODESIA
GEODESIA
Alfredo Solorza M. - Ing. Geomensor
MODELO DE LA TIERRA
N
b
φ
ecuador
a
S
TIPOS DE SUPERFICIES
H = ALTURA ORTOMETRICA
h = ALTURA ELIPSOIDAL
N = ONDULACION GEODAL
Tipos de coordenadas
- Geocéntricas
X,Y,Z
- Geodésicas
Latitud, Longitud, h y H
- Universal Transversal Mercator
N,E
Ejemplo:
X= 1697623.540 m.
Y= -5052184.376 m.
Z= -3491742.572 m.
Latitud=
-33° 24’ 25”.25899
Longitud= -71° 25’ 36”.25874
Altura= 23.258 m
Norte= 6300957.404 m.
Este= 274324.009 m.
Apoyo visual
Diferencia de distancia
entre tipos de superficies
Como obtengo la distancia
horizontal de terreno?
Sup. terrestre
DH
h
KH
Elipsoide
h
DH= DG * KH
KH= (R+ HP)/R
DG
Reducción con origen UTM
R
R
-Calculo de nuevas distancias
-Calculo de azimut
Hablemos de la proyección
UTM
PROYECCIÓN UTM
Los cubrimientos cartográficos regular y básico del país han sido desarrollados
esencialmente en la proyección Universal Transversal de Mercartor (UTM).
La proyección nativa utilizada corresponde a la Transversal de Mercator (TM).
Utiliza 60 proyecciones del mismo tipo con un meridiano central propio, para cubrir
la totalidad del globo en el sentido longitudinal, cada una con un ancho
correspondiente a un huso de 6° sexagesimales, llamadas ZONAS o HUSOS UTM.
La extensión meridional de cada zona es entre los 84° de latitud norte, y los 80°
latitud sur y estos Husos numerados del 1 al 60, progresando desde el Este, a
partir de los 180° de longitud Oeste.
El Meridiano central con factor reductor
de 0,9996 y valor de cuadrícula 500.000
m, crecientes hacia el Este y decrecientes
hacia el Oeste y el Ecuador con valor de
cuadrícula 0 m para el hemisferio norte y
en aumento hacia el polo norte, y de
10.000.000 m para el caso del hemisferio
sur, disminuyendo hacia el polo sur.
Hemisferio SUR
Norte Falso: 10.000.000
Este Falso: 500.000
MC: ??
Ko: 0.9996
PROYECCIÓN UTM
De este modo las coordenadas planas resultantes serán las UTM
correspondiendo a Chile los siguientes Husos UTM independientemente de
la existencia de cartografía regular en alguno de ellos:
Chile Continental Husos 18 y 19
Chile Insular Huso 12 (Isla de Pascua)
Huso 13 (Isla San Félix, Isla San Ambrosio)
Huso 17 (Archipiélago De Juan Fernández)
Territorio Antártico Husos 16,17,18,19,20,21 y 22
PROYECCIÓN UTM
Entonces:
Para una coordenada:
75° w
78° w
69° w
72° w
66° w
Ecuador
Huso 18
Huso 19
Entonces para grandes
extensiones de superficie, que
hacemos?
Sup. terrestre
DH
h
KH
Elipsoide
h
DH= DG * KH
KH= (R+ HP)/R
DG
R = 6378000
R
R
Reducción en distancia y
azimut
PROYECCIÓN DE COORDENADAS
Coordenadas geodésicas
Latitud, Longitud
Parámetros para proyectar en UTM
Generación de un LTM -PTL
FN= 10.000.000
FN= 7.000.000
FE= 500.000
FE= 200.000
MC = ?
MCL = ?
Ko = 0.9996
Ko = KH
OBTENCIÓN DE PARÁMETROS PARA UN LTM-PTL
70° 30’ W
71° W
70° W
900
600
300
T= 1/20.000
DV= T * R
FN = 7.000.000
FE = 200.000
MCL = 70.5 W
Ko= KH=
OBTENCIÓN DE PARÁMETROS
70° 30’ W
71° W
69° 30’ W
69° W
70° W
1500
1200
900
600
300
T= 1/20.000
DV= T * R
SISTEMAS DE REFERENCIA
(DATUM)
1.- SISTEMAS DE REFERENCIA TOPOCENTRICOS
2.- SISTEMAS DE REFERENCIA GEOCENTRICOS
3.- SISTEMAS DE REFERENCIA INERCIALES
1.- TOPOCENTRICOS: 2D, Latitud, Longitud, la altura es independiente y
se utiliza la altura al NMM (H).
Ejemplos de Datums topocéntricos o regionales en el país.
- Sudamericano de 1969, ubicado en Chua, Brasil.
- Provisorio Sudamericano de 1956, ubicado en La Canoa, Venezuela.
- Hito XVIII, Ubica en la zona austral de Chile.
b
φ
a
2.- GEOCENTRICOS: 3D, Latitud, Longitud, la altura referida al elipse (h).
Ejemplos de Datums geocéntricos o globales.
- Sistema Geodésico Mundial (WGS-84).
2.- INERCIALES: 4D, Latitud, Longitud, la altura referida al elipse (h),
velocidad.
Ejemplos de Datums inerciales ITRF.
- SIRGAS (DATUM ACTUAL DE CHILE).
ELIPSOIDES DE REFERENCIA
UTILIZADOS EN CHILE
Internacional o
Hayford 1924
Sudamericano
de 1969 o
Australiano
Geodetic
Reference
System 1984
Geodetic
Reference
System 1980
IMPORTANCIA DE LOS
SISTEMAS DE REFERENCIA
(DATUM)
RED GEODÉSICA NACIONAL
PSAD-56
SAD-69
WGS-84
Precisión de las redes trigonométricas PSAD-56, SAD-69
Primer Orden Geodésico 1:100000 = 10 ppm
Precisión de las redes SIRGAS (WGS-84)
Primer Orden Geodésico superior a 1:100000 = 10 ppm
Precisión de una base cartográfica
Concepto de MUC a ¼ de mm.
Transformación de
DATUM
Métodos de transfromación
de Datum
-Siete parámetros ( Bursa Wolfe )
-Molodensky
-Cartesiana o trigonométrica
Siete parámetros
3 Traslaciones ∆X, ∆Y, ∆Z
3 Rotaciones r1, r2 ,r3
1 Factor de escala
z
y
x
Molodensky – Trigonométrica o cartesiana
3 Traslaciones ∆X, ∆Y, ∆Z
z
y
x
Ecuaciones simplificadas de
molodensky
Trigonométrica o cartesiana
Ecuación de transformación
X2= X1+ ∆X
Y2= Y2 + ∆Y
Z2= Z1 + ∆Z
Parámetros de transfromación de datum, definidos por la Agencia
Nacional Estadounidense de imágenes y mapas – NIMA
Precisión 30 m. APP
Parámetros para Transformación de
DATUM
Precisión 5 m.
Como obtener parámetros específicos para
un área:
Puntos de control en el área de estudio
Donde:
WGS-84
N =
PSAD-56
a
N =
1 − e 2 ( sen ϕ ) 2
a
1 − e 2 ( sen ϕ ) 2
X = ( N + H ) cos ϕ cos λ
X = ( N + H ) cos ϕ cos λ
Y = ( N + H ) cos ϕ sen λ
Y = ( N + H ) cos ϕ sen λ
Z = ( N (1 − e 2 ) + H ) sen ϕ
Z = ( N (1 − e 2 ) + H ) sen ϕ
∆X = XB − X
A
∆Z = ZB −ZA
∆ Y = YB − Y A
Consideración H=0
MODULO
MODULO GEODESIA
GEODESIA
FIN
FIN
Alfredo Solorza M. - Ing. Geomensor