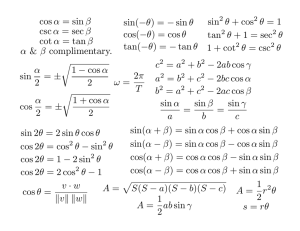Trigonometry Identities Reciprocal Identities sin θ

Trigonometry Identities
Double-Angle Identities
Reciprocal Identities
1
sin θ
1
sec θ =
cos θ
1
cot θ =
tan θ
1
csc θ
1
cos θ =
sec θ
1
tan θ =
cot θ
csc θ =
sin θ =
Quotient Identities
tan θ =
sin θ
cos θ
cot θ =
cos θ
sin θ
Pythagorean Identities
sin2 θ + cos2 θ = 1
2
2
1 + tan θ = sec θ
1 + cot2 θ = csc2 θ
Even-Odd Identities
sin (−θ) = − sin θ
csc (−θ) = − csc θ
cos (−θ) = cos θ
sec (−θ) = sec θ
tan (−θ) = − tan θ
cot (−θ) = − cot θ
Sum and Difference Identities
sin (α + β) = sin α cos β + cos α sin β
sin (α − β) = sin α cos β − cos α sin β
cos (α + β) = cos α cos β − sin α sin β
cos (α − β) = cos α cos β + sin α sin β
tan α + tan β
tan (α + β) =
1 − tan α tan β
tan α − tan β
tan (α − β) =
1 + tan α tan β
sin 2θ = 2 sin θ cos θ
cos 2θ = cos2 θ − sin2 θ = 2 cos2 θ − 1
2 tan θ
tan 2θ =
1 − tan2 θ
Half-Angle Identities
1 − cos θ
θ
=±
sin
2
2
θ
1 + cos θ
cos
=±
2
2
θ
1 − cos θ
sin θ
1 − cos θ
tan
=±
=
=
2
1 + cos θ
sin θ
1 + cos θ
Power-Reducing Identities
1 − cos 2θ
sin2 θ =
2
1 + cos 2θ
cos2 θ =
2
1
−
cos
2θ
tan2 θ =
1 + cos 2θ
Law of Sines
b
c
a
=
=
sin A
sin B
sin C
Law of Cosines
a2 = b2 + c2 − 2bc cos A
b2 = a2 + c2 − 2ac cos B
c2 = a2 + b2 − 2ab cos C
Product to Sum
1
sin A cos B = [sin (A − B) + sin (A + B)]
2
1
sin A sin B = [cos (A − B) − cos (A + B)]
2
1
cos A cos B = [cos (A − B) + cos (A + B)]
1
2
The Unit Circle
y
2
√
2 2
2 2,
√
4
2
60 ◦
120
13
45 ◦
◦
π
1
2
◦
5
6
◦
150 ◦
π
√ 3 ,
π
90
◦
4
5π
6
(−1, 0)
,
3
π
2π
3
3π
− √
3
2 , 1
2
2
1
π
2
√
3
√ 3
−1 , 2
2
√ 2
√ 2 , 2
2
−
(0, 1)
30
0◦
180◦
(1, 0)
0
x
◦
330 ◦
210
240 ◦
22
◦
5
5π
4
4π
3
− √
2 2
√ 3
2
−1
2 , − √
3
2
,
√ 2
− 2
√ 2 2 ,
2
1 ,−
− √
2 2
4
2
3π
2
(0, −1)
√
3
2 , −1 5π
3
270
◦
7π
◦
31
−1
√
− 3 , 2
2
11
π
6
300
5◦
7π
6
The above image is provided courtesy of Wikipedia and is licensed for use under the GNU
Free Documentation License, Version 1.2 or any later version published by the Free Software
Foundation. More information about the original creator can be found at the website:
http://en.wikipedia.org/wiki/Image:Unit_circle_angles.svg
2