Área del círculo

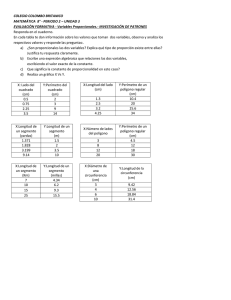
Profr. Efraín Soto Apolinar.
Material de Distribución Gratuita
¿Cómo podemos calcular el área de un círculo?
Si nosotros dibujamos un círculo, podemos dibujar un polígono regular de n lados inscrito en él, como se muestra
enseguida:
A5
A6
A7
n =5
n =6
n =7
A8
A9
A 10
n =8
n =9
n = 10
Si hacemos que el número de lados del polígono regular se haga muy grande, el área del polígono se parecerá cada
vez más al área del círculo.
Ahora vamos a calcular el área del polígono de n lados. Para eso, vamos a dividirlo en triángulos con base en los
lados del polígono como se muestra en la siguiente figura.
···
b3
b2
···
Ahora vamos a calcular el área de un triángulo.
Dado que todos los triángulos que hemos dibujado tienen la misma área,
cuando multipliquemos el área de un triángulo por n obtendremos el área
del polígono regular inscrito al círculo.
Observa que el perímetro del polígono regular es muy parecido al de la
circunferencia. Cuando n es muy grande, la diferencia es muy pequeña
que podemos considerarlas iguales.
Pero el perímetro del polígono es igual a la suma de las bases de los triángulos que dibujamos a partir del polígono.
b1
bn
La altura de un triángulo es prácticamente igual al radio del círculo. Entonces el área de cada triángulo es: A t =
b i × r /2. Y la suma de las áreas de todos los triángulos es igual al área del polígono, y aproximadamente igual al
área del círculo:
Ac ≈ Ap
=
=
b1 · r b2 · r
bn · r
+
+ ··· +
2
2
2
r
· (b 1 + b 2 + · · · + b n )
2
La suma de todas las bases de los triángulos es igual al perímetro del polígono inscrito al círculo. Pero ya dijimos
que este perímetro es prácticamente igual al perímetro de la circunferencia, que es igual a 2πr . Sustituyendo esto
en la fórmula para calcular el área obtenemos:
Ac ≈ Ap =
r
r
· (b 1 + b 2 + · · · + b n ) = · (2πr ) = πr 2
2
2
Cuando el número n de lados del polígono es muy grande, el perímetro del polígono es igual a la longitud de la
circunferencia y la fórmula para calcular el área del círculo es:
A c = πr 2
efra.soto.a@gmail.com