Sí - Ejercicios de física y matemática
Anuncio

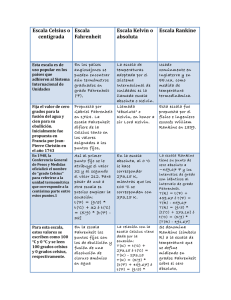
ESCALAS TERMOMETRICAS 1.- En Gran Bretaña aún se usa la escala Rankine, en donde la relación con la escala Kelvin es t°R = 95 tK. Determine los puntos de fusión y ebullición del agua en la escala. Datos: TF = 0ºC TE = 100ºC TK = TC + 273 TFK = 0 + 273 = 273 K TR = 9 x 273 / 5 = 491.4 ºR TK = TC + 273 TEK = 100 + 273 = 373 K TR = 9 x 373 / 5 = 671.4 ºR 2.- La temperatura de ebullición del oxígeno es de 90,19 K. Determine dicha temperatura en las escalas Celsius, Fahrenheit y Rankine. Datos: TE = 90,19 K Celsius) T = TK – 273 = 90,19 – 273 = -182,81 ºC Fahrenheit) T = 9TC / 5 + 32 = 9 x (-182,81) / 5 + 32 = -297,058 ºF Rankine) T = 9TK/5 = 9 x 90,19 / 5 = 162,342 ºR Expresar la temperatura normal del cuerpo, 37°C, en las escalas: Fahrenheit, Kelvin. © 3.- o .c l Datos: TC = 37 ºC u g Fahrenheit) T = 9TC / 5 + 32 = 9 x 37 / 5 + 32 = 98,6 ºF Kelvin) T = TC + 273 = 37 + 273 = 310 K Si es que las hay. ¿A qué temperaturas son iguales (los valores numéricos) las escalas: a) Celsius y Fahrenheit; b) Kelvin y Fahrenheit; c) Kelvin y Celsius? a) TC = TF = x v e rd 4.- .h TF = 9TC / 5 + 32 w w x = 9x/5 + 32 x – 32 = 9x/5 5(x-32) = 9x 5x – 160 = 9x 4x = -160 x = -40º TF = 9TC / 5 + 32 (1) w b) TK = TF = x TK = TC + 273 (2) Si se despeja TC de (1), se tiene: TC = 5(TF − 32) 9 y se sustituye en (2), se tiene: TK = 5(TF − 32) 5( x − 32) + 273 , y al reemplazar por x, se tiene: x = + 273 9 9 Y, finalmente, despejando, se tiene: x = 574,25 c) TK = TC = x Hernán Verdugo Fabiani Profesor de Matemática y Física www.hverdugo.cl 1 TK = TC + 273 x = x + 273 273 = 0 Se concluye, entonces, que no existe un valor en donde coincidan las escalas Kelvin y Celsius. Además, debe tomarse en cuenta que ambas escalas son similares, solo que están desplazadas 273º, por lo tanto también de esto se deduce que no pueden coincidir. 5.- El punto de ebullición normal del helio es 2,2 K; una temperatura ambiente confortable es 295 K; la superficie del Sol está a una temperatura en torno a los 6.000 K; el interior de una estrella está a una temperatura de alrededor de diez millones de K. Expresar estas temperaturas en: a) escala Celsius; b) escala Fahrenheit a) 2,2 K = TC + 273 TC = -270,8 ºC 295 K = TC + 273 TC = 20 ºC 6.000 K = TC + 273 5.727 ºC b) 2,2 K = -270,8 ºC TF = 9 ● (-270,8)/5 + 32 = -455,44 ºF 295 K = 20 ºC TF = 9 ● 20 / 5 + 32 = 68 ºF 6.000 K = 5.727 ºC TF = 9 ● 5.727 / 5 + 32 = 10.340,6 ºF 6.- ¿En qué valor numérico, una medida de temperatura en la escala Celsius es el doble que en la escala Fahrenheit? © Datos: TF = x TC = 2x l TF = 9TC/5 + 32 x = 9 ● 2x / 5 + 32 5 (x – 32) = 18x 5x – 160 = 18x 13x = - 160 Termito acaba de inventar, para su uso personal, una escala termométrica, en donde se pudo saber que: la fusión del agua se produce a los 100 °ter y cada grado ter equivale a 2°C. Determine: a) la temperatura de ebullición del agua en °ter, b) el 0°ter en °C, c) el cero absoluto en °ter. e rd u g o 7.- .c x = -12,3 º .h v Datos: 0°C = 100°ter 1° ter = 2°C w w w a) A nivel del mar la ebullición del agua ocurre a 100°C, pero esa cantidad equivale a 50° ter según los datos. Por lo tanto, la temperatura en °ter sería 100°ter + 50° ter = 150 ° ter. b) 0°ter es 100°ter menos que la temperatura de fusión del agua, por lo tanto equivale a 200°C menos que la fusión del agua, entonces 0°ter = - 200°C c) 0 K = - 273°C, y como por cada 2°C hay 1°ter, entonces 273°C = 136,5°ter, por lo tanto, en °ter, el cero absoluto sería 136,5°ter menos que el valor en que ocurre la fusión del agua, es decir, sería -36,5°ter. 8.- ¿En qué valor numérico la temperatura medida en la escala Fahrenheit es el doble que en la escala Celsius? Datos: TC = x TF = 2x TF = 9TC/5 + 32 2x = 9 ● x / 5 + 32 5 (2x – 32) = 9x 10x – 160 = 9x x = 160 9.- Un día de verano se registra una temperatura mínima de 10º C y una máxima de 32ºC. Determine el intervalo de temperatura (variación térmica) de ese día en: a) grados Celsius, b) Kelvin, c) grados Fahrenheit. Datos: Hernán Verdugo Fabiani Profesor de Matemática y Física www.hverdugo.cl 2 Tmin = 10 ºC Tmax = 32 ºC a) ∆T = Tmax - Tmin = 32 ºC – 10 ºC = 22 ºC b) TminK = 10 + 273 = 283 K TmaxK = 32 + 273 = 305 K ∆T = Tmax - Tmin = 305 K – 283 K = 22 K c) TminF = 9 ●10 / 5 + 32 = 50 ºF TmaxF = 9 ●32 /5 + 32 = = 89,6 ºF ∆T = Tmax - Tmin = 89,6 ºF – 50 ºF = 39,6 ºF 10.- Determine la variación térmica de un día de invierno en que se registra una temperatura mínima de 0ºC y una máxima de 12ºC, en: a) grados Celsius, b) Kelvin, c) grados Fahrenheit. a) ∆T = Tmax - Tmin = 12 ºC – 0 ºC =12 ºC b) TminK = 0 + 273 = 273 K TmaxK = 12 + 273 = 285 K © Datos: Tmin = 0 ºC Tmax = 12 ºC o TminF = 9 ●0 / 5 + 32 = 32 ºF TmaxF = 9 ●12 /5 + 32 = = 53,6 ºF u g c) .c l ∆T = Tmax - Tmin = 285 K – 273 K = 12 K ∆T = Tmax - Tmin = 53,6 ºF – 32 ºF = 21,6 ºF e rd Un objeto A tiene una temperatura de –20ºC y otro B tiene una temperatura de 40ºC, se ponen en contacto y luego de un tiempo llegan a un equilibrio térmico en 15ºC. Determine cuántos grados subió el objeto A y cuántos grados bajó el objeto B, en: a) grados Celsius, b) Kelvin, c) grados Fahrenheit. w w Datos: TAC = - 20 ºC TBC = 40 ºC TEqC = 15 ºC .h v 11.- ∆TAC = TEqC - TAC = 15 ºC - -20 ºC = 35 ºC ∆TBC = TEqC - TBC = 15 ºC - 40 ºC = - 25 ºC b) TAK = - 20 + 273 = 253 K TBK = 40 + 273 = 313 K TEqK = 15 + 273 = 288 K w a) ∆TAK = TEqK - TAK = 288 K – 253 K = 35 K ∆TBK = TEqK - TBK = 288 K – 313 K = - 25 K c) TAF = 9 ●(- 20)/5 + 32 = - 4 ºF TBF = 9 ● 40 / 5 + 32 = 104 ºF TEqF = 9 ● 15 / 5 + 32 = 59 ºF ∆TAF = TEqF - TAF = 59 ºF - - 4 ºF = 63 ºF ∆TBF = TEqF - TBF = 59 ºF – 104 ºF = - 45 ºF Hernán Verdugo Fabiani Profesor de Matemática y Física www.hverdugo.cl 3 12.Averigüe la temperatura de fusión y de ebullición del cloro (fusión 171 K; ebullición 239 K). Con esos valores idee una escala termométrica donde la temperatura de fusión del cloro sea 0º y la de ebullición sea de 100º. Con esta nueva escala termométrica, expresada en °Cl, encuentre la equivalencia con: a) 100ºC, b) 0ºC, c) 100ºF, d) 0ºF, e) 0ºK. Datos: Tf = 171 K = -102 °C 0 °Cl Te = 230 K = -43 °C 100 °Cl a) 100 °C = x 100 − ( −102) − 43 − ( −102) = x = 342,37 °Cl x−0 100 − 0 b) 0°C = x 0 − ( −102) − 43 − ( −102) = x = 172,88 °Cl x−0 100 − 0 c) 100 °F = x TF = 9TC/5 + 32 TC = 5(TF – 32)/9 TC = 5(100 – 32)/9 = 37,8 °C entonces: 37,8 °C = x entonces: .c l 0 °F = x TF = 9TC/5 + 32 TC = 5(TF – 32)/9 TC = 5(0 – 32)/9 = -17,8 °C -17,8 °C = x e) e rd u g − 17,8 − ( −102) − 43 − ( −102) = x = 142,71 °Cl x−0 100 − 0 o d) © 37,8 − ( −102) − 43 − ( −102) = x = 236,91 °Cl x−0 100 − 0 0 K = x -273 °C = x w Bárbara, la gran amiga de Ernesto, inventó su propia escala termométrica y la definió a partir de los siguientes puntos de referencia: a la temperatura de 10 ºC le asignó el valor 0 ºB, y a los 170 ºC le asignó el valor 100 ºB. Determine, en ºB, la temperatura de 50 ºC. Datos: T1C = 10 ºC T2C = 170 ºC TC = 50 ºC w w 13.- .h v − 273 − ( −102) − 43 − ( −102) = x = -289,8 °Cl x−0 100 − 0 T1B = 0 ºB T2B = 100 ºB TB = x TB − T1B T2B − T1B T −0 100 − 0 = B = TC − T1C T2C − T1C 50 − 10 170 − 10 TB = 40 x 100 / 160 = 25 ºB Hernán Verdugo Fabiani Profesor de Matemática y Física www.hverdugo.cl 4