detallada - IES Francisco Grande Covián
Anuncio

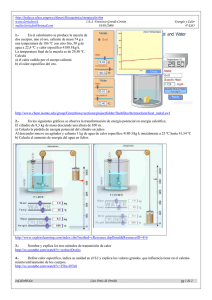
www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 5.Una placa conductora cargada positivamente crea en sus proximidades un campo eléctrico uniforme E = 1000 V/m. tal y como se indica en la figura. Desde un punto de la placa se lanza un electrón con velocidad v = 107 m/s formando un ángulo α = 60º con dicha placa, de forma que el electrón describirá una trayectoria como la indicada en la figura. a) En el punto A, el más alejado de la placa, ¿con qué velocidad se mueve el electrón? Respecto al punto inicial, ¿cuánto ha variado su energía potencial electrostática? Calcula la distancia d entre el punto A y la placa. b) Determina la velocidad (módulo y orientación) del electrón cuando choca con la placa (punto B). Datos: e = 1,6.10–19 C, me = 9,1 10–31 kg. Zaragoza Septiembre 98 r r r r 5,0 ⋅10 6 i + 0 j m / s ; +3,42 10–17 J ; 0,21 m; 10 7 cos 60i + 10 7 sen 60 (− j ) m / s SOLUCIÓN ENERGÉTICA a) En el punto mas alejado de la placa (punto mas alto de la trayectoria) la componente de la velocidad vertical es cero y solo se mantier r ne la componente horizontal 107 cos 60 = 5,0 ⋅10 6 i + 0 j m / s El trabajo en general: WAB = ∆Ec El trabajo en campos conservativos: WAB = − ∆Ep Luego − ∆Ep = ∆Ec , ∆Ep = − ∆Ec = Ec( Final ) − Ec( Inicial ) ( ) ( ) 2 1 1 1 1 ∆Ep = − m(v0 cos α )2 − mv02 = 9,1 ⋅ 10 − 31 107 cos 60 − 9,1 ⋅ 10 − 31 ⋅ 107 2 2 2 2 2 = 3,42 ⋅ 10 −17 J WAB = −∆Ep = −3,42 ⋅ 10−17 J = F ⋅ e ⋅ cos ϕ = qE ⋅ d ⋅ cos180 − 3,42 ⋅ 10 −17 = 1,6 ⋅ 10 −19 ⋅ 1000 ⋅ d ⋅ cos180 ; d = 0,21 m b) Como no hay variación de energía potencial la energía potencial permanece constante, el módulo permanece constante, la componente horizontal de la velocidad es constante y lo único que cambia en sentido es la componente vertical de la velocidad. r r En el punto de lanzamiento la velocidad es 107 cos 60i + 107 sen 60 j m / s r r En el punto B: 10 7 cos 60i + 10 7 sen 60 (− j ) m / s SOLUCIÓN CINEMÁTICA: a) qE La aceleración vertical con que se mueve el electrón vale: q ⋅ E = m ⋅ a ; a = y sentido contrario al del campo. m qE v ⋅ sen α ⋅ m En el punto mas alto la velocidad vertical es cero. v y = v0 sen α − t1 = 0 . t1 = 0 = 4,93 ⋅ 10 −8 s m q⋅E El espacio vertical recorrido d es: d = v0 sen α ⋅ t − 1 q⋅E 2 t = 0,21 m 2 m b) El punto B se caracteriza por tener una ordenada vertical y=0 y = v0 sen α ⋅ t 2 − ´1 q ⋅ E 2 t2 = 0 2 m 2v sen α ⋅ m ´1 q ⋅ E = 9,85 ⋅ 10 −8 s Sacando factor común: t2 v0 sen α − t2 = 0 ; t 2 = 0 q ⋅ E 2 m el tiempo t2 tiene que ser por simetría el doble del t1 La velocidad horizontal v x = v0 cos α = 5 ⋅ 106 m / s la velocidad vertical: v y = v0 sen α − socamele.doc q⋅E t 2 = 8,66 ⋅ 106 m / s m Luis Ortiz de Orruño pg 1 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com socamele.doc I.E.S. Francisco Grande Covián 09/07/2003 Luis Ortiz de Orruño Campo Eléctrico Física 2ªBachiller pg 2 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 12.Se tienen dos cargas eléctricas de 3 µC cada una, una positiva en el origen de coordenadas y la otra negativa, a una distancia de 20 cm. En el sentido positivo del eje de las X. Calcular la intensidad del campo eléctrico y el potencial eléctrico en los siguientes puntos: a) En el punto medio del segmento que las une. b) En un punto equidistante 20 cm de ambas cargas. Datos. Medio en el vacío. Constante de la ley de Coulomb, K= 9 109 N m2 C–2 Madrid. Junio, 1996 a) Dibujamos en A los vectores campo eléctrico creados por la carga positiva(saliente) y la negativa(entrante), los módulos valen: r N 310 −6 E + = 9 ⋅10 9 = 2,7 ⋅10 6 y C (0,1) 2 r N 310 −6 E − = 9 ⋅10 9 = 2,7 ⋅10 6 2 C (0,1) r r N La intensidad de campo vectorial será: ET = 5,4 ⋅10 6 i C El potencial vale: + 3 ⋅10 −6 − 3 ⋅10 −6 V = 9 ⋅10 9 + 9 ⋅10 9 =0 0,1 0,1 0,1 1 = ; ϕ = 60º b) En el triángulo rectángulo ABC cos ϕ = 0,2 2 En B descomponiendo los vectores, las componentes verticales se anulan r r ET = 2 E + cos ϕ i ; tanto en B como en D ; ( ) ( ) r 310 −6 N = 6,75 ⋅10 5 E + = 9 ⋅10 9 2 C (0,2) r r r N ET = 2 ⋅ 6,75 ⋅10 5 ⋅ cos 60 i = 6,75 ⋅10 5 i C V = 9 ⋅10 9 (+ 3 ⋅10 ) + 9 ⋅10 (− 3 ⋅10 ) = 0 socamele.doc −6 0,2 −6 9 0,2 Luis Ortiz de Orruño pg 3 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 15.Dos cargas positivas de 5 µC cada una, situadas en el eje de las X, una en el origen y la otra a 10 cm en el sentido positivo del eje X a) calcular el campo eléctrico en módulo, dirección y sentido, en x= 2 cm b) calcular el potencial eléctrico en x = 15 cm b) ¿En qué punto del eje de las X el campo es cero? Datos: K = 1 4πε 0 = 9 ⋅10 9 N m 2 C − 2 r q La intensidad de campo creado por una carga puntual vale en módulo: E = k 2 , dirección la de la recta que une el r punto y las cargas y sentido saliente si es positiva y entrante si es negativa. r r r 5 ⋅10 −6 En A E1 = 9 ⋅10 9 = 112,5 ⋅10 6 N / C ; E1 = 112,5 ⋅10 6 i N / C 2 (0,02) − r r r N 5 ⋅10 6 E 2 = 9 ⋅10 9 = 7,03 ⋅10 6 N / C ; E 2 = 7,03 ⋅10 6 (−i ) 2 C (0,08) r r r r 6 ET = E1 + E 2 = 105,47 ⋅10 i N / C b) En B V = 9 ⋅10 9 r r c) en C E1 = E 2 9 ⋅10 9 5 ⋅10 −6 x 2 socamele.doc 5 ⋅10 −6 5 ⋅10 −6 + 9 ⋅10 9 = 1,2 ⋅10 6 V 0,15 0,05 = 9 ⋅10 9 5 ⋅10 −6 (0,1 − x ) 2 ; sacando la raiz cuadrada de los dos medios Luis Ortiz de Orruño 1 1 = ; resolviendo x = 0,05 m x 0,1 − x pg 4 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 21.Dos cargas puntuales de 8 µC y –5 µC están situadas, respectivamente, en los puntos (0, 0) y (1, l). Calcula: a) La fuerza que actúa sobre una tercera carga de 1 µC situada en el punto(2,2). b) El trabajo necesario para llevar esta última carga desde el punto que ocupa hasta el punto (0, l). Datos: K = 9,00 109 N. m 2 C–2. Las coordenadas se dan en metros. Galicia 98. : r r r F = 0,0135(cos 45(− i ) + sen 45(− j )) ; 0,033 J S De acuerdo con la ley de Coulomb Entre las cargas de +8 y 1 microculombio la fuerza es de REPULSIÓN y vale: r 8 ⋅ 10 −6 ⋅ 1 ⋅ 10 −6 F1 = 9 ⋅ 109 = 9 ⋅ 10 − 3 N 2 22 + 22 Entre las cargas de +8 y -5 microculombio la fuerza es de ATRACCIÓN y vale: r 5 ⋅ 10 −6 ⋅ 1 ⋅ 10−6 F2 = 9 ⋅ 109 = 22,5 ⋅ 10 − 3 N 2 12 + 12 Restando los módulos de las fuerzas queda: 0,0135 N r r r La fuerza como vector: F = 0,0135 cos 45 − i + sen 45 − j El trabajo realizado por una fuerza conservativa es independiente de la trayectoria e igual a la variación de energía potencial cambiada de signo. + 8 ⋅ 10−6 − 5 ⋅ 10 −6 V(2, 2 ) = 9 ⋅ 109 + 9 ⋅ 109 = − 6364 V 8 2 ( ( ) ( )) + 8 ⋅ 10 −6 − 5 ⋅ 10 −6 + 9 ⋅ 109 = 27000 V 1 1 = −∆E p = −q ⋅ ∆V = −1 ⋅ 10−6 ⋅ (27000 − (− 6364)) = 0,033 J V(0,1) = 9 ⋅ 109 Wcons socamele.doc Luis Ortiz de Orruño pg 5 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 22.Una esferita de 10 gramos de masa cuelga de un hilo sujeto a la placa superior como se indica en la figura. Si la. distancia entre las placas es de 5 cm y la diferencia de potencial es de 103 V. a) Dibuja la dirección y sentido del campo eléctrico y calcula su módulo. b) ¿Cuál es el signo y el valor de la carga eléctrica que debe tener la esfera para que la tensión del hilo sea nula? a) Las líneas de campo salen de la placa positiva y termina en la negativa, estando repartidas uniformemente b) Las fuerzas que actúan sobre la esferita son el peso y la fuerza eléctrica (la tensión se anula r ∆V 10 3 N = = 2 ⋅10 4 Felec = q E ; E = − 2 − ∆r 5 ⋅10 C El peso : mg: 10 10–3 g Igualando: q ⋅ 2 ⋅10 4 = 10 ⋅10 −3 g ; Despejando q = 4,9 10–6 C El signo de la carga tiene que ser negativo para que la fuerza eléctrica compense el peso. socamele.doc Luis Ortiz de Orruño pg 6 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 23.Supón que junto a la superficie de la Tierra existe, además de su campo gravitatorio g = 10 N/kg un campo eléctrico uniforme dirigido en vertical y hacia arriba E = 104 N/C. En esta región soltamos una partícula de masa m = 0,01 kg. con velocidad inicial nula. a) Cuál debe ser su carga para que permanezca en reposo? b) Si la carga de la partícula es el doble de la que acabas de calcular, realizará un movimiento ascendente. ¿Por qué? Calcula su velocidad cuando haya ascendido 2 m respecto al punto inicial. Zaragoza Junio 97 positiva, 1 10–5 C ; 6,3 m/s S socamele.doc Luis Ortiz de Orruño pg 7 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 26.Dos partículas con cargas q1 = 1 µC y q2 = 2 µC están separadas una distancia d = 0,5 m. a) Calcula la fuerza que actúa sobre la segunda y su energía potencial electrostática. b) Si q2 puede moverse, partiendo del reposo, ¿hacia dónde lo hará? Calcula su energía cinética cuando se haya desplazado 0,2 m respecto a su posición inicial. ¿Cuánto trabajo habrá realizado hasta entonces el campo eléctrico? Constante de Coulomb: K =9 109 N.m2.C–2. Zaragoza 98. 0,072 N de repulsión; 0,036 J ; 0,011 J ; 0,011J; hacia pot decre. S La fuerza por ser cargas de igual signo es de repulsión. r Qq 1 ⋅ 10 −6 ⋅ 2 ⋅ 10 −6 = 0,072 N Aplicamos la ley de Coulomb F = K 2 = 9 ⋅ 109 r (0,5)2 b) Hacia la derecha, porque va dirigido hacia potenciales decrecientes, o por la repulsión entre cargas de igual signo. 1 ⋅ 10 −6 El Potencial en A a 0,5 m de distancia vale: V A = 9 ⋅ 109 = 18000 V 0,5 1 ⋅ 10−6 = 12857,1 V 0,7 El trabajo realizado por una fuerza conservativa es independiente de la trayectoria e igual a la variación deenergía potencial cambiada de signo. Wcons = −∆E p = −q ⋅ ∆V = −2 ⋅ 10 −6 ⋅ (12857,1 − 18000) = 0,010 J El Potencial en B a 0,7 m de distancia vale: VB = 9 ⋅ 109 socamele.doc Luis Ortiz de Orruño pg 8 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 30.Dos pequeñas esferas iguales, de 5 N de peso cada una, cuelgan de un mismo punto fijo mediante dos hilos idénticos, de 10 cm. de longitud y de masa despreciable. Si se suministra a cada una de estas esferas una carga eléctrica positiva de igual cuantía se separan de manera que los hilos forman entre si un ángulo de 60º en la posición de equilibrio. Calcular: a) la tensión en el hilo. b) El valor de la fuerza electrostática ejercida entre las cargas de las esferas en la posición de equilibrio. c) El valor de la carga de las esferas. Datos: Constante de la ley de Coulomb K = 9.109N.m2.C-2 (Madrid 97) Dibujamos las fuerzas que actúan sobre una de las esferas Como la esfera se encuentra en equilibrio, descomponiendo la tensión en las componente horizontal y vertical y planteando la ecuaciones: 5 = 5,77 N En el eje de las Y: 5 = T cos 30; T = cos 30 5 sen 30 = 2,88 N El eje de las X La Fuerza de repulsión eléctrica (Coulomb) F = T sen 30 = cos 30 La distancia entre las dos cargas: R = 2 ⋅ 0,10 ⋅ sen 30 = 0,10 m Aplicando la ley de Coulomb: F = K socamele.doc qQ r 2 ; 2,88 = 9 ⋅10 9 q2 (0,1) 2 ; luego q =1,79 10–6 C Luis Ortiz de Orruño pg 9 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 32.a) Explica el concepto de potencial eléctrico. ¿Qué potencial eléctrico crea una carga puntual? Dibuja sus superficies equipotenciales. (1 p.) b) Considera dos cargas puntuales fijas q1 = 1 µC y q2 = –2 µC separadas una distancia L = 30 cm. Determina la distancia a q1 del punto sobre la recta que une ambas cargas donde el potencial eléctrico es nulo. ¿Es también nulo allí el campo eléctrico? (1,5 p.) Zaragoza Junio 99 Vtotal = 0 = k 1 ⋅10 −6 − 2 ⋅10 −6 +k x 0,3 − x ; 1 2 = x 0,3 − x ; x = 0,1m No, es imposible, las direcciones y sentidos de los campos creados tienen la misma dirección y sentido. socamele.doc Luis Ortiz de Orruño pg 10 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 33.Un electrón con energía cinética inicial 100 eV penetra en la región sombreada de la figura, de anchura d = 10 cm, donde se sabe que existe un campo eléctrico uniforme. Se observa que el electrón atraviesa dicha región sin desviarse de su trayectoria rectilínea inicial, pero su velocidad a la salida es la mitad de la inicial. Calcula: a) La velocidad inicial v. del electrón. (1 p.) b) El módulo y orientación del campo eléctrico dentro de esa región. (1 p.) e = 1,6-19 C ; me = 9,1 10-31 kg. Zaragoza Junio 99 S 1 eV es la energía que adquiere 1 electrón bajo una diferencia de potencial de 1 Voltio Julio 1eV = 1,6 ⋅10 −19 C ⋅ 1 = 1,6 ⋅10 −19 J C La energía del electrón es cinética: 1,6 ⋅10 −19 J 1 100eV = 9,1 ⋅10 −31 ⋅ v 2 ; v = 5,93 106 m/s 1eV 2 La fuerza eléctrica: F = qE=ma Por cinemática: Como la aceleración es constante v 2 = v 02 + 2 ⋅ a ⋅ e ; v 02 3 − v 02 − v 02 aplicándolo a nuestro caso: = 1,31 ⋅ 1014 ms − 2 = 4 = v 02 + 2 ⋅ a ⋅ e ; a = 4 2e 2 ⋅ 0,1 4 v 02 El campo eléctrico: E = ma 9,1 ⋅ 10 −31 ⋅ 1,31 ⋅ 1014 = = 745,1 N / C q 1,6 ⋅ 10−19 Por energías: W = F ⋅ E ⋅ cos ϕ = ∆Ec 1 v q ⋅ E ⋅ 0,1 ⋅ cos180 = m 0 2 2 − 1,6 ⋅ 10−19 ⋅ E ⋅ 0,1 = socamele.doc 2 − 1 mv02 = 1 − 4 mv02 2 8 ( 3 9,1 ⋅ 10− 31 5,9 ⋅ 106 8 ) 2 ; E = 742,43 N/C Luis Ortiz de Orruño pg 11 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 36.Dos cargas en reposo de 4 µC y 2 µC están situadas, la primera en el origen de coordenadas, y la segunda, a 200 cm de la primera, sobre el semieje positivo de eje OX. Calcula: a) La intensidad del campo eléctrico en el punto de coordenadas (1, 1) en el vacío (las coordenadas están dadas en metros). b) el potencial en dicho punto c) El trabajo realizado para llevar una carga de –5 mC desde el punto (1,1) al (–3,5) r 4 ⋅10 −6 a) E 4 = 9 ⋅10 9 = 18000 N / C ( 2)2 r r r r r E 4 = 18000(cos 45 ⋅ i + sen 45 ⋅ j ) = 12728i + 12728 j r 2 ⋅10 −6 E 2 = 9 ⋅10 9 = 9000 N / C ( 2)2 r r r r r E 4 = 9000(cos 45 ⋅ (−i ) + sen 45 ⋅ j ) = −6364i + 6364 j r r r r r El campo total E total = E 4 + E 2 = 6364i + 19092 j N / C b) El potencial en A: V A = 9 ⋅10 9 V B = 9 ⋅10 9 (+4 ⋅10 −6 ) 34 + 9 ⋅10 9 (+4 ⋅10 −6 ) 2 (+2 ⋅10 −6 ) 50 + 9 ⋅10 9 (+2 ⋅10 −6 ) 2 = 25456 + 12728 = 38184 V = 6174 + 2546 = 8720 V El trabajo para llevar la carga de A a B W AB = −∆E p = −q ⋅ ∆V = −(−5 ⋅10 −3 )(8720 − 38184) = −147,3 J socamele.doc Luis Ortiz de Orruño pg 12 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 37.Dadas dos cargas de –30 µC en (0,-1) y 20 µC en (0,2). Calcular, en la línea recta que une los dos puntos, la posición de un punto P en el que: a) La intensidad de campo sea cero. b) El potencial sea cero. En P es imposible, aun siendo los vectores de sentido contrario, el módulo de E- será siempre mayor que E+ , al tener mas carga y mas cercano que la carga positiva En Q es imposible por que los dos vectores tiene el mismo sentido. En R si que puede ser, llamando x a la distancia entre la carga de +20 y el punto R : E+ = E−6 20 30 20 ⋅10 −6 9 30 ⋅ 10 = 9 ⋅10 9 = 9 ⋅ 10 sacando la raíz de los dos miembros ; x = 13,35 m 2 2 x 3 + x x (3 + x ) en coordenadas la posición es: (0;15,35) b) El potencial puedes ser cero en Q, llamando x a la distancia entre la carga de –30 µC y el punto Q : (−30 ⋅10 −6 ) (+20 ⋅10 −6 ) VQ = 9 ⋅10 9 + 9 ⋅10 9 = 0 ; x = 1,8 m x x En R también puede ser cero, llamando x a la distancia entre la carga de 20 µC y el punto R (−30 ⋅10 −6 ) (+20 ⋅10 −6 ) V R = 9 ⋅10 9 + 9 ⋅10 9 =0;x=6m x 3+ x socamele.doc Luis Ortiz de Orruño pg 13 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 43.Cuatro cargas eléctricas de 10,0 nC, -12,0 nC, 20,0 nC y 25,0 nC están colocadas en los vértices de un cuadrado de lado l = 1,2 m. Encuentra el potencial eléctrico en el centro del cuadrado. Dato: Constante de Coulomb = 8,99 109 N m2 C–2 Baleares 99 La diagonal del cuadrado vale: d = 1,2 2 + 1,2 2 1,697 m El potencial total: Vtotal = k ( ) − 12 ⋅10 −9 10 ⋅10 −9 20 ⋅10 −9 25 ⋅10 −9 +k +k +k 1,697 1,697 1,697 1,697 2 2 2 2 = k ⋅2 (10 − 12 + 20 + 25) ⋅10 −9 = 455,6 V 1,697 socamele.doc Luis Ortiz de Orruño pg 14 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 46.En el espacio comprendido entre dos láminas planas y paralelas con cargas iguales y opuestas existe un campo eléctrico uniforme. Un electrón abandonado en reposo sobre la lámina cargada negativamente llega a la superficie de la lámina opuesta, situada a 2 cm de distancia de la primera, al cabo de 1,5 10–8 s Despreciando los efectos gravitatorios, calcula: a) La intensidad del campo eléctrico entre las láminas. b) La velocidad con que llega el electrón a la segunda lámina. c) La diferencia de potencial entre las láminas. Datos: Carga e 1,6 10-19 C ; Masa del electrón: me =9,10 10–31 kg. País Vasco 99 a) La fuerza eléctrica Felec = q ⋅ E = m ⋅ a ; como la aceleración es constante el espacio recorrido en un m.u.a. será e= ( 1 2 1 qE 2 1 1,6 ⋅10 −19 ⋅ E at = t ; 2 ⋅10 − 2 = 1,5 ⋅10 −8 2 2 m 2 9,1 ⋅10 −31 b) Por cinemática: v = v 0 + at = Por energías: (Ep)eléctrica = Ec; 1,6 ⋅10 −19 ⋅ 20,22 = socamele.doc ) 2 ; E = 1011 N/C q⋅E t = 2,67 ⋅10 6 m / s m 1 ∆V q ⋅ ∆V = mv 2 como E = − 2 ∆r ; 1011 = ∆V ; ∆V = 20,22 V ; 0,02 1 9,1 ⋅10 −31 v 2 ; v = 2,67 106 m/s 2 Luis Ortiz de Orruño pg 15 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 47.a) Explica el concepto de energía potencial eléctrica. ¿Qué energía potencial eléctrica tiene una partícula de carga q2 situada a una distancia r de otra de carga ql? (1,5 p.) b) Una partícula de carga q1 = 0,1 µC está fija en el vacío. Se sitúa una segunda partícula de carga q2 = 0,5 µC y masa m = 0,1 g a una distancia r = 10 cm de la primera. Si se suelta q2 con velocidad inicial nula, se moverá alejándose de ql. ¿Por qué? Calcula su velocidad cuando pasa por un punto a una distancia 3r de ql. (1,5 p.) Constante de Coulomb: K = l/(4π0) = 9 109 N m2 C–2. Zaragoza Junio 2000; 7,75 m/s b) Son cargas de igual signo y se repelen y/ó su energía potencial es positiva El potencial en A creado por la carga q1 vale: 0.1 ⋅10 −6 V A = 9 ⋅10 9 = 9000 V 0,1 El potencial en B creado por la carga q2 vale: 0.1 ⋅10 −6 V B = 9 ⋅10 9 = 3000 V 0,3 Como el campo es conservativo el trabajo es independiente de la trayectoria y depende solo de una función Energía Potencial. W AB = −∆E p = − q∆V = − q 2 (V B − V A ) En cualquier caso el trabajo es igual a la variación de la energía potencial. 1 W AB = ∆E c = mv 2 − 0 2 1 − 0,5 ⋅10 − 6 3 ⋅10 3 − 9 ⋅10 3 = 0,1 ⋅10 −3 ⋅ v 2 ; v = 60 m / s = 7,75 m / s 2 ( socamele.doc ) Luis Ortiz de Orruño pg 16 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 58.Un dipolo eléctrico está formado por dos cargas puntuales de 2 µC y – 2 µC distantes entre sí 6 cm. Calcula el campo y el potencial eléctrico: a) En un punto de la mediatriz del segmento que las une, distante 5 cm de cada carga b) En un punto situado en la prolongación del segmento que las une y a 2 cm de la carga positiva. r r Dato: K = 9 109 S.I. Comunidad Valenciana 2000; 8,64 ⋅ 106 i N / C ; 0 V ; − 106 i ; 675000 V senϕ = 4 3 ; cos ϕ = 5 5 r N 2 ⋅ 10 −6 E1 = 9 ⋅ 109 = 7,2 ⋅ 106 C (0,05)2 r 3r 4r E1 = 7,2 ⋅ 106 i + 7,2 ⋅ 106 j 5 5 r r 3 4 r E2 = 7,2 ⋅ 106 i + 7,2 ⋅ 106 − j 5 5 r r rN 3 ETotal = 2 ⋅ 7,2 ⋅ 106 i = 8,64 ⋅ 106 i C 5 ( ) El potencial V = 9 ⋅ 109 + 2 ⋅ 10 −6 − 2 ⋅ 10 −6 + 9 ⋅ 109 = 0V 0,05 0,05 b) r r r N N 2 ⋅ 10−6 E1 = 9 ⋅ 109 = 4,5 ⋅ 106 ; E1 = 4,5 ⋅ 106 − i 2 C C (0,02) r 2 ⋅10 −6 N = 2,81 ⋅10 6 E 2 = 9 ⋅10 9 ; 2 C (0,08) r r N E1 = 2,81 ⋅ 10 6 i C r r r rN ETotal = E1 + E 2 = 42,19 ⋅ 10 6 i C ( ) () El potencial V = 9 ⋅10 9 socamele.doc + 2 ⋅10 −6 − 2 ⋅10 −6 + 9 ⋅10 9 = 675000 V 0,02 0,08 Luis Ortiz de Orruño pg 17 de 18 www.lortizdeo.tk mailto:lortizdeo@hotmail.com I.E.S. Francisco Grande Covián 09/07/2003 Campo Eléctrico Física 2ªBachiller 59.a) Explica el concepto de campo eléctrico creado por una o varias partículas cargadas. (1 p.) b) Dos partículas con carga q = 0,8 µC, cada una, están fijas en el vacío y separadas una distancia d = 5 m. Determina el vector campo eléctrico que producen estas cargas en el punto A, que forma un triángulo equilátero con ambas. (1 p.) c) Calcula el campo y el potencial eléctricos en el punto medio entre las cargas, B. (1 p.) Constante de Coulomb: K = 1 (4πε ) = 9 ⋅10 9 N m 2 C −2 Zaragoza Junio 2001; 0 r N 498,8 j C ; 0; 5760 V b) Como las cargas son positivas los campos son en la dirección de las rectas que unen r 0,8 ⋅ 10 −6 N carga y punto y sentido salientes, el módulo E1 = 9 ⋅ 10 9 = 288 2 C 5 r r r E1 = 288 cos 60 i + 288sen60 j r r r E 2 = 288 cos 60 − i + 288sen60 j r r r N Sumando ET = 2 ⋅ 288sen60 j = 498,8 j C c) En B los campos eléctricos son de igual módulo, dirección y sentido contrario, r luego el campo total es cero. ET = 0 ( ) El potencial V = 9 ⋅ 10 9 socamele.doc 0,8 ⋅ 10 −6 0,8 ⋅ 10 −6 + 9 ⋅ 10 9 = 5760 V 2,5 2,5 Luis Ortiz de Orruño pg 18 de 18