¿Quién quiere ser mi socio?

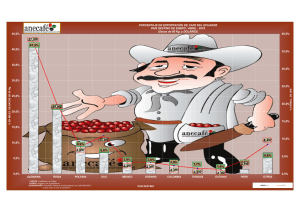
UNIDA
D2
SESIÓN
13
TERCER GRADO
¿Quién quiere ser mi socio?
En esta sesión, los niños y las niñas
aprenderán a resolver problemas
aditivos usando la propiedad
asociativa de la adición.
Antes de la sesión
Revisa la página 43 del libro Matemática 3.
Complementa este trabajo leyendo
información sobre la propiedad asociativa de
la adición.
MATERIALES O RECURSOS A UTILIZAR
Cuadernos y lápices.
Semillas, botones, tapitas, etc.
Bolsas de plástico.
Pizarra y tizas de colores.
Libro Matemática 3 (pág. 43).
Ministerio
71
COMPETENCIA(S), CAPACIDAD(ES) E INDICADORES
A TRABAJAR EN LA SESIÓN
COMPETENCIA
CAPACIDADES
INDICADORES
Plantea y resuelve
problemas con
cantidades y
magnitudes
que implican la
construcción y
uso de números
y operaciones,
empleando diversas
representaciones
y estrategias para
obtener soluciones
pertinentes al contexto.
Comunica y representa el
significado de los números
y operaciones en la
resolución del problema, a
través de la socialización,
usando notación y
terminología apropiadas.
Utiliza algoritmos
convencionales para
sumar cantidades de
hasta dos cifras (aplicando
la propiedad asociativa),
con soporte concreto y
simbólico.
Elabora y usa estrategias,
y procedimientos que
involucran relaciones
entre el número y sus
operaciones, haciendo uso
de diversos recursos.
Describe paso a paso
lo que hizo al resolver
problemas simples aditivos
con cantidades de hasta
dos cifras.
Momentos de la sesión
Inicio
15
minutos
Pide a los estudiantes que muestren la tarea encargada en la sesión
anterior (cinco operaciones aplicando la propiedad conmutativa de la
adición). Indica que, formados en parejas, intercambien sus cuadernos
y se corrijan entre ellos. Luego, propón que algunos(as) salgan a
la pizarra voluntariamente a escribir sus ejercicios y permite que los
demás hagan preguntas sobre las dudas que tengan.
Recoge los saberes previos de los niños y las niñas sobre la idea de
asociarse. Pregunta: ¿saben el significado de la palabra “socio”? ¿qué
significa asociar?, ¿para qué se asocian las personas? Se espera
respuestas como las siguientes: los socios son personas que realizan
una misma actividad, por ejemplo pueden juntar su dinero para hacer
negocio, asociar quiere decir reunir, juntar.
Comunica el propósito de la sesión: hoy aprenderán a resolver
problemas aditivos usando una propiedad de la adición.
Revisa junto con los estudiantes algunas normas de convivencia que los
ayudarán a trabajar en equipo. Indica que hoy reforzarán el valor del
aliento al compañero o a la compañera que se esfuerza para mejorar
sus aprendizajes.
72
Desarrollo
60
Organiza a los estudiantes en grupos y plantea la siguiente situación
problemática (léela en voz alta):
minutos
Eduardo tiene tres sacos de papas de 23 kg, 40 kg y 17
kg, que llevará a la feria para su venta. Si desea llevar
la carga en dos partes, ¿cuántos kilogramos puede llevar
cada día?, ¿de cuántas formas podrá acomodar los sacos
de papas? , ¿cuántos kilogramos de papa está llevando
para vender?
Formula algunas preguntas para asegurar la comprensión del problema:
¿qué quiere hacer Eduardo?, ¿puede llevar los tres sacos de papas a la
vez?, ¿puede hacer tres viajes?, ¿por qué? Las preguntas están dirigidas
a comprender que Eduardo tiene que hacer dos acomodos diferentes
de los tres sacos: dos y uno o uno y dos.
Orienta a cada grupo a fin de buscar la estrategia que les permita
resolver el problema. Entrégales material para contar (semillas, botones,
tapitas, etc.) y bolsas plásticas para representar los sacos. También
bríndales la opción de dramatizar el problema.
Guía a los niños y a las niñas a elegir una estrategia y oriéntalos en la
aplicación. Pregunta:
Si el primer día Eduardo lleva un saco y el segundo día lleva dos,
¿cuál es la operación que representa esta situación?
Obtendrás respuestas como la siguiente:
Primer día: 23 kg
Segundo día: 40 + 17
Operación: 23 + 40 + 17
Señala que los paréntesis
sirven para agrupar
cantidades e indican lo que
se debe sumar primero.
Aquí debes introducir el
uso de los paréntesis ( ),
necesarios para separar una
operación de otras.
Hazlo en rojo e indícalo así:
23 + (40 + 17) = 23 + 57 = 80
73
Invita a que un representante de cada grupo exponga otras
combinaciones diferentes a la presentada. Obtendrás las siguientes:
40 + (23 + 17) = 40 + 40 = 80
17 + (40 + 23) = 17 + 63 = 80
Pregunta: ¿cómo son los resultados en los tres casos?
Quizá algunos grupos presenten opciones como estas:
40 + (17 + 23) o 17 + (23 + 40) o 23 + (17 + 40)
De ser el caso, indica que no se trata de acomodos diferentes, ya que es
lo mismo que el segundo día lleve 23 + 17 = 40 o que lleve 17 + 23 = 40.
Cuando se realiza una adición de tres o más números,
la suma siempre es la misma independientemente del
agrupamiento que se realice.
También es posible que presenten opciones como estas:
(17 + 23) + 40 o (23 + 40) + 40 o (17 + 40) + 23
Menciona a los estudiantes que tres sumandos pueden ser acomodados
o asociados de tres formas diferentes y que en todos los casos el
resultado será el mismo.
Plantea preguntas respecto a la solución del problema: ¿en qué nos
ayudaron los paréntesis?, ¿de cuántas formas se pudo combinar los
pesos de los tres sacos de papas en dos días?, ¿cuál es la respuesta a
la última pregunta del problema? Se espera que respondan:
Los paréntesis nos ayudaron a diferenciar la carga del día que
Eduardo llevó dos sacos.
Se encontraron seis formas diferentes.
Eduardo está llevando 80 kg de papa.
Para formalizar el conocimiento, señala que lo que han aplicado los
estudiantes es la propiedad asociativa de la adición, mediante la cual
tres o más sumandos se pueden asociar de diferentes maneras, y el
resultado siempre será el mismo. Recuerda que los términos de la
adición son dos: sumandos y suma o total.
Plantea otras situaciones
Pide a cada grupo que resuelva la actividad 2 de la página 43 del libro
Matemática 3 (indica ignorar los recuadros con números). Oriéntalos
para que observen que los números dentro de los paréntesis pueden ir
primero, así: (213 + 107) + 50 pero también pueden ir de otras formas.
Invita a dos o tres grupos a exponer en la pizarra sus alternativas
de solución y permite que sus compañeros y compañeras puedan
comentar el trabajo.
74
Cierre
10
minutos
Promueve un diálogo con los niños y las niñas sobre lo aprendido hoy
e invítalos a que expresen sus sentimientos frente a ello (satisfacción,
frustración por no entender, entusiasmo frente a los retos superados,
etc.). Luego, comenta que cada cual tiene un ritmo diferente de
aprendizaje y que todos están para ayudarse mutuamente.
Felicítalos por los logros obtenidos y propón que los estudiantes elijan al
compañero o a la compañera que se esforzó más, brindándole un gran
aplauso.
75