ω N N 0.1 = y al final de la línea de transmisión hay otro
Anuncio
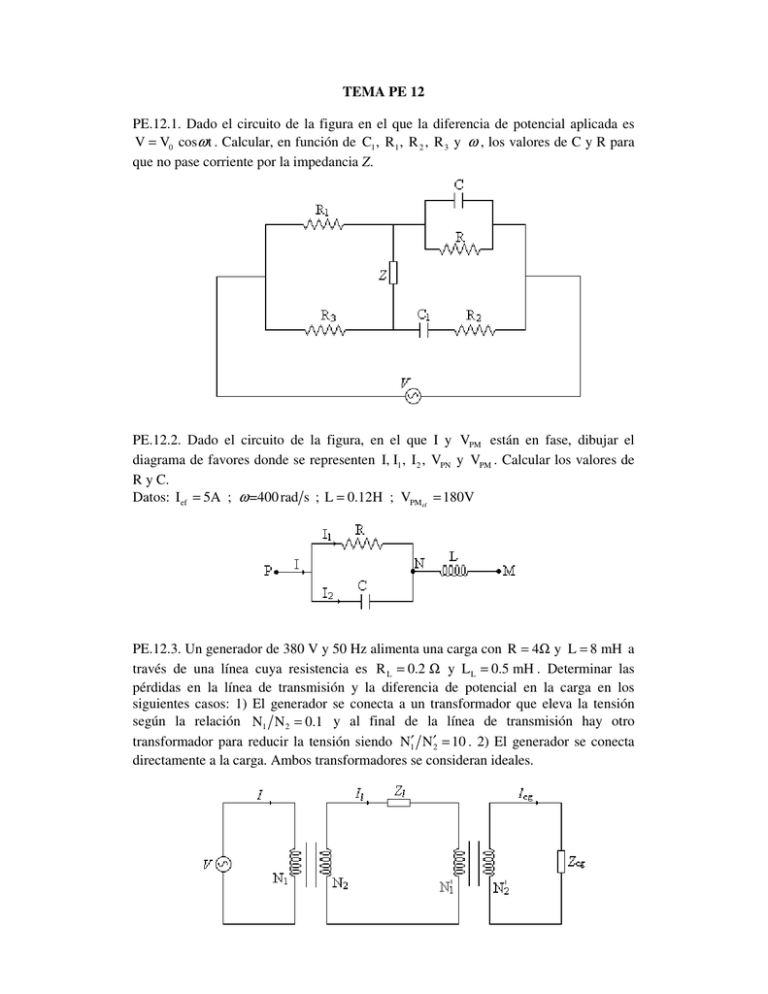
TEMA PE 12 PE.12.1. Dado el circuito de la figura en el que la diferencia de potencial aplicada es V = V0 cosω t . Calcular, en función de C1 , R1 , R 2 , R 3 y ω , los valores de C y R para que no pase corriente por la impedancia Z. PE.12.2. Dado el circuito de la figura, en el que I y VPM están en fase, dibujar el diagrama de favores donde se representen I, I1 , I2 , VPN y VPM . Calcular los valores de R y C. Datos: Ief = 5A ; ω =400 rad s ; L = 0.12H ; VPMef = 180V PE.12.3. Un generador de 380 V y 50 Hz alimenta una carga con R = 4Ω y L = 8 mH a través de una línea cuya resistencia es R L = 0.2 Ω y L L = 0.5 mH . Determinar las pérdidas en la línea de transmisión y la diferencia de potencial en la carga en los siguientes casos: 1) El generador se conecta a un transformador que eleva la tensión según la relación N1 N 2 = 0.1 y al final de la línea de transmisión hay otro transformador para reducir la tensión siendo N1′ N′2 = 10 . 2) El generador se conecta directamente a la carga. Ambos transformadores se consideran ideales. PE12.4. Un ingeniero informático trabaja en el circuito integrado de una placa base de un ordenador, la cual es alimentada por un generador de corriente alterna de 80 V y a través de un pequeño circuito en el que hay dos impedancias Z1=7+j5 y Z2=3+j4 en paralelo, como muestra la figura. Ayuda al ingeniero a analizar este pequeño circuito encontrando el valor de los elementos (impedancias) y magnitudes (corrientes) que lo conforman, así como el desfase existente entre la intensidad I y la tensión de alimentación. PE12.5. El último becario llegado a una prestigiosa empresa de hardware recuerda haber estudiado durante la carrera algo en relación con el factor de potencia, pero no lo recuerda nada bien. Ayúdale a refrescar su memoria y a resolver el siguiente problema que le ha propuesto su nuevo jefe de departamento: La potencia que disipa la impedancia Z1 vale 100w y el valor de la potencia media que absorbe la impedancia Z2 es de 500w, si Z1=4Ω y el módulo de Z2 es 30Ω, se pide: a) Potencia total generada por la fuente ε. b) Factor de potencia. PE.12.6. En el circuito de la figura, se pide: 1) Equivalente Thevenin entre los puntos A y B. 2) Calcular la impedancia que hay que conectar entre A y B para que reciba la máxima potencia del circuito y dicha potencia. R 1 = 3Ω ; R 2 = 4Ω ; R 3 = 6Ω C1 = 637 µ F L1 = 31.8mH ; L 2 = 22.3mH ε1 = 2 0º V ; ε 2 = 5 45º V ε 3 = 4 90º V I1 = 2 30º A f = 50Hz PE.12.7. En el circuito de la figura se sabe que la potencia máxima que se puede transferir a la impedancia situada entre A y B es de 50w y que el desfase de VA − VB a circuito abierto es de 0º. Determinar con estas condiciones el valor polar de I. f = 50Hz ; ε = 10 90º V R 1 = 2Ω ; R 2 = 3Ω R 3 = 5Ω ; R 4 = 1Ω C1 = 3.2mF C 2 = 0.64mF L1 = 9.5mH L 2 = 19mH PE.12.8. En el circuito de la figura sabemos que si Z L vale 3.091 −2.72º Ω se produce la máxima transferencia de potencia a dicha impedancia de valor P = 4.13w . También se sabe que la fase a circuito abierto de VA − VB es de -23º. Con estos datos calcular L1 e I . ε = 10 0º V R 1 = 5Ω R 2 = 8Ω C1 = 1061µ F L 2 = 9549 µ H f = 50Hz PE.12.9. Conociendo en la red de la figura que la máxima potencia consumida por la impedancia Z ′ situada entre A y B es de 22.5 w y que la fem de Thevenin de la red sin la impedancia Z ′ vale ε TH 27.26 o V. Determinar: a) ε 2 b) La potencia reactiva en L1. I 1 = 2 30º A ; ε 1 = 5 45º V L1 = 31.8mH ; C1 = 637 µF R 1 = 3Ω ; R 2 = 4Ω Z ′ = 2.52 24.89º Ω f = 50Hz PE.12.10. En el circuito de la figura, sabiendo que las potencias disipadas en las resistencias R2 y R3 suman 17 w, se pide: a) Valor polar de I ; b) Valor de R3 ; c) Valor de L1 f = 50 Hz ε = 14.14 -45º I1 = 7.21 33.7º I 2 = 2 0º L2 C1 C2 R1 R2 R4 = 6.4 mH = 1591 µF = 265 µF = 10 Ω =1Ω = 3Ω PE.12.11. En el circuito de la figura, determinar el equivalente Norton entre los puntos A y B. Datos: f = 50Hz ; ε 1 = 2 0º V ; ε 2 = 5 45º V ; I 1 = 2 30º A ; C1 = 637 µF ; L1 = 31.8mH ; L 2 = 22.3mH R 1 = 3Ω ; R 2 = 4Ω PE.12.12. En la red de la figura se pide calcular la potencia disipada en R 4 , el valor de R1 y la ddp en bornes de la fuente de corriente. Datos: ε1 = 14.14 −45º V ; I1 = 7.21 33.7º A ; I 2 = 2 0º A ; R 2 = 4Ω ; R 3 = 3Ω R 4 = 1Ω ; C1 = 265µ F ; C2 = 1591µ F ; L1 = 31.8mH ; L 2 = 6.4mH ; f = 50Hz PE.12.13. En la red eléctrica de la figura, además de los datos que se proporcionan, se sabe que ε TH = 9.71 −106.57º V . Se pide a) Valor de ε 2 ; b) la impedancia a colocar entre A y B para que se produzca la máxima transferencia de potencia y el valor de la potencia. Datos: I 3 = 2 45º A ; ε1 = 10 0º V ; f = 50 Hz ; R 1 = 20 Ω ; R 2 = 30 Ω C1 =265µ F ; C2 = 1591 µ F ; C3 = 318.3 µ F ; L1 = 15.91 mH ; L 2 = 6.4 mH PE.12.14. Dado el circuito de la figura, determinar: a) La intensidad de corriente I. B) La impedancia que habría que colocar entre A y B para que se transfiera la máxima potencia. Calcular, también, dicha potencia. C1 = 800 µF C 2 = 300 µF C 3 = 500 µF L1 = 20 mH L 2 = 12 mH R 1 = 10 Ω R 2 = 20 Ω f = 50 Hz PE.12.15. Sabiendo que la d.d.p. entre A y B es VA − VB = 48.35 − 110.49º V , determinar: 1) El valor de I. 2) Potencia reactiva en C1 y potencia activa en R 4 . f = 50Hz ; ε = 40 90º V C1 = 1591µF ; C 2 = 637µF L1 = 31.8mH ; L 2 = 22.3mH R 1 = 3Ω ; R 2 = 4Ω R 3 = 7Ω ; R 4 = 10Ω PE.12.16. En la red eléctrica de la figura se pide a)El valor de Z que hay que poner entre A y B para que se transfiera la máxima potencia b)Valor que marcaría el amperímetro, una vez colocada la Z obtenida en el apartado anterior. Datos: R 1 = 4Ω ; R 2 = 1Ω ; C1 =265µ F ; C 2 = 159 µ F ; L1 = 31.8mH ; L 2 = 6.4mH ; L3 = 3.18mH ε = 14.14 −45º V ; I = 2 0º A ; f = 50Hz









