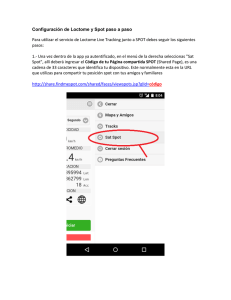
Interacción entre los mercados eléctricos a plazo y los

UNIVERSIDAD PONTIFICIA COMILLAS
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA (ICAI)
INSTITUTO DE POSTGRADO Y FORMACIÓN CONTINUA
MÁSTER EN GESTIÓN TÉCNICA Y ECONÓMICA EN EL SECTOR ELÉCTRICO
Tesis de máster
Interacción entre los mercados eléctricos a plazo y
los mercados eléctricos al contado.
Estudio del comportamiento estratégico
de los generadores.
Autor: Pilar Vázquez Martínez
Director: Dr. Íñigo Rupérez García del Carrizo
Madrid, 2008
Índice
1. Introducción
5
1.1 Objetivos de la tesis de máster
6
1.2 Organización del documento
6
2. El mercado eléctrico
2.1 Organización del mercado eléctrico
2.1.1 Sistemas tradicionales fuertemente regulados
2.1.2 Mercados con competencia perfecta
2.1.3 Mercados con competencia imperfecta
9
10
10
12
17
2.2 Mercados spot y mercados a plazo
18
2.3 Modelos de planificación de la operación en un mercado en competencia
imperfecta
20
2.3.1 Organización jerárquica de la planificación
2.3.2 Tipos de modelos de planificación
2.3.3 Modelos clásicos de equilibrio
2.4 Modelos del comportamiento estratégico en los mercados a plazo
3. Modelo de una etapa
3.1 Metodología basada en el problema de complementariedad
3.1.1 Planteamiento
3.1.2 Descripción
20
21
23
26
29
30
30
31
3.2 Planteamiento del modelo
33
3.3 Formulación del problema del equilibrio del mercado
35
3.3.1 Formulación del problema de optimización de cada empresa
3.3.2 Construcción del lagrangiano del problema de optimización de cada
empresa
3.3.3 Obtención de las condiciones de optimalidad de cada empresa
35
37
37
3.3.4 Formulación del equilibrio del mercado como un problema mixto de
complementariedad
42
3.4 Equilibrio de Cournot
43
3.5 Conclusiones
44
4. El modelo de Allaz y Vila
47
4.1 Planteamiento
48
4.2 Formulación del modelo
50
4.2.1 Mercado spot
4.2.2 Mercado a plazo
50
54
4.3 Análisis de los resultados
58
4.4 Conclusiones
65
5. Generalización del modelo de Allaz y Vila
67
5.1 Planteamiento
68
5.2 Formulación del modelo
68
5.2.1 Mercado spot
5.2.2 Mercado a plazo
68
81
5.3 Análisis de los resultados
91
5.4 El coste de producción
95
5.5 Formulación general del modelo como un problema de equilibrio con
restricciones de equilibrio
97
5.6 Conclusiones
97
6. Efectos dinámicos en el comportamiento estratégico de los agentes
101
6.1 Planteamiento
102
6.2 Análisis del comportamiento de los agentes en mercados sucesivos
104
6.3 Conclusiones
110
7. Conclusiones
113
Referencias
117
Los resultados, conclusiones y puntos de vista reflejados en este documento son
exclusivamente los de su autora y no comprometen ni obligan en modo alguno a
ninguna otra empresa, persona o entidad.
1
Introducción
En los últimos 20 años, muchos de los mercados eléctricos han sido liberalizados para
funcionar de forma competitiva con el objeto de incentivar la toma de decisiones más
eficientes. Este objetivo se consigue plenamente en un entorno de competencia perfecta
pero, en estos momentos, existen múltiples mercados en los que el nivel de
competencia no es tan alto. Por tanto, para el estudio de los mercados eléctricos reales
se necesitan modelos de equilibrio que reflejen que no se verifican las condiciones de
competencia perfecta, sino que las decisiones de las empresas sí pueden influir en los
precios.
La gran mayoría de los modelos de este tipo no tienen en cuenta la existencia de
mercados a plazo, y sólo en los últimos años se han desarrollado varios tipos de
modelos para representar el comportamiento de los agentes que tienen la posibilidad
de operar tanto en un mercado spot como en un mercado a plazo. Sin embargo, los
mercados eléctricos de numerosos países –Francia, Alemania, Holanda, entre otros–
cuentan con mercados a plazo en los que se negocian importantes volúmenes de
energía. Incluso en España, que hasta hace poco constituía una excepción en este
sentido, se han tomado recientemente diversas medidas encaminadas a fomentar la
contratación a plazo de los agentes del mercado.
Los mercados a plazo son herramientas eficaces para gestionar el riesgo de las
empresas. Así, su utilidad principal consiste en reducir los efectos de la volatilidad de
los precios que reciben los agentes. Los precios de los mercados de corto plazo son
muy volátiles, ya que cualquier variación en alguno de los factores que intervienen en
la formación del precio, como, por ejemplo, la demanda de energía de los
consumidores o el precio de los combustibles empleados para generar electricidad, se
refleja de manera casi inmediata en el precio de la energía. Mediante la negociación de
5
1 Introducción
contratos a plazo, los agentes pueden asegurar la venta de una cierta cantidad a un
precio determinado a lo largo de un periodo futuro y gestionar, así, su riesgo de precio.
Sin embargo, la existencia de un mercado a plazo podría influir en el comportamiento
estratégico de los agentes cuando éstos toman sus decisiones de producción en el
mercado spot. Surge, por tanto, la necesidad de estudiar si los agentes modifican sus
estrategias de oferta en los mercados de corto plazo cuando contratan parte de su
energía.
1.1 Objetivos de la tesis de máster
Esta tesis de máster pretende realizar un análisis teórico de la posible influencia que
puede tener los mercados a plazo en el comportamiento de los agentes que operan en
un mercado spot. Este problema, aún sin resolver, está siendo objeto de una intensa
actividad investigadora. El objetivo de la tesis de máster es profundizar en la
interacción existente entre los mercados eléctricos a plazo y los mercados eléctricos al
contado y, en particular, en los efectos que la contratación a plazo puede tener sobre las
estrategias de producción de las empresas.
Para ello, se partirá del modelo descrito en Allaz y Vila (1993), que ha sido en buena
medida el trabajo pionero en este campo y ha dado lugar a numerosos artículos de
investigación, analizando las hipótesis y resultados de este modelo. A continuación, se
desarrollará un modelo original que permite representar de una manera más realista
los mercados eléctricos existentes. Aparecen, entonces, algunos efectos que modifican
drásticamente las conclusiones del modelo de Allaz y Vila.
1.2 Organización del documento
La tesis de máster está organizada como se describe a continuación.
En el capítulo 2 se estudia cómo la liberalización del sector eléctrico ha modificado
profundamente los mecanismos de gestión económica y estratégica de las empresas, y
se presentan diferentes alternativas en el modelado de la operación de una empresa en
un mercado en competencia imperfecta.
El capítulo 3 presenta una metodología basada en el problema de complementariedad
que permite resolver el problema del equilibrio de un mercado en competencia. Esta
metodología se aplica a un modelo de una etapa en el que no se considera la existencia
de mercados a plazo para realizar una primera aproximación al problema de la
representación de un mercado eléctrico en competencia imperfecta.
En el capítulo 4 se describe el modelo desarrollado en Allaz y Vila (1993), que define el
punto de partida del análisis que se realizará en esta tesis de máster, estudiando
detalladamente los resultados obtenidos y sus implicaciones.
6
1.2 Organización del documento
El modelo que se presenta en el capítulo 4 no permite representar un caso general, ya
que las hipótesis adoptadas por Allaz y Vila son muy inflexibles en lo que se refiere a
la estructura del mercado y las características de las empresas generadoras. Por este
motivo, el capítulo 5 se dedica al desarrollo de un modelo general basado en el modelo
del capítulo anterior. Esta generalización, que constituye una aportación original de la
tesis de máster, permite aplicar el modelo al estudio de algún mercado eléctrico
general.
En el capítulo 6 se revisan las hipótesis del modelo de Allaz y Vila. Este modelo no
tiene en cuenta la interacción repetida que existe entre los diferentes mercados
eléctricos. Al incorporar la existencia de periodos de negociación futuros, aparecen una
serie de efectos que invalidan las conclusiones de los capítulos anteriores. En concreto,
en este capítulo se desarrolla un modelo original basado en un juego repetido no
colusivo que revela que, cuando se tiene en cuenta que tras cada mercado spot existe un
nuevo mercado a plazo, los resultados de Allaz y Vila se modifican sustancialmente.
Finalmente, el capítulo 7 recoge las conclusiones de la tesis de máster.
7
2
El mercado eléctrico
La organización de la industria eléctrica ha experimentado en las últimas dos décadas
cambios significativos a un ritmo sin precedentes en su historia, con el objeto de
establecer nuevos esquemas regulatorios que permitan pasar desde los sistemas
tradicionales fuertemente regulados a mercados en competencia. El objetivo último de
estas transformaciones consiste en conseguir una mejora de la eficiencia mediante la
introducción de mecanismos de mercado en aquellas actividades que pueden realizarse
en condiciones competitivas, como es el caso del negocio de la generación.
En este nuevo entorno, el análisis y modelado del funcionamiento de los mercados de
generación de electricidad han despertado gran interés tanto en las empresas
productoras como en el regulador. Esto ha dado origen a numerosas publicaciones que
tratan de conjugar el modelado realista del comportamiento estratégico de las
empresas con la representación técnica detallada de la explotación de los medios de
producción.
En este capítulo se analiza el proceso de liberalización del sector eléctrico y se presenta
una revisión de los distintos enfoques y tendencias de modelado propuestos en la
literatura.
9
2 El mercado eléctrico
2.1 Organización del mercado eléctrico
El sector eléctrico se ha considerado tradicionalmente como un monopolio natural
sujeto a una fuerte regulación. Sin embargo, en los últimos 20 años se ha planteado la
posibilidad de introducir competencia en la industria y ya son muchos los sistemas
eléctricos en todo el mundo que se han organizado en torno a un mercado de
generación.
Las características de las actividades del sector eléctrico son muy diversas, tanto en
términos técnicos como económicos, y sólo algunas de ellas se pueden desarrollar en
condiciones de competencia. En concreto, la desregulación es, realmente, desregulación
de la generación y de la comercialización de la energía eléctrica. El transporte y la
distribución son monopolios naturales que siguen estando fuertemente regulados en
todo el mundo. En la mayor parte de los países, eran las mismas empresas las que se
ocupaban de la generación y la distribución, así que la desregulación ha requerido, al
menos, la separación clara dentro de la misma empresa de las diferentes actividades
que incluye el sector. Esta tesis de máster se centra en la actividad de generación de
electricidad.
2.1.1
Sistemas tradicionales fuertemente regulados
Hasta los años 80, la industria eléctrica de todo el mundo estaba formada por empresas
nacionalizadas o empresas privadas, en general muy grandes, fuertemente reguladas.
Existían una serie de factores que explicaban esta situación, pero la principal razón
tenía que ver con la existencia de un monopolio natural. Si el sistema es de pequeño
tamaño, las tecnologías aplicadas a la generación presentan economías de escala, es
decir, el coste total del suministro eléctrico es menor cuando se emplea un único
generador de tamaño, por ejemplo, 100 MW que cuando se usan dos generadores de
50 MW. En estas circunstancias, las centrales de gran tamaño se ven favorecidas y no
tiene ningún sentido intentar que varias empresas compitan entre sí, ya que la solución
más económica consiste en que una única empresa lleve a cabo todas las inversiones y
capture todas las economías de escala. Al crecer el consumo de electricidad y, en
consecuencia, la dimensión del sector, el impacto de las economías de escala se va
reduciendo paulatinamente.
A esto hay que añadir la presencia de economías de coordinación. Si existen regiones
aisladas unas de otras, en cada una de ellas se explotarán las centrales de esa zona de la
mejor forma posible. Sin embargo, si esas regiones están conectadas entre sí, la
explotación debe tener en cuenta todos los generadores para que la operación del
conjunto sea lo más eficiente posible. Plantas generadoras que en su región no eran
utilizadas pueden ser más económicas que otras de otras regiones que sí tenían que
funcionar para ofrecer el suministro de energía a su zona. Al conectarse las regiones
generarán aquéllas antes que éstas, por lo que se consigue una mejor operación del
conjunto del parque eléctrico.
10
2.1 Organización del mercado eléctrico
Con estas condiciones, la organización más adecuada del sistema eléctrico presenta un
enfoque centralizado que permita aprovechar las economías de escala y coordinación.
Esta centralización se ha plasmado de diferentes maneras en la organización del sector
dependiendo del país. Dentro de ellas se pueden distinguir dos formas básicas.
Una primera opción consiste en una única empresa pública que controla
completamente la actividad eléctrica del país. Esta empresa se encarga de decidir las
inversiones necesarias en instalaciones e infraestructuras para adaptarse a las
necesidades de los consumidores, así como de llevar a cabo la operación del sistema.
Las inversiones y los costes de operación se pagan con dinero público. El gobierno a
través de la empresa determina lo que han de pagar los consumidores para disfrutar de
la energía eléctrica. Éste ha sido el sistema adoptado hasta hace pocos años por un
buen número de países en el mundo. Uno de los ejemplos más notables es el caso de
Francia, a través de la empresa Électricité de France.
Una alternativa diferente es la de un sector formado por varias empresas privadas,
pero cuyo comportamiento depende del gobierno. Las decisiones de inversión las
toman las empresas, pero para poder emprender tales inversiones deben solicitar el
permiso del regulador. Si lo obtienen realizan la inversión, que posteriormente es
pagada por la Administración Pública a través de las tarifas. La operación del sistema
es realizada por las propias empresas, bajo supervisión periódica del regulador. Éste
era el modelo empleado en Estados Unidos, entre otros países, hasta mediados de los
años 80.
También es posible que las decisiones de inversión sean responsabilidad del gobierno.
En este caso, en lugar de aprobar las decisiones de las empresas, el gobierno dicta
directamente qué inversiones debe realizar cada una de ellas. Dichas inversiones son
pagadas en último término con dinero público. La operación del sistema también es
decidida de forma centralizada. Del mismo modo, el dinero que reciben las empresas
por su producción de energía es determinado por los gobernantes. Esta alternativa ha
sido la que se ha dado en España hasta el 1 de enero de 1998, donde el Ministerio de
Industria a través del Plan Energético Nacional era el encargado de tomar las
decisiones sobre inversiones referidas al sector eléctrico, que se remuneraban por
medio del Marco Legal Estable. Igualmente, una empresa especializada, Red Eléctrica
de España, era la encargada desde 1984 de tomar las decisiones sobre la operación del
sistema, y los costes incurridos por las empresas eran de nuevo sufragados por medio
del Marco Legal Estable.
Para que la gestión centralizada del sistema resulte eficiente, es necesario que la
entidad que ha de tomar las decisiones lo haga manejando una información perfecta.
Sin embargo, existen asimetrías de información: el operador del sistema no conoce
todos los datos relevantes, sino que son las empresas las que poseen la mejor
información disponible sobre sus centrales.
Por otro lado, la voluntad del responsable del sistema en la búsqueda de la mayor
eficiencia posible resulta muy importante. En ocasiones, el empeño del organismo
encargado de la explotación es cuestionable. Por ejemplo, si el sector se maneja como
un departamento dentro de un gran ministerio, el interés y esfuerzo que pueden poner
11
2 El mercado eléctrico
esos funcionarios en lograr la mejor planificación y operación es a veces mejorable.
Además, siempre se pueden producir errores en las decisiones tomadas debido a fallos
de apreciación u otros motivos. En algunos países, por ejemplo, se han diseñado
centrales eléctricas de muy gran tamaño en comparación con el total de las necesidades
energéticas del país. Estas centrales resultaban muy atractivas en términos de gran obra
de ingeniería, pero suponían enormes riesgos económicos (y también técnicos) que no
fueron suficientemente tenidos en cuenta. Cuando se producen estos errores en las
decisiones tomadas por una entidad centralizada, son los consumidores los que pagan
los extracostes.
También se dan algunos casos en los que se producen interferencias entre los papeles
del gobierno como regulador y como propietario. Esto puede hacer que se introduzcan
en la regulación del sistema eléctrico criterios ajenos al mismo (protección de las zonas
mineras, objetivos generales de inflación, etc.) que terminan distorsionando
completamente el funcionamiento del sector y conducen a medio plazo a la aparición
de ineficiencias y situaciones absurdas en la operación del sistema.
2.1.2
Mercados con competencia perfecta
Todos los problemas anteriores son motivos para intentar quitar protagonismo en la
operación de los sistemas eléctricos a las autoridades que centralizadamente toman
decisiones sobre el sector e intentar diseñar esquemas que permitan que sean los
distintos agentes generadores y los consumidores los que tomen las decisiones más
importantes.
El proceso de liberalización traslada el riesgo a las empresas privadas, de forma que
éstas dedicarán mayor atención a sus estudios e inversiones ya que lo que está en juego
es su propio dinero. Si se comete un error, éste ya no repercutirá en los consumidores,
sino que sus consecuencias las sufrirá la empresa que lo cometa. Por tanto, con la
desregulación del sector existen más incentivos para maximizar la eficiencia
económica, puesto que el beneficio de las empresas depende directamente de sus
decisiones. Por ejemplo, si una empresa decide la construcción de una central que no
resulta adecuada o eficiente, el mercado penalizará esta decisión. El hecho de que
exista un conjunto de agentes tomando decisiones hace que el mercado escoja a las
empresas más eficientes, por lo que el error de una empresa no tiene por qué afectar a
los consumidores. En un sistema centralizado, los consumidores no tienen posibilidad
de elegir, así que el error del único agente existente les afectará inevitablemente.
Para que la desregulación del sector eléctrico haya sido posible se han tenido que
producir una serie de hechos, que resultaron fundamentales para que se iniciara la
tendencia liberalizadora que existe en muchas partes del mundo.
Uno de los factores más importantes ha sido el aumento del tamaño de los sistemas
eléctricos, que reduce considerablemente los efectos de las economías de escala. El
aumento de la capacidad de transporte de las redes amplía los mercados a los que
pueden acceder las empresas desde sus distintas centrales.
12
2.1 Organización del mercado eléctrico
Por otro lado, el desarrollo de nuevas tecnologías también ha contribuido a hacer que
las economías de escala no sean tan importantes como solían ser. Hoy en día, la
tecnología más interesante parece ser la de las centrales de ciclo combinado, que tienen
eficiencias máximas con tamaños del orden de los 400 MW, muy por debajo de, por
ejemplo, los 1000 MW de una central nuclear. Por tanto, las inversiones no tienen que
ser necesariamente tan elevadas, lo que permite la aparición de empresas más
pequeñas capaces de sobrevivir frente a las grandes compañías. Además, estas
centrales requieren menores tiempos de construcción que las plantas de otras
tecnologías, lo que posibilita que las empresas comiencen a recuperar antes las
inversiones de capital realizadas.
El gran desarrollo tecnológico que se ha producido en los últimos tiempos en las
comunicaciones, las mediciones y el procesado de información ha sido un aspecto
crítico para el sector eléctrico y su liberalización, pues con ello se facilitan los procesos
necesarios para el funcionamiento del mercado y se reducen los costes que éstos
conllevan.
Análisis microeconómico
En un mercado en competencia las empresas toman sus decisiones para maximizar su
propio beneficio, así que en principio no está garantizado que el sistema se comporte
de la forma más eficiente. Este hecho fue objeto de estudio1 del análisis
microeconómico para determinar hasta qué punto es razonable organizar el sector
eléctrico como un mercado competitivo.
Para ello, se propone un ejercicio en el que se compara la operación de un sistema
eléctrico teórico regulado mediante dos esquemas distintos. En el primer modelo, las
decisiones se toman de forma óptima desde el punto de vista centralizado y con
información perfecta, lo que permitiría obtener la mejor solución posible para el
sistema tradicional. En el segundo, cada agente toma sus decisiones maximizando su
propio beneficio en función del precio del mercado y en condiciones de competencia
perfecta. En estas condiciones, el tamaño relativo de cada empresa respecto al tamaño
global del sistema es pequeño, así que las decisiones de producción de las compañías
no pueden modificar significativamente el precio del mercado. Entonces, las empresas
deciden su producción asumiendo que el precio de mercado es independiente de sus
decisiones.
La optimización de la operación de forma centralizada se puede representar de forma
simplificada por el siguiente problema de minimización de costes:
1
Schweppe et al. (1988).
13
2 El mercado eléctrico
min C ( gi )
∑ gi = D
s.a.
⊥ρ
i
gi ≤ g i
⊥ µig
gi ≥ g i
⊥ µi
g
;
∀i
;
∀i
(2.1)
donde
gi
es la producción de energía del equipo i,
gi
gi
es la máxima potencia del grupo i,
D
es la demanda de energía que debe ser satisfecha,
son los costes de operación, que dependen de las cantidades
es el mínimo técnico del grupo i,
C ( gi )
producidas por cada generador,
ρ,
µig
y
g
µi
son las variables duales asociadas a las restricciones del
problema.
Para resolver este problema, se puede construir el lagrangiano asociado al problema:


L = C ( gi ) − ρ ⋅  ∑ gi − D  − ∑ µig ⋅ ( gi − gi ) − ∑ µig ⋅ ( gi − gi )


i
i
(2.2)
i
Para hallar el mínimo coste de operación del sistema se deriva la función lagrangiana
respecto a la generación de cada grupo y se iguala a cero:
∂L ∂C ( gi )
g
=
− ρ − µig + µi = 0
∂gi
∂gi
∀i
(2.3)
El generador marginal j se encontrará funcionando entre sus límites de producción
máximo y mínimo. Por tanto, las variables duales asociadas a las restricciones de
(
g
)
capacidad de este grupo serán nulas µ gj = µ j = 0 .
Para este generador marginal j, la ecuación queda:
( )
∂L ∂C g j
=
−ρ =0
∂g j
∂g j
14
(2.4)
2.1 Organización del mercado eléctrico
De donde:
ρ=
( )
∂C g j
(2.5)
∂g j
Es decir, en la decisión óptima de un sistema centralizado se cumple que el
multiplicador ρ2 es igual al coste marginal del grupo que completa la generación de
energía.
Ahora se estudia el caso de un mercado eléctrico con una estructura de competencia
perfecta. En una situación de competencia perfecta, cada una de las empresas buscará
conseguir el máximo beneficio posible, suponiendo que no pueden modificar
individualmente el precio de la energía, que es percibido como constante por las
empresas generadoras.
El problema que se pretende resolver es el siguiente:
max Be = ∑ p ⋅ gi − C ( gi )
∀e, i ∈ e
i∈e
s.a.
gi ≤ g i
⊥ µig
gi ≥ g i
⊥ µi
g
;
∀i
;
∀i
(2.6)
donde
p es el precio de mercado de la energía eléctrica.
Al igual que se hizo anteriormente, se construye el lagrangiano asociado para resolver
el problema.
Le = ∑ p ⋅ gi − C ( gi ) − ∑ µig ⋅ ( gi − gi ) − ∑ µig ⋅ ( gi − gi )
i∈e
i
(2.7)
i
Para conseguir el máximo beneficio se deriva e iguala a cero esta función. Se obtiene:
∂C ( gi )
∂Le
g
= p−
− µig + µi = 0
∂gi
∂gi
∀i ∈ e
(2.8)
Este multiplicador representa cuánto cambia la función objetivo, es decir, cuánto se
incrementan los costes de producción del sistema, cuando la demanda aumenta 1 MWh; esto es,
el coste marginal del sistema.
2
15
2 El mercado eléctrico
Si se considera el generador marginal del sistema,
( )
∂C g j
∂Le
= p−
=0
∂g j
∂g j
(2.9)
Entonces,
p=
( )
∂C g j
(2.10)
∂g j
A continuación se reúnen los resultados de este caso de mercado en competencia
perfecta y los resultados de un sistema centralizado.
Sistema centralizado
ρ=
ρ=
∂C ( gi )
∂gi
g
− µig + µi
( )
∂C g j
Mercado en competencia perfecta
∀i
p=
p=
∂g j
∂C ( gi )
∂gi
g
− µig + µi
∀i
( )
∂C g j
∂g j
Comparando estas expresiones, se concluye que basta con igualar el precio del
mercado p con el valor del multiplicador ρ del sistema centralizado para que los
resultados de ambos casos sean iguales.
p=ρ=
( )
∂C g j
∂g j
(2.11)
Por tanto, si en unas condiciones de competencia perfecta se establece que el precio de
la energía sea igual al coste marginal del grupo que opera para completar la
producción necesaria, se obtienen los mismos resultados que operando el sistema de
forma centralizada3.
Así, si se dan las condiciones de competencia perfecta, un mercado de electricidad
puede gestionarse con el mismo resultado que un sistema centralizado, pero sin
necesidad de que exista un agente centralizado único que decida cómo debe operarse
El análisis microeconómico incluye también el estudio de las señales óptimas para el equilibrio
de largo plazo. Concluye igualmente que la remuneración de la producción de los agentes al
coste marginal del sistema incentiva la toma de las decisiones de inversión óptimas.
3
16
2.1 Organización del mercado eléctrico
el sistema, con lo que se evitan las ineficiencias derivadas de la toma de decisiones
centralizada. En el nuevo marco serían las empresas las encargadas de decidir,
contando con un gran incentivo que es la optimización de sus propios beneficios.
La conjunción de los hechos comentados anteriormente y los resultados que la teoría
económica ofrece en su aplicación al sector eléctrico es lo que ha motivado el impulso
liberalizador que experimenta este sector desde hace unos años.
2.1.3
Mercados con competencia imperfecta
Aunque lo deseable resulte la competencia perfecta, en la práctica no se dan las
condiciones necesarias para alcanzar esta situación en el sector eléctrico. En el
desarrollo anterior se ha supuesto que ninguna empresa era capaz de influir
significativamente en el precio. Para que esta condición se cumpla es preciso que cada
empresa produzca solamente una cantidad pequeña en relación al volumen total del
mercado. Y para que esto ocurra no solamente se requiere que existan muchas
empresas, sino también que la solución óptima del problema asigne una proporción
pequeña de la producción a cada empresa. La elasticidad de la demanda también juega
un papel muy importante en la capacidad de las empresas para influir en los precios
del mercado: cuanto mayor es la elasticidad de la demanda, menor capacidad tienen
las empresas para influir en el precio; por el contrario, si la demanda es muy inelástica,
como en el caso del sector eléctrico, la dependencia del precio de las decisiones los
agentes se vuelve más importante.
En muchos de los mercados eléctricos no se verifican las condiciones de competencia
perfecta, sino que las actividades eléctricas en un entorno de mercado suelen realizarse
por un número reducido de empresas con un tamaño considerable. En esta situación
existen unos pocos competidores, de forma que alguno o algunos de ellos pueden
influir en el precio. Así que en un mercado oligopolista, las empresas podrían
distorsionar sus decisiones respecto a las de competencia perfecta para conseguir que
el precio de la energía sea más alto y que sus beneficios aumenten, de modo que el
sistema termine siendo más ineficiente.
Por tanto, los resultados del análisis microeconómico no son aplicables a la realidad, ya
que la existencia de un oligopolio introduce distorsiones sobre los resultados del
mercado perfecto y, en consecuencia, sobre los resultados de decisión óptima de un
sistema centralizado. Esto podría considerarse como una razón que justifica la
necesidad de que exista un monopolio regulado. Sin embargo, la regulación tradicional
también presenta ciertos problemas y, en determinadas circunstancias, un mercado
oligopolista resulta preferible al enfoque centralizado.
La regulación tradicional conlleva siempre un cierto nivel de ineficiencia que hace que,
en general, resulte más cara que un mercado perfecto. Si el número de productores en
un mercado no es muy pequeño, los resultados pueden resultar más eficientes que los
del entorno regulado. Los precios de la energía serán menores y esto beneficiará a los
consumidores (ver Figura 2.1). De existir muy pocos productores y de tamaño
considerable, tendrán mucho poder sobre el precio y podrán hacer que éste aumente
17
2 El mercado eléctrico
sensiblemente reduciendo su producción, para así aumentar sus beneficios. Esto
provoca un enorme perjuicio a los consumidores, resulta muy ineficiente y por tanto
altamente indeseable, de modo que en este caso la regulación tradicional sí es
preferible. Así que se establece un cierto umbral a partir del cual, si la competencia es
mayor, aún siendo imperfecta produce mejores resultados que los de la regulación
tradicional. A todos estos estados de competencia imperfecta más eficientes que la
regulación centralizada se les conoce como mercados de competencia practicable.
p
oligopolio
centralizado
nº agentes
Figura 2.1: Competencia practicable
2.2 Mercados spot y mercados a plazo
Los mercados eléctricos spot son mercados al contado en los que las transacciones que
se realizan son de muy corto plazo. En este mercado se determinan las cantidades que
producirá o consumirá por cada uno de los agentes y el precio que deben recibir o
pagar por ello. Las operaciones de compra-venta de energía tienen una fecha de
entrega casi inmediata, normalmente, al cabo de un día o unas pocas horas.
Los mercados a plazo ofrecen la posibilidad a los agentes de negociar parte de su
energía mediante transacciones a plazo. En este caso, la fecha de entrega de la energía
negociada tiene lugar a lo largo de un periodo futuro, de modo que se acuerda la venta
o compra de energía para el siguiente mes, el siguiente trimestre, el siguiente año...
Existen dos tipos básicos de contratos a plazo:
• Los contratos forward, que consisten en un acuerdo de compra o venta de energía
para un cierto periodo futuro a un precio determinado. Los términos de estos
contratos se fijan por las partes que lo negocian en función de las necesidades o
características que deseen. Los contratos forward se negocian en los mercados
OTC (Over The Counter), de naturaleza estrictamente bilateral, que se caracterizan
por estar organizados alrededor de un conjunto de brokers.
• Los contratos de futuro, que son contratos forward en los que la cantidad de
energía y la fecha de entrega están estandarizados. Estos contratos estándar se
18
2.2 Mercados spot y mercados a plazo
negocian en mercados organizados, donde el proceso de negociación está
reglamentado. Existe, además, una cámara de compensación que actúa como
contraparte de los agentes que negocian un contrato, eliminando el riesgo de
contrapartida.
La mayoría de los mercados eléctricos existentes cuentan con mercados a plazo donde
se negocian importantes volúmenes de energía. El caso español constituye una
excepción, ya que hasta la reciente implantación del Mercado Ibérico de la Electricidad
(MIBEL) no ha habido ningún mercado a plazo organizado donde los agentes
españoles pudieran negociar su energía y, aunque la regulación sí permitía la
celebración de contratos bilaterales, éstos han jugado un papel insignificante en la
venta de electricidad. Hay que señalar que la regulación penalizaba hasta el año 2005 a
los generadores participantes en un contrato bilateral, excluyéndolos del pago por
garantía de potencia, de modo que los agentes tenían fuertes incentivos para acudir al
mercado spot. Así, más del 95% de la energía se negociaba en el mercado spot, situación
que contrasta con otros mercados liberalizados del resto del mundo. Por ejemplo, en el
mercado spot del NordPool (Noruega, Finlandia, Suecia y parte de Dinamarca) se
negocia cerca del 45% del total de las transacciones de energía, en el mercado spot de
APX en Holanda se negocia entre un 10% y un 15% de la demanda de energía, y en
Alemania alrededor del 15% de la energía se negocia en el mercado spot EEX. Por tanto,
todo parece indicar que esta situación cambiará pronto en España, impulsada también
por medidas regulatorias que fijan en estos comienzos de los mercados a plazo ciertas
obligaciones de compra a las distribuidoras, que deben adquirir parte de su energía a
plazo.
Los mercados a plazo permiten negociar con anterioridad la energía de un cierto
periodo. Esto ofrece a los agentes que operan en un mercado spot la posibilidad de
gestionar su riesgo de precio asegurándose, por ejemplo, la venta de una determinada
cantidad de energía a un precio fijo para un cierto periodo. Así, los mercados a plazo
pueden emplearse como herramientas de gestión del riesgo, disminuyendo los efectos
de la volatilidad de los precios spot sobre los agentes contratados.
Sin embargo, la existencia de mercados a plazo podría influir en el comportamiento de
los agentes en el mercado spot. Esta tesis de máster se centra en el problema de la
interacción entre los mercados eléctricos a plazo y los mercados eléctricos al contado,
desarrollando diferentes modelos que profundizan en la cuestión de los posibles
efectos de la contratación a plazo sobre el comportamiento estratégico de las empresas
en el mercado spot. En cualquier caso, el estudio se limita a un análisis exclusivamente
teórico del mercado.
19
2 El mercado eléctrico
2.3 Modelos de planificación de la operación en un
mercado en competencia imperfecta
2.3.1
Organización jerárquica de la planificación
La introducción de mecanismos de mercado traslada la responsabilidad de la toma de
decisiones a las empresas generadoras. Al mismo tiempo el riesgo de estas decisiones
pasa a ser asumido por los productores, cuando antes recaía en los consumidores. Por
tanto, la planificación cobra un papel muy importante en las actividades de las
empresas para enfrentarse adecuadamente al entorno liberalizado.
Modelos de largo plazo
Instalación de capacidad de generación
Contratos a largo plazo
Gestión de embalses hiperanuales
Programa de mantenimiento
• Capacidad instalada
• Contratos a largo plazo
Modelos de medio plazo
Explotación de la generación
Gestión estacional de embalses
• Cantidades objetivo
• Curvas de valor de agua
Modelos de corto plazo
Operación de la generación
Programación horaria de la generación
Ofertas a los mercados de energía
Figura 2.2: Organización jerárquica de los modelos de planificación
El objetivo de los estudios de planificación será diferente según el alcance temporal del
estudio, por lo que se divide la planificación de acuerdo a este criterio. Las funciones
de planificación se organizan de forma jerárquica, desde el plazo más largo al más
corto, de modo que los resultados de los modelos de mayor alcance proporcionan
información y consignas para los siguientes, de menor alcance. Con esta desagregación
se puede abordar el estudio de la manera más apropiada para cada horizonte,
utilizando distintos modelos para representar mejor las características más relevantes
de cada estudio. Por ejemplo, para realizar las ofertas al mercado diario es necesario
20
2.3 Modelos de planificación de la operación en un mercado en competencia imperfecta
modelar con bastante rigor el funcionamiento de los equipos, mientras que para decidir
el programa de inversiones esto no resulta operativo.
La estructura jerárquica que presentan las funciones de planificación se representa
esquemáticamente en la Figura 2.2. En ella se refleja cómo los modelos de orden
superior determinan consignas que deben seguir los modelos que se encuentren por
debajo de ellos.
2.3.2
Tipos de modelos de planificación
El nuevo marco regulatorio ha supuesto un gran cambio para los procesos de
planificación que desarrollan las empresas generadoras, dotándolos de mayor
importancia. En los sistemas centralizados, sólo era necesario conocer los costes y
características técnicas de los grupos del sistema para determinar el despacho óptimo.
Sin embargo, en un entorno de competencia las empresas intentan maximizar su
beneficio, que depende del precio del mercado que, a su vez, depende del
comportamiento de cada empresa y, en particular, de las acciones de los competidores.
Es decir, para tomar sus decisiones cada empresa debe estimar el comportamiento del
resto de los agentes. Esto supone una notable dificultad añadida respecto a los modelos
tradicionales. Existen dos grandes líneas de trabajo para llevar a cabo esta estimación:
• Modelos de oferta, que utilizan fundamentalmente datos históricos
• Modelos de equilibrio, que se basan en la teoría de juegos
Modelos del mercado de la energía
Modelos de oferta
Precio
dependiente
de la
producción
Precio
exógeno
Modelos de equilibrio
Equilibrio de
Cournot
Equilibrio en
funciones de
suministro
Figura 2.3: Clasificación de los modelos de programación de generación
Modelos de oferta
En los modelos de oferta, los mecanismos de mercado se introducen por medio del
modelado del precio de la energía, que depende de la producción de la compañía. El
comportamiento de los competidores se intenta predecir a través de series temporales,
estudios de datos históricos y de la estrategia que cada empresa está siguiendo en la
21
2 El mercado eléctrico
actualidad. Con las predicciones sobre la demanda de energía y las de las actuaciones
de la competencia, se crea una función de demanda residual, que relaciona el precio
que el mercado determinará para la energía con la generación de la empresa. La
influencia de la situación de mercado en las decisiones de la empresa es considerada
por medio de esta función de demanda residual.
En modelos más simples el precio se considera como una variable exógena, que no
depende de las decisiones de la empresa. En este caso, se estaría ante un modelo de
competencia perfecta.
En ambos casos se trata de problemas de maximización de los beneficios de las
empresas, donde se incluyen restricciones que han de ser satisfechas por la
programación resultante del modelo.
Se puede introducir la incertidumbre tanto en el comportamiento del precio como en el
de la demanda, creando así modelos probabilistas.
Modelos de equilibrio
Los estudios que calculan el equilibrio del mercado hacen uso de métodos basados en
la teoría de juegos para su resolución. La mayoría de ellos se basan en la búsqueda del
equilibrio en el sentido establecido por Nash. El equilibrio de Nash es el resultado de
un juego en el que ningún jugador puede mejorar su situación modificando de forma
unilateral su estrategia. En este caso, el juego es el mercado eléctrico y la situación de
un jugador o empresa está definida por sus beneficios.
La idea fundamental consiste en que, en lugar de hacer uso de datos históricos sobre el
comportamiento de los competidores, se intentan formular hipótesis razonables sobre
su comportamiento (que de alguna forma intentan expresar el hecho de que los
competidores también quieren maximizar su beneficio) para, de esta forma, inferir
cuáles son las decisiones más razonables que se pueden esperar del resto de las
empresas de la competencia.
De la maximización simultánea de los beneficios de cada empresa se obtiene el
equilibrio del mercado.
El precio de la energía en los mercados eléctricos varía con el tiempo. En general, se
puede suponer que estas fluctuaciones pueden descomponerse en una serie de
oscilaciones alrededor de una tendencia, que está determinada por el equilibrio del
mercado en cada instante. Para estudios de corto plazo, se puede considerar que el
equilibrio del mercado no varía porque no cambian los equipos existentes en el sistema
y, en este caso, lo relevante es captar las oscilaciones alrededor del punto de equilibrio.
Para hacerlo, los modelos que se basan en datos históricos resultan muy apropiados,
porque la información del pasado recoge suficientemente bien esta componente del
precio.
22
2.3 Modelos de planificación de la operación en un mercado en competencia imperfecta
Sin embargo, en el medio y largo plazo el punto de equilibrio varía debido a cambios
en la estructura del sector, como la introducción de nuevas tecnologías o las decisiones
de inversión. Estas transformaciones hacen que los datos históricos no sean
suficientemente representativos de la nueva situación. Entonces, en estos casos es más
interesante capturar el valor medio del precio que el ruido alrededor de éste. Por este
motivo, los modelos de equilibrio son más adecuados cuando se quiere observar la
evolución del sistema a largo plazo.
2.3.3
Modelos clásicos de equilibrio
Esta tesis de máster se centra en los modelos de equilibrio. A continuación se revisan
distintos planteamientos fundamentales para el cálculo del equilibrio del mercado,
poniendo especial interés en el modelo de Cournot por su importancia y extensión.
Modelo de Cournot
Dentro de los modelos que pretenden la representación del equilibrio del mercado, el
modelo de Cournot es el que ha sido utilizado como base en la mayoría de los estudios.
El modelo de Cournot representa un juego donde todos los competidores toman su
decisión simultáneamente. Su principal característica es que se compite en cantidades,
esto es, la decisión que toma cada empresa es la cantidad que ofrece al mercado.
El modelo de Cournot consiste en resolver simultáneamente todos los problemas de
maximización del beneficio de todas las empresas. El beneficio de una empresa e viene
dado por:
Be = p ⋅ qe − Ce ( qe )
donde
(2.12)
es el precio del mercado,
es la producción de una empresa e,
p
qe
∀e
Ce ( qe )
son los costes de cada empresa e, que dependen de la cantidad
producida.
Los consumidores se representan mediante la curva de demanda agregada, necesaria
para establecer el precio. Esta curva expresa el precio en función de la cantidad total
producida por el sistema, de forma que, fijadas las producciones de las empresas, el
precio se convierte en una variable dependiente que se obtiene de la curva de la
demanda.


p = f  ∑ qe 
 e

(2.13)
Se busca la cantidad que maximiza el beneficio de cada empresa, para lo que se deriva
este beneficio respecto a su producción y se iguala a cero, obteniendo la siguiente
condición de optimalidad para cada empresa:
23
2 El mercado eléctrico
∂Be
∂p ∂C ( qe )
= p + qe ⋅
−
=0
∂qe
∂qe
∂qe
El problema es determinar cuánto vale
∀e
(2.14)
∂p
. La dificultad reside en el hecho de que en
∂qe
el caso oligopolista es preciso conocer la reacción de las demás empresas, es decir,
cómo varían las producciones de las empresas competidoras cuando la empresa e
 ∂qee

, ee ≠ e  . Llamando Q a la cantidad total producida en
 ∂qe

modifica su generación 
el sistema,
Q = qe +
∑ qee
(2.15)
ee ≠e
la derivada del precio respecto a la producción de la empresa e está dada por:
∂p ∂p ∂Q
=
⋅
∂qe ∂Q ∂qe
∀e
(2.16)
Para resolver el problema se introduce la conjetura de Cournot, que supone que la
reacción de los competidores es no hacer nada. Esta hipótesis considera un caso
particular del equilibrio de Nash en el que la cantidad ofertada por cada empresa es
independiente de las cantidades de las otras empresas. Es decir, la curva de oferta de
una empresa es totalmente vertical y, en consecuencia, la derivada de las cantidades de
 ∂qee

= 0 , ee ≠ e  . Introduciendo esta
 ∂qe

las demás empresas respecto a la suya es nula 
hipótesis en la ecuación (2.16),
∂Q
=1
∂qe
⇒
∂p ∂p ∂Q ∂p
=
⋅
=
∂qe ∂Q ∂qe ∂Q
∀e
(2.17)
La derivada del beneficio de una empresa respecto a su producción queda:
∂Be
∂p ∂C ( qe )
= p + qe ⋅
−
=0
∂qe
∂Q
∂qe
En esta ecuación,
∀e
(2.18)
∂C ( qe )
∂p
es la pendiente de la curva de demanda y
son los costes
∂qe
∂Q
marginales de la empresa en el punto de producción. De cada ecuación de optimalidad
se deduce que, en el punto de equilibrio, los ingresos marginales son iguales a los
costes marginales para cada empresa:
p + qe ⋅
24
∂p ∂C ( qe )
=
∂Q
∂qe
∀e
(2.19)
2.3 Modelos de planificación de la operación en un mercado en competencia imperfecta
La resolución de este sistema de E ecuaciones determina el equilibrio de Cournot.
El modelo de Cournot se adapta bien a la representación de sistemas térmicos,
ofreciendo resultados acordes con los que la realidad determina. Tiene el respaldo
teórico del equilibrio de Nash y empíricamente ha demostrado la bondad de sus
resultados, de ahí que se mantenga en plena vigencia en los estudios de planificación.
Modelo de Bertrand
Si en el modelo de Cournot la competencia es en cantidades, en el de Bertrand se
compite con el precio. Cada empresa ofrece toda su producción a un precio
determinado y, por tanto, la curva de oferta es completamente horizontal. Todas las
ofertas se realizan simultáneamente para cubrir una demanda que se considera
constante e independiente del precio. De esta forma, las ofertas de menor precio son las
seleccionadas para atender la demanda.
Los resultados que ofrece este modelo no se corresponden con los que se obtienen en la
realidad en los mercados eléctricos. Uno de sus grandes inconvenientes es que no tiene
en cuenta las limitaciones de capacidad de generación que tienen las empresas. Por
tanto, este modelo no refleja satisfactoriamente los mercados de la energía eléctrica.
Modelo de equilibrio en funciones de suministro (SFE)
La competencia en este modelo no se produce sólo por precio o sólo por cantidad, sino
que se hace con una combinación de ambas. La estrategia de una empresa se define con
una función que relaciona precio y cantidad producida, la función de suministro de la
empresa. Ésta es la curva de oferta de la empresa. El propio modelo es el que
determina la forma de esta función de suministro. Es un modelo más realista en cuanto
a la representación de la forma de competencia.
Sin embargo, este planteamiento da lugar a un sistema de ecuaciones diferenciales que
resulta muy difícil de tratar. Cuando las empresas generadoras se enfrentan a cierta
incertidumbre en el comportamiento de la demanda, este enfoque resulta
especialmente apropiado. Cuando no hay incertidumbre, la solución está
indeterminada y el equilibrio en funciones de oferta no es aconsejable.
Modelo de equilibrio en variaciones conjeturales
En este caso, también se considera que tanto el precio como la cantidad son variables
pero, a diferencia del equilibrio en funciones de suministro, están relacionados
linealmente, por lo que las curvas de oferta son rectas.
Este modelo presenta la ventaja frente al SFE de que tiene un único grado de libertad,
por lo que puede resolverse sin indeterminación sin necesidad de introducir
incertidumbre en la demanda (como en el modelo de Cournot). Frente al modelo de
Cournot, tiene la ventaja de que no depende de la elasticidad de la demanda, por lo
que permite mayor realismo en la determinación de los precios.
25
2 El mercado eléctrico
Modelo de Stackelberg
En este modelo se compite en cantidades pero, a diferencia del modelo de Cournot, las
ofertas no se realizan simultáneamente. El proceso de oferta se produce en dos fases:
una empresa decide su producción y, posteriormente, el resto de las empresas
(denominadas seguidoras) seleccionan la cantidad óptima que deben producir en
función de la decisión de la empresa líder. Para resolverlo se analiza primero la
segunda fase y luego se vuelve hacia atrás. La empresa líder obtiene ventajas por
adelantar su decisión y consigue unos beneficios superiores a los que tendría en el
equilibrio de Cournot.
Los mercados eléctricos reciben las ofertas de forma simultánea, por lo que este tipo de
modelo en dos fases no resulta muy adecuado. Se adapta mejor al problema de
decisión de la ampliación de la capacidad de generación donde, si una empresa se
adelanta, el resto de las empresas actuarán ya condicionadas por su decisión.
Modelo de liderazgo en la elección del precio
El modelo de liderazgo en la elección del precio es similar al de Stackelberg pero con
competencia en precio. También se estudia en primer lugar la segunda fase y después
la primera. En este caso son las empresas seguidoras las que obtienen mejores
resultados al aprovechar que conocen la actuación de la empresa líder.
No es aplicable a los mercados eléctricos por los mismos motivos que el modelo de
Bertrand, es decir, no refleja adecuadamente las restricciones de capacidad, que son un
elemento fundamental en un mercado eléctrico.
2.4
Modelos del comportamiento estratégico en los
mercados a plazo
La mayoría de los modelos que se han desarrollado hasta ahora para calcular el
equilibrio de los mercados eléctricos son modelos de una etapa, que pueden incorporar
más o menos detalles sobre las restricciones técnicas de los equipos (restricciones
hidráulicas,...). Estos modelos permiten obtener resultados satisfactorios para el
problema de la producción de los agentes en un mercado spot.
El modelado de equilibrio de los mercados eléctricos incorporando la existencia de
mercados a plazo está mucho menos desarrollado. Uno de los trabajos más relevantes
sobre el problema de la interacción entre los mercados a plazo y los mercados spot es
Allaz y Vila (1993). Este modelo describe un equilibrio no colusivo en dos etapas y
concluye que los contratos a plazo tienen un efecto procompetitivo, ya que reducen la
cantidad de energía que puede beneficiarse de un incremento del precio spot. Según
Allaz y Vila, la existencia de mercados a plazo influye en el comportamiento de los
agentes que operan en el mercado spot de manera tal que las empresas aumentan su
producción respecto al equilibrio de un único mercado de corto plazo, reduciendo con
26
2.4 Modelos del comportamiento estratégico en los mercados a plazo
ello el precio de la energía y acercándose a los resultados de competencia perfecta.
Allaz y Vila muestran que contratar en un mercado a plazo supone una ventaja
competitiva respecto a no negociar contratos, luego las empresas tienen incentivos
estratégicos para participar en estos mercados.
Esta capacidad de los contratos a plazo para reducir los incentivos de los agentes para
ejercer su poder de mercado en el spot ha sido ampliamente estudiado –véase, por
ejemplo, Von der Fer y Harbord (1993), Newbery (1998), Green (1999) o Wolak (2000)–.
Estos resultados se han obtenido bajo diferentes hipótesis del comportamiento de las
empresas en el mercado, que incluyen desde equilibrios de Cournot hasta equilibrios
en funciones de suministro.
Sin embargo, Mahenc y Salanié (2004) identifica algunos casos en los que la existencia
de mercados a plazo puede incrementar el poder de mercado de los agentes. El modelo
considera un juego repetido en el que dos duopolistas compiten en un mercado spot
según el modelo de Bertrand. Los resultados del modelo muestran que, en el equilibrio,
las empresas pueden comprar parte de su propia energía a plazo, lo que eleva los
precios respecto al caso en el que no existen mercados a plazo.
En los últimos años se han desarrollado diversos trabajos que consideran la naturaleza
repetida de la interacción entre mercados a plazo y spot y concluyen que, en este caso,
aparecen diferentes efectos que compensan el efecto procompetitivo del modelo de
Allaz y Vila. Existen dos líneas fundamentales de trabajo: un primer enfoque que se
centra en la posible aparición de estrategias cooperativa entre los agentes, y una
segunda línea que investiga el problema en el marco de un juego dinámico no colusivo.
Dentro del primer grupo, Ferreira (2001) estudia un modelo idéntico al de Allaz y Vila
(y, por tanto, no repetido) salvo porque el número de periodos anteriores al mercado
spot en los que las empresas pueden negociar su energía a plazo es infinito. Los
resultados parecen estar en la línea de un folk theorem: cualquier resultado entre el
equilibrio competitivo y el equilibrio de Cournot es posible. A continuación, el artículo
analiza los diferentes equilibrios cuando se considera la existencia de mercados a plazo
posteriores al spot donde renegociar los contratos adquiridos, y muestra que la solución
del equilibrio de Cournot puede mantenerse en este caso, mientras que la solución
competitiva no es sostenible.
Le Coq (2004) describe un modelo en el que dos empresas firman contratos de largo
plazo con comercializadores para el suministro de su energía y, posteriormente,
interactúan repetidamente en el mercado spot. Le Coq muestra que los mercados a
plazo contribuyen a mantener una colusión en el mercado spot. De hecho, los contratos
hacen posible la aparición de estrategias cooperativas entre los agentes que no
existirían si no hubiese mercados a plazo, ya que los incentivos de las empresas para
desviarse de la estrategia colusiva son menores que en un mercado sin contratos.
Liski y Montero (2006) analizan el problema de las empresas que interactúan tanto en
el mercado a plazo como en el mercado spot durante un número infinito de periodos.
En este caso, los generadores que venden energía en el spot pueden, al mismo tiempo,
tomar posiciones compradoras en el mercado a plazo y mantener una colusión tácita.
27
2 El mercado eléctrico
Por tanto, la existencia de mercados a plazo permite a las empresas alcanzar equilibrios
colusivos que de otra forma no serían posibles, de modo que amplían el número de
casos en los que puede sostener una cooperación entre los agentes. Aparece, entonces,
un efecto procolusivo que tiende a dominar, salvo en el caso de que se articulen
medidas regulatorias específicas, compensar en el efecto procompetitivo del modelo
de Allaz y Vila.
En Green y Le Coq (2007) se estudia el efecto de la duración de los contratos a plazo
sobre las posibilidades de mantener una colusión en un juego repetido en el que las
empresas compiten en precios. Los contratos a plazo pueden favorecer la aparición de
estrategias cooperativas, ya que reducen la producción de cada empresa que puede
beneficiarse de una desviación de la estrategia colusiva. Los agentes siempre pueden
mantener un cierto grado de colusión pero, a medida que la duración de los contratos
aumenta, resulta más complicado sostener la cooperación.
Dentro del segundo grupo de trabajos que estudian el comportamiento estratégico de
los agentes en un juego multiperiodo destacan Amaya et al. (2006) y Zhang y
Zwart (2006). En Amaya et al. (2006) se muestra que la existencia de mercados
posteriores al mercado spot puede compensar el efecto procompetitivo de los contratos
a plazo. Zhang y Zwart (2006) plantean un juego repetido en el que un monopolista
propietario de los activos de generación debe vender parte de su energía mediante
contratos a plazo para limitar su poder de mercado. En este contexto, la estrategia del
monopolista tiende a fijar precios elevados, superiores a los que maximizan su
beneficio en cada mercado spot considerado de manera individual, para ganarse una
reputación frente a los compradores del mercado a plazo y mantener, de esta forma, un
precio elevado para sus contratos. Así, los compradores están dispuestos a pagar
mayores precios por los contratos futuros, en la medida en la que esperan que los
precios de la energía en los siguientes periodos sean altos. Tras la negociación de cada
contrato, al monopolista podría interesarle fijar precios más bajos, en línea con los
resultados de Allaz y Vila, pero al hacerlo estaría reduciendo el precio de los contratos
en el siguiente periodo, obteniendo unos beneficios globales menores.
Esta tesis de máster forma parte del esfuerzo por desarrollar nuevos modelos que
puedan recoger el problema de la interacción entre los mercados a plazo y los
mercados spot en toda su complejidad. En concreto, partiendo del modelo de Allaz y
Vila, se pretende corregir algunas deficiencias detectadas y profundizar en el análisis
teórico del comportamiento de los agentes teniendo en cuenta la existencia de los
mercados a plazo.
28
3
Modelo de una etapa
La mayoría de los mercados eléctricos existentes están formados por unas pocas
empresas de tamaño considerable que podrían tener una cierta capacidad para influir
en el precio de la energía a través de sus decisiones de producción. Por tanto, los
modelos tradicionales de minimización de costes ya no representan adecuadamente el
comportamiento de los agentes, y es necesario desarrollar nuevos modelos basados en
teoría de juegos para estudiar el funcionamiento de los mercados en competencia
imperfecta.
En este capítulo se introduce la notación que se empleará en el desarrollo de los
distintos modelos incluidos en la tesis de máster y se presenta una metodología basada
en el problema de complementariedad. Para ilustrar esta forma de plantear y resolver
problemas de equilibrio, se aplica la metodología descrita a un modelo de Cournot de
una etapa adaptado a un entorno de competencia (Ventosa (2001)).
29
3 Modelo de una etapa
3.1 Metodología basada en el problema de
complementariedad
3.1.1
Planteamiento
Una de las cuestiones que se tratan en esta tesis de máster es la búsqueda de un
modelo que represente adecuadamente un mercado oligopolista. El método utilizado
se basa en la formulación matemática del equilibrio del mercado mediante la
consideración de los problemas de optimización que modelan el comportamiento
óptimo de las empresas. De este modo, el comportamiento de cada empresa se
representa mediante su objetivo natural de maximizar el propio beneficio, unido a una
serie de restricciones técnicas que modelan la explotación de forma realista. Este
problema se representa de forma esquemática en la Figura 3.1.
Problema de
optimización de la
empresa 1
maximizar fo1 ( x1 )
sujeto a
h1, j =0
g1, k ≤ 0
Problema de
optimización de la
empresa e
●●●
maximizar foe ( xe )
sujeto a
he , j =0
Problema de
optimización de la
empresa E
●●●
maximizar foE ( xE )
sujeto a
g e, k ≤ 0
hE , j =0
g E ,k ≤ 0
precio − m ( x ) = 0
Mercado de electricidad
Figura 3.1: Formulación matemática del equilibrio del mercado
En la figura se aprecia cómo los problemas de optimización de las empresas que
compiten en el mercado eléctrico están acoplados por la ecuación del precio de
mercado, que es función de la producción total. Este acoplamiento entre problemas es
producto de la interdependencia que tienen las decisiones de las empresas que
compiten por satisfacer la misma demanda. La existencia de un nexo de unión a través
del mercado impide resolver los E problemas de optimización de forma independiente
mediante métodos tradicionales, y hace necesario buscar una forma de resolución
simultánea.
El método propuesto consiste en formular las condiciones de optimalidad de
Karush-Kuhn-Tucker (KKT) de cada problema de optimización para formar un
problema mixto de complementariedad con todas las condiciones de optimalidad que
puede ser resuelto directamente empleando algoritmos específicos.
30
3.1 Metodología basada en el problema de complementariedad
3.1.2
Descripción
El método utilizado para formular el equilibrio del mercado como un problema de
complementariedad se puede dividir en cuatro pasos:
Formulación del problema de optimización de cada empresa
El siguiente cuadro recoge la fracción de la Figura 3.1 correspondiente a la formulación
genérica del problema de optimización de la empresa e.
maximizar
foe ( xe )
sujeto a
he, j = 0
⊥ λe, j
g e,k ≤ 0
⊥ µe, k
Figura 3.2: Problema de optimización de una empresa
donde
he, j y ge,k
representa la función objetivo,
son las variables de decisión de cada empresa,
son las restricciones de igualdad y de desigualdad,
λe, j y µe,k
representan sus variables duales asociadas, respectivamente.
fo
x
Se observa que el problema de optimización de cada empresa es totalmente flexible.
Por un lado, la función objetivo no tiene que ceñirse a la maximización pura del
beneficio obtenido en el mercado, sino que se pueden incluir otros ingresos u objetivos
estratégicos de las empresas. Por otro lado, las restricciones pueden representar todas
las limitaciones técnicas de la generación y todas las limitaciones de carácter estratégico
relacionadas con el mercado que se consideren relevantes, siempre éstas que se puedan
representar mediante funciones convexas. Si el modelado de las restricciones incluye
variables binarias, las condiciones KKT ya no garantizan la optimalidad de la solución.
Las variables duales tienen un claro sentido económico, ya que la variable dual
asociada a una cierta restricción es el beneficio o incremento de la función objetivo que
se obtendría si se relajase unitariamente dicha restricción.
Construcción del lagrangiano del problema de optimización de cada empresa
La construcción del lagrangiano de cada problema de optimización a partir de la
formulación anterior se emplea como una función auxiliar que facilita la obtención de
las condiciones de optimalidad.
Le ( x, λ , µ ) = foe − ∑ λe, j ⋅ he, j − ∑ µe,k ⋅ ge,k
j
(3.1)
k
31
3 Modelo de una etapa
Obsérvese que se ha optado por formular el problema de maximización equivalente,
de forma que las variables duales de las restricciones de desigualdad µe,k resultan
positivas.
Obtención de las condiciones de optimalidad de cada empresa
Las condiciones de optimalidad de cada uno de los problemas de optimización están
formadas por tres conjuntos de ecuaciones:
i. Derivada del lagrangiano respecto de las variables de decisión igual a cero
∂Le
∂xe
=0
(3.2)
Las derivadas del lagrangiano respecto de las variables estratégicas son las que
permiten a cada empresa tomar las decisiones óptimas para maximizar su
función objetivo.
ii. Derivada del lagrangiano respecto de los multiplicadores de las restricciones de
igualdad
∂Le
= he, j = 0
∂λe, j
(3.3)
Las derivadas del lagrangiano respecto de los multiplicadores de las
restricciones de igualdad son las propias restricciones de igualdad. Por tanto,
la función de estas ecuaciones es forzar la factibilidad de la solución.
iii. Condición de complementariedad de holguras
 µe , k ⋅ g e , k = 0

 g e,k ≤ 0

 µe , k ≥ 0
(3.4)
El conjunto de ecuaciones µe,k ⋅ g e,k = 0 impone la relación lógica existente
entre cada restricción de desigualdad g e,k y su variable dual µe,k asociada. Si
la restricción no está activa
( ge,k ≤ 0 ) , la solución óptima del problema ya
cumple esta restricción sin necesidad de forzar que alguna de las variables
tome un determinado valor; por tanto, relajar dicha restricción no tiene ningún
efecto sobre la función objetivo, por lo que su variable dual asociada es igual a
(
)
(
)
cero µe,k = 0 . Si la restricción está activa g e,k = 0 , alguna de las variables
ha modificado su valor óptimo para que el problema sea factible, de modo que
(
)
su variable dual asociada toma un valor distinto cero µe,k ≥ 0 indicando el
32
3.2 Planteamiento del modelo
beneficio adicional que se obtendría si se relajase unitariamente esta
restricción.
Estas ecuaciones no lineales son las que presentan la estructura de un
problema de complementariedad.
Las condiciones de optimalidad forman un sistema de ecuaciones no lineales con la
estructura de un problema mixto de complementariedad (MCP), ya que éste se define
como la unión de un sistema de ecuaciones -derivada del lagrangiano respecto de las
variables de decisión y derivada respecto de los multiplicadores iguales a cero- con un
problema de complementariedad -condición de complementariedad de holguras-.
Formulación del equilibrio del mercado como un problema mixto de
complementariedad
Finalmente, el equilibrio del mercado se formula uniendo las condiciones de
optimalidad de cada empresa e en un único problema mixto de complementariedad,
como se muestra en la Figura 3.3.
En la figura no se ha incluido la ecuación del precio del mercado a través de la que
interactúan los problemas de optimización de los agentes, ya que este vínculo está
considerado dentro de las condiciones de optimalidad de las empresas.
Condiciones de
optimalidad de la
empresa 1
∂L1
∂x1
∂L1
∂λ1, j
=0
∂Le
∀x1
= h1, j = 0
µ1,k ⋅ g 1,k

 g 1,k ≤ 0
µ1,k ≥ 0
Condiciones de
optimalidad de la
empresa e
∀λ1, j
=0
∀µ1, k
∂xe
●●●
∂Le
∂λe , j
=0
∂L E
∀xe
= he , j = 0
µ e , k ⋅ g e , k

 g e,k ≤ 0
µ e,k ≥ 0
Condiciones de
optimalidad de la
empresa E
∀λe , j
=0
∀µ e , k
∂xE
●●●
∂L E
∂λE , j
=0
∀x E
= he , j = 0
µ E , k ⋅ g E , k

 g E ,k ≤ 0
µ E ,k ≥ 0
∀λ E , j
=0
∀µ E , k
Figura 3.3: Formulación matemática del equilibrio del mercado como un problema
mixto de complementariedad
3.2 Planteamiento del modelo
Las empresas que compiten en un mercado eléctrico se enfrentan al problema de
decidir cuál es la cantidad óptima que deben vender al mercado para conseguir los
mayores beneficios posibles. Si la estructura del mercado es oligopolista, los agentes
33
3 Modelo de una etapa
deben tener en cuenta su capacidad para modificar el precio a la hora de tomar sus
decisiones, sabiendo que su ingreso unitario depende, en parte, de la cantidad de
energía que decidan producir. En este capítulo se describe un modelo que representa el
comportamiento de las empresas en un mercado en competencia imperfecta. En este
caso, se considera un estudio de alcance anual agrupado en un único periodo.
El objetivo del problema es el cálculo del equilibrio del mercado, definido como el
punto en el que ninguna empresa puede mejorar sus beneficios modificando de forma
unilateral sus decisiones. Para ello hay que considerar simultáneamente los problemas
de optimización de todas las empresas, lo que hace necesario encontrar una alternativa
a los métodos de resolución tradicionales. En esta tesis de máster se propone la
metodología descrita en 3.1.
El modelo supone que cada empresa tiene uno o varios generadores de su propiedad
con los que produce la cantidad total que vende en el mercado. Los costes de
producción más relevantes en los que incurre un generador térmico para producir
energía son los costes de combustible. No resulta sencillo modelar con precisión cómo
evoluciona el consumo de combustible de un grupo generador cuando cambia la
cantidad de energía producida, ya que depende de múltiples factores. Frecuentemente,
se emplea la representación de la Figura 3.4.
C
c
cb
g
g
g
Figura 3.4: Coste de combustible de un generador térmico
La ordenada en el origen de la recta de la figura anterior, cb, son los costes de
acoplamiento del grupo, es decir, los costes en los que incurre el generador por estar
acoplado a la red. La pendiente de la recta, c, representa el incremento en el coste de
producción cuando aumenta unitariamente la producción del generador, esto es, los
costes variables del grupo. Como se aprecia en la figura, el coste de producción del
grupo se define únicamente para el rango de generación en el que es capaz de
mantener un funcionamiento estable; por tanto, estará definido entre su mínimo
técnico g y su potencia máxima g . Además, existen otros costes asociados a los
procesos de arranque y parada del grupo.
Como es habitual en los modelos de medio y largo plazo, en este modelo los
generadores térmicos se representan por sus costes variables de producción, ya que el
horizonte temporal considerado es suficientemente amplio como para que los costes de
34
3.3 Formulación del problema del equilibrio del mercado
acoplamiento, arranque y parada sean relativamente pequeños frente a los costes
variables. Entonces, es necesario suponer que el mínimo técnico de los grupos de
generación es igual a cero para permitir que existan centrales no acopladas que no
producen energía.
En contraste con la generación térmica, el coste variable de producción de los grupos
de generación hidráulica es prácticamente nulo, aunque en este caso la cantidad de
agua disponible está limitada. Los grupos hidráulicos se modelan agregados por
cuenca, caracterizándolos mediante su potencia máxima y la energía disponible, que
está limitada por la capacidad del embalse.
3.3 Formulación del problema del equilibrio del
mercado
3.3.1
Formulación del problema de optimización de cada
empresa
En un contexto de mercado ya no se realiza una minimización de costes centralizada,
sino que cada empresa tiene como objetivo la maximización de sus beneficios, para lo
que realiza su propia programación de la producción. Además, se deben satisfacer una
serie de restricciones en la operación del sistema.
Función objetivo
foe = p ⋅ qe − Ce
donde
∀e
(3.5)
es el precio de mercado de la energía,
qe es la producción total de la empresa e,
Ce son los costes de producción de la cantidad qe .
p
El objetivo de cada empresa es la maximización de su beneficio, obtenido como los
ingresos procedentes del mercado menos los costes incurridos al generar la producción
vendida.
El primer sumando de la función objetivo representa los ingresos que obtiene cada
empresa de la venta de su producción de energía al mercado eléctrico como el
producto del precio p resultado del mercado por la cantidad total qe producida por la
empresa e. En el segundo sumando aparecen los costes de generación la empresa e.
Puesto que cada empresa posee uno a varios generadores con los que produce su
energía, los costes de producción de la cantidad qe corresponden con los costes de
operación de los equipos de la empresa, dados como el producto del coste unitario de
producción ci del generador i por la producción gi de dicho grupo, para todos los
generadores de la empresa.
35
3 Modelo de una etapa
La función objetivo queda, entonces:
foe = p ⋅ qe − ∑ ci ⋅ gi
∀e
(3.6)
i∈e
siendo
ci el coste variable del generador i,
gi la producción del generador i.
Restricciones y ecuaciones
• Limitación de potencia máxima de los generadores
gi ≤ g i
⊥ µig
; ∀e, i ∈ e
(3.7)
La generación que puede producir un grupo tiene un máximo dado por gi que
depende de su tecnología y su tamaño.
• Limitación de potencia mínima de los generadores
gi ≥ g i
g
⊥ µi
; ∀e, i ∈ e
(3.8)
Para conseguir un funcionamiento estable del grupo se debe alcanzar una
potencia mínima gi conocida como mínimo técnico. Sin embargo, en esta tesis de
máster se tratan modelos de medio plazo en los que se considera que el efecto de
los acoplamientos, arranques y paradas de los grupos es despreciable. Por tanto,
se establece que este valor mínimo sea nulo para permitir que existan grupos no
acoplados.
• Gestión de las reservas hidráulicas
gi ≤ H i
⊥ µiH ; ∀e, i ∈ ( e, ih )
(3.9)
El nivel de reservas hidráulicas se modela de forma simplificada suponiendo
conocida la energía disponible de cada grupo hidráulico para todo el horizonte
considerado. Por tanto, la gestión de las reservas se limita a imponer que la
energía consumida a lo largo de todos los periodos sea menor que la energía total
disponible.
• Producción total de cada empresa
qe = ∑ gi
∀e
(3.10)
i∈e
La producción total de cada empresa e se obtiene como la suma de la generación
de todos sus grupos. Esta ecuación se ha considerado explícitamente con el objeto
de simplificar la notación.
36
3.3 Formulación del problema del equilibrio del mercado
Formulación completa del modelo de optimización
A continuación se recopila el modelo del problema de optimización de cada empresa
para tener una visión global.
max p ⋅ qe − ∑ ci ⋅ gi
∀e
i∈e
s.a.
gi ≤ g i
⊥ µig ;
gi ≥ g i
⊥ µi
gi ≤ H i
⊥ µiH ;
g
;
∀e, i ∈ e
∀e, i ∈ e
∀e, i ∈ ( e, ih )
(3.11)
3.3.2
Construcción del lagrangiano del problema de
optimización de cada empresa
Para la formación del lagrangiano del problema de optimización de cada empresa se ha
seguido el siguiente convenio:
• El problema de optimización es de maximización.
• Todas las restricciones de desigualdad se formulan como inecuaciones de signo
menor o igual, con lo que sus variables duales asociadas son positivas.
Le = p ⋅ qe − ∑ ci ⋅ gi −
i∈e
−∑
i∈e
µig
⋅ ( gi − gi ) −
(
)
− ∑ µi ⋅ gi − gi −
g
i∈e
−
∑
i∈( e,ih )
µiH ⋅ ( gi − H i )
(3.12)
3.3.3
Obtención de las condiciones de optimalidad de cada
empresa
Como se describió en el apartado 3.1.2, las condiciones de optimalidad están formadas
por tres conjuntos de ecuaciones. Sin embargo, en este caso no se han considerado
restricciones de igualdad.
37
3 Modelo de una etapa
Derivada del lagrangiano respecto de las variables de decisión igual a cero
El problema del equilibrio del mercado se resolverá a través del modelo de equilibrio
de Cournot, por lo que la única variable sobre la que pueden decidir las empresas es la
cantidad total de energía que van a producir o, lo que es lo mismo, las potencias
generadas por los grupos de su propiedad.
∂Le ∂p
=
⋅ qe + p − ci −
∂gi ∂gi
g
− µig + µi
∀e, i ∈ e
(3.13)
− µiH = 0
Considérese primero un generador térmico. En este caso, la variable dual asociado a la
(
)
restricción de reservas hidráulicas será igual a cero µi = 0 , ya que esta restricción
H
sólo está definida para los grupos hidráulicos. Si el grupo no está generando en
ninguno de sus límites técnicos, entonces las restricciones de potencia mínima y
potencia máxima no están activas. Las variables duales asociadas a estas restricciones
(
)
g
son nulas µi = µig = 0 , porque la empresa no obtiene ningún beneficio adicional por
poder producir 1 MWh más o menos con ese generador. La ecuación de optimalidad
anterior queda:
p+
donde
∂p
⋅ qe = ci
∂gi
IM i = p +
CM i = ci
∂p
⋅ qe
∂gi
(3.14)
es el ingreso marginal del grupo i,
es el coste marginal del grupo i.
Luego, la producción de un generador marginal que maximiza el beneficio de la
empresa e es aquella que hace que el coste marginal del grupo se iguale a su ingreso
marginal. Dado que el grupo no está produciendo en ninguno de sus límites de
funcionamiento, este generador puede responder ante cambios unitarios en la
demanda, siempre que los ingresos que obtenga por la variación de su producción
igualen el coste de generación incurrido.
Si las empresas compitieran en un mercado en competencia perfecta, ningún agente
tendría poder para influir en el precio de la energía, por lo que el precio de mercado
sería percibido como constante por las empresas generadoras:
∂p
=0
∂gi
∀i
(3.15)
Entonces, la ecuación de optimalidad de un generador marginal sería:
p = ci
38
(3.16)
3.3 Formulación del problema del equilibrio del mercado
Comparando las ecuaciones (3.14) y (3.16), se observa que en un mercado en
competencia imperfecta el ingreso marginal de un generador tiene un término
adicional igual a
∂p
⋅ qe . Este término recoge el efecto que tiene sobre los ingresos del
∂gi
grupo la variación que sufrirá el precio al modificar unitariamente la producción del
generador i. En efecto, se ha comentado que las empresas oligopolistas deben tener en
cuenta cómo sus decisiones afectan al precio de mercado. Por tanto, cuando una
empresa está decidiendo si debe producir 1 MWh adicional, debe comparar dos
términos:
p
∆p
Coste de producción
Precio de la energía
∆qe
q
Figura 3.5: Efectos del incremento de producción sobre el beneficio de una empresa
• El beneficio que obtiene de la venta de ese megavatio-hora adicional, igual a la
diferencia entre el precio que recibe esa unidad de energía y el coste que supone
producirla ( p − ci ) . El área verde de la Figura 3.5 representa este ingreso.
• La reducción de ingresos asociada a la bajada de precio, dada por el término
∂p
⋅ qe . El incremento de generación hace que el precio baje, de modo que toda
∂gi
la producción de la empresa se remunera a un precio menor. Este término,
representado por el área roja de la Figura 3.5, será mayor cuanto mayor sea la
potencia de la empresa que ya está produciendo, conocida como potencia
inframarginal. Si la producción afectada por una bajada de precio tiene un
volumen importante, la empresa tendrá fuertes incentivos para retirar parte de
su generación y mantener los precios altos, consiguiendo así que toda esa
producción capture un precio más elevado. Para empresas pequeñas, es casi
siempre despreciable. Por otro lado, cuanto mayor sea (en valor absoluto) la
derivada del precio respecto a la producción de un grupo, mayor capacidad
tendrá la empresa para modificar el precio y más importante será este término.
Las empresas que compiten en un mercado en competencia imperfecta deben
considerar el efecto global de un aumento de generación sobre sus beneficios, teniendo
en cuenta tanto los ingresos adicionales asociados a la venta de energía, como el
impacto que la correspondiente bajada de precio tiene sobre la remuneración del resto
39
3 Modelo de una etapa
de su producción. De modo que en el proceso de toma de decisiones las empresas
tienen en cuenta la posibilidad de actuar sobre el precio reduciendo la cantidad
generada.
Considérese ahora un generador térmico con alguna restricción activa. En este caso, la
variable dual asociada a la restricción activa supone un coste que hace que la
producción del grupo se modifique para satisfacer la restricción. Por ejemplo, un
generador con coste menor que su ingreso marginal estará produciendo su potencia
máxima y, entonces, la variable dual asociada a la restricción de potencia máxima µig
g
tomará un valor distinto de cero (mientras que µi = 0 ) de forma que se verifique su
condición de optimalidad:
p+
∂p
⋅ qe = ci + µig
∂gi
(3.17)
Esto significa que si este grupo pudiese producir 1 MWh adicional, la empresa
obtendría un beneficio igual al valor de la variable dual de la restricción de potencia
máxima, dado por la diferencia entre el ingreso marginal y el coste marginal del grupo.
Análogamente, si un generador cuyo es mayor que su ingreso marginal está
produciendo, su restricción de potencia mínima está activa:
p+
∂p
g
⋅ qe = ci − µi
∂gi
(3.18)
g
Esta limitación supone un coste para la empresa dado por µi , ya que hace que parte
de la producción de la misma se genere con grupos más caros.
En el caso de un generador hidráulico, el coste variable de producción será igual a cero
( ci = 0 ) . Si no hay ninguna restricción de potencia activa, los generadores producirán
hasta que la variable dual de la restricción de gestión de las reservas hidráulicas sea
igual a su ingreso marginal:
p+
∂p
⋅ qe = µiH
∂gi
(3.19)
Esta variable dual µiH es el valor del agua, que representa cuánto cambia el valor de la
función objetivo, es decir, cuánto aumenta el beneficio de la empresa, cuando dispone
de 1 MWh adicional de energía hidráulica. Comprando esta ecuación con la
ecuación (3.14) que se obtuvo para un generador marginal térmico, se obtiene:
∂p

⋅ qe = ci 
∂gi


∂p
p+
⋅ qe = µiH 

∂gi
p+
40
⇒
µiH = ci
(3.20)
3.3 Formulación del problema del equilibrio del mercado
El valor del agua de una empresa será el coste variable del generador térmico que es
marginal o, en otras palabras, el coste variable del último generador térmico al que
sustituye. Si la empresa no tiene ningún generador marginal, sino que todos sus
grupos se encuentran funcionando en alguno de sus límites técnicos,
∂p

⋅ qe = ci + µig 
∂gi

⇒
∂p

p+
⋅ qe = µiH

∂gi
µiH = ci + µig
∂p
g
⋅ qe = ci − µi 
∂gi

⇒
∂p

p+
⋅ qe = µiH

∂gi
µiH = ci − µi
p+
(3.21)
p+
g
el valor del agua coincide con el coste variable del generador modificado por el coste
asociado a la restricción activa que impone algún límite a la producción de la empresa.
Considerar explícitamente el coste de la restricción activa en el cálculo del valor del
agua equivale al caso anterior, ya que cambia el coste variable del grupo, sumando o
restando la variable dual, y resultando el coste que tendría ese generador si no
estuviera activa su restricción.
Los comentarios sobre en qué condiciones los grupos térmicos se encuentran en sus
límites de producción máximo y mínimo son aplicables al funcionamiento de los
grupos hidráulicos reemplazando el concepto de coste marginal del grupo por el de
valor del agua del embalse.
p+
∂p
g
⋅ qe = µiH + µig − µi
∂gi
(3.22)
Si el ingreso marginal supera el valor del agua del embalse, el grupo hidráulico debe
( µ ≥ 0; µ = 0) ; en caso contrario, debe producir a
≥ 0) .
producir a potencia máxima
(
g
mínima potencia µig = 0; µi
g
i
g
i
Condición de complementariedad de holguras
Se añade la condición de complementariedad de holguras para completar el conjunto
de ecuaciones que define el problema de optimización de cada empresa.
41
3 Modelo de una etapa
• Limitación de potencia máxima de los generadores
 µig ⋅ ( gi − gi ) = 0

 gi − gi ≤ 0
 g
 µi ≥ 0
∀e, i ∈ e
(3.23)
• Limitación de potencia mínima de los generadores
(
)
µ g ⋅ g − g = 0
i
i
 i

 gi − gi ≤ 0
 g
 µi ≥ 0
∀e, i ∈ e
(3.24)
∀e, i ∈ ( e, ih )
(3.25)
• Gestión de las reservas hidráulicas
 µiH ⋅ ( gi − H i ) = 0

 gi − H i ≤ 0
 H
 µi ≥ 0
3.3.4
Formulación del equilibrio del mercado como un problema
mixto de complementariedad
El conjunto de todas las condiciones de optimalidad de todas las empresas forma el
problema mixto de complementariedad que define el problema del equilibrio del
mercado, tal y como se muestra en la Figura 3.3.
∂p
g
⋅ qe + p − ci − µig + µi − µiH = 0
∂gi
∀e, i ∈ e
 µig ⋅ ( gi − gi ) = 0

 gi − gi ≤ 0
 g
 µi ≥ 0
∀e, i ∈ e
(
)
µ g ⋅ g − g = 0
i
i
 i

 gi − gi ≤ 0
 g
 µi ≥ 0
42
∀e, i ∈ e
3.4 Equilibrio de Cournot
 µiH ⋅ ( gi − H i ) = 0

 gi − H i ≤ 0
 H
 µi ≥ 0
∀e, i ∈ ( e, ih )
(3.26)
3.4 Equilibrio de Cournot
Hasta este momento no se ha planteado el problema de cómo representar el
comportamiento de la demanda. En los modelos de explotación tradicionales, la
demanda se considera inelástica, es decir, que la cantidad total demandada es
independiente del precio y de las producciones de otras empresas. En el modelo de
Cournot las empresas compiten en un equilibrio de Nash considerando como única
variable estratégica la producción total ofertada al mercado.
En este modelo, los consumidores se representan mediante la curva de demanda
agregada, que relaciona el precio con la cantidad total producida por el sistema. Por
tanto, una vez que las empresas han decidido su producción, el precio es una variable
dependiente que puede obtenerse de la curva de demanda. La producción total del
mercado se puede formular como una función lineal del precio:
p = po − α ⋅ D 


D = ∑ qe

e
⇒
p = po − α ⋅ ∑ qe
(3.27)
e
La ecuación anterior se puede expresar como:


p = po − α ⋅  qe + ∑ qee 
ee≠ e


(3.28)
Según la ecuación (3.13), para calcular la cantidad que maximiza el beneficio de cada
empresa es necesario conocer la derivada del precio respecto de su producción. De este
modo, la derivada del precio respecto de la producción de un generador i
perteneciente a la empresa e queda:

∂q 
∂p
= −α ⋅  1 + ∑ ee 


∂gi
 ee ≠e ∂gi 
(3.29)
Así que es necesario conocer cómo varían las producciones de las empresas
competidoras cuando la empresa e modifica unitariamente la cantidad generada. Para
resolver el problema se introduce la llamada conjetura de Cournot, según la cual las
empresas competidoras no reaccionan ante cambios en la producción de una cierta
empresa. En consecuencia, la derivada de las cantidades de las demás empresas
respecto de la propia producción es nula. El mercado estará en equilibrio si ninguna
43
3 Modelo de una etapa
empresa obtiene beneficio adicional de cambiar la potencia que saca al mercado,
manteniéndose constantes las generaciones de las otras empresas. Esto implica, puesto
que debe mantenerse siempre el equilibrio entre generación y demanda, que debe ser
la demanda la que varíe su valor para responder al incremento en la potencia sacada al
mercado, por medio de la elasticidad demanda-precio. Así, un cambio en la potencia
generada supone un cambio en el precio del mercado y un cambio en el valor de la
demanda en ese periodo.
Entonces,
∂qee
=0
∂gi
⇒
∂p
= −α
∂gi
(3.30)
Es decir, la derivada del precio respecto de la producción de un generador es igual a la
pendiente de la curva de demanda para todas las empresas.
Sustituyendo los resultados de (3.30) en (3.26), el equilibrio del mercado queda:
g
p − α ⋅ qe − ci − µig + µi − µiH = 0
∀e, i ∈ e
 µig ⋅ ( gi − gi ) = 0

 gi − gi ≤ 0
 g
 µi ≥ 0
∀e, i ∈ e
(
)
µ g ⋅ g − g = 0
i
i
 i

 gi − gi ≤ 0
 g
 µi ≥ 0
∀e, i ∈ e
 µiH ⋅ ( gi − H i ) = 0

 gi − H i ≤ 0
 H
 µi ≥ 0
∀e, i ∈ ( e, ih )
(3.31)
3.5 Conclusiones
La experiencia real del proceso de liberalización que han vivido muchos de los
sistemas eléctricos de todo el mundo muestra que, con frecuencia, los mercados
eléctricos cuentan con un número reducido de empresas generadoras con un tamaño
considerable, lo que hace que las decisiones individuales de producción de los agentes
tengan un impacto significativo en el precio del mercado. En estas condiciones, las
empresas deciden su generación teniendo en cuenta el efecto global que tiene cada
44
3.5 Conclusiones
megavatio-hora producido sobre sus beneficios totales: si el beneficio obtenido por la
venta de 1 MWh adicional es mayor que la reducción de ingresos debida a la bajada de
precio correspondiente, que afecta a toda la potencia inframarginal de la compañía,
entonces la empresa decidirá sacar ese megavatio-hora al mercado; por el contrario, si
el impacto de la disminución del precio en el resto de producción de la empresa es más
importante que el margen que obtendría por el incremento de producción, la decisión
óptima será no aumentar la generación y mantener los precios en niveles más altos que
los que determinan sus costes variables de producción. Por tanto, las estrategias de
oferta de los agentes dependen de su coste marginal y de un término adicional
–respecto a los mercados en competencia perfecta– que es función de la derivada del
precio respecto a la producción de la empresa y de su potencia inframarginal.
En este problema, la decisión óptima de los agentes está definida por el equilibrio del
mercado, que puede calcularse mediante la resolución de un problema de
complementariedad. En este capítulo se han explicado los fundamentos de esta técnica
y se ha aplicado al cálculo del equilibrio estático de un mercado eléctrico de corto
plazo.
45
4
El modelo de Allaz y Vila
El análisis que se ha realizado en el capítulo anterior no tiene en cuenta la existencia de
mercados a plazo. Sin embargo, este tipo de mercados en los que los agentes pueden
negociar transacciones de energía cuya entrega tiene lugar en un periodo futuro son
una realidad en muchos de los mercados eléctricos existentes en la actualidad. Por
ejemplo, los mercados de PJM (Pennsylvania-New Jersey-Maryland), Francia,
Alemania, Holanda o NordPool (Noruega, Finlandia, Suecia y parte de Dinamarca),
entre otros, cuentan con mercados a plazo consolidados en los que se negocian
importantes volúmenes de energía. España representa, en este sentido, una excepción,
ya que hasta la reciente implantación del Mercado Ibérico de Electricidad (MIBEL) en
2006 no ha existido un mercado a plazo organizado de energía eléctrica. En este
contexto, surge la necesidad de estudiar la influencia que los mercados a plazo pueden
tener sobre el comportamiento estratégico de los agentes que operan en un mercado de
corto plazo o spot.
Este problema, aún sin resolver, está siendo objeto de estudio de numerosos trabajos de
investigación. Una de las principales referencias que se encuentran en la literatura es
Allaz y Vila (1993), donde se presenta un modelo en dos etapas para analizar el efecto
que tienen los contratos negociados en los mercados a plazo sobre las decisiones de los
agentes cuando operan en el mercado spot. En este capítulo se realiza una primera
aproximación al problema de la interacción entre los mercados a plazo y spot partiendo
del modelo desarrollado por Allaz y Vila.
47
4 El modelo de Allaz y Vila
4.1 Planteamiento
El modelo de Allaz y Vila considera dos únicas empresas que compiten en un mercado
a plazo y en un mercado spot. Se trata, por tanto, de un duopolio en el que las empresas
no compiten en condiciones de competencia perfecta, sino que tienen capacidad para
modificar el precio a través de sus decisiones. Estas dos compañías se comportan, tanto
en el mercado a plazo como en el spot, según el modelo de Cournot. Esto significa que
cada una de ellas decide su producción para maximizar su beneficio suponiendo que la
cantidad generada en cada mercado no depende de las decisiones de producción de la
otra empresa en ese mercado.
El modelo consta de dos etapas. En la primera etapa, las dos empresas generadoras
pueden participar en el mercado a plazo vendiendo energía que tiene fecha de entrega
en el segundo periodo. Los contratos de futuro negociados son firmes y las cantidades
contratadas son conocidas por todas las empresas tras el cierre del mercado a plazo. De
este modo, cada agente conoce, una vez que ha finalizado esta primera etapa, la
posición adquirida por la otra empresa en el mercado a plazo y puede tener en cuenta
esta información al tomar sus decisiones de producción en la siguiente etapa.
En la segunda etapa, las empresas deciden su producción en el spot según el modelo de
Cournot. Sin embargo, la existencia de un mercado anterior introduce algunas
diferencias respecto al modelo descrito en el capítulo 3:
• Por un lado, la función objetivo de cada empresa se ve modificada por las
posiciones a plazo que han adquirido previamente al negociar una cierta
cantidad de energía a plazo. En efecto, parte de la generación de las empresas ya
ha sido vendida y, por tanto, el precio que recibe esta producción ya es fijo. Sólo
la parte no negociada a plazo se remunera al precio resultante del spot.
• Por otro lado, cada empresa conoce la energía que ha negociado su competidora
en el mercado a plazo, por lo que es capaz de reaccionar en el spot a las decisiones
previas de la otra empresa.
Plantear el modelo en dos etapas diferenciadas es fundamental para representar la
naturaleza secuencial del problema. En los mercados a plazo se negocia la compra o
venta de energía en un periodo futuro a un precio determinado. En consecuencia, las
transacciones a plazo tienen lugar antes del momento de entrega de la energía
acordada, que coincide con un momento futuro en el que los agentes determinan su
producción total en el mercado spot. Luego, las decisiones de producción en cada
mercado no se toman de manera simultánea, sino que las empresas deciden primero la
cantidad que van a contratar a plazo –teniendo en cuenta los efectos de estos contratos
en el mercado spot– y, posteriormente, deciden la cantidad que van a producir
compitiendo en el mercado de corto plazo.
El modelo propuesto supone que no existe incertidumbre y que los agentes son capaces
de predecir perfectamente el precio de la energía en el mercado spot. Se ignoran, por
tanto, los efectos asociados a la gestión del riesgo de las empresas para centrase en el
48
4.1 Planteamiento
estudio del comportamiento estratégico de las empresas. Según Allaz y Vila, en estas
condiciones el precio de los contratos negociados en el mercado a plazo debe ser igual
al precio del mercado spot. Supóngase que una de las empresas se encuentra en la
primera etapa decidiendo qué cantidad de energía debe contratar a plazo. Esta
empresa tiene la posibilidad de vender una cantidad qc a un precio pc, que es superior a
sus costes de producción C y que, por tanto, le reportará un beneficio igual a
( pc ⋅ qc − C ) . Si el precio del spot p es superior al precio del contrato a plazo
( ps > pc ) , la empresa podría decidir contratar 1 MWh menos a plazo y venderlo
s
posteriormente en el spot al precio ps. Al hacerlo, recibiría un beneficio adicional igual a
la diferencia entre el precio del mercado spot y el precio del mercado a plazo
( ps − pc ) . Por tanto, al observar que obtiene un margen mayor por la venta de su
energía en el spot, la empresa iría reduciendo la cantidad vendida en el mercado a
plazo para venderla en la segunda etapa, y terminaría decidiendo no contratar a plazo.
Esto reduciría la cantidad ofertada en el mercado a plazo, haciendo que el precio de
este mercado suba. Análogamente, si el precio del spot fuese inferior al precio del
contrato a plazo
(p
s
)
< p c , la empresa obtendría mayores beneficios vendiendo su
energía en el mercado a plazo y decidiría no vender en el spot. Entonces, se reduciría la
oferta en el spot, lo que haría que el precio del mercado de corto plazo aumentase.
Por tanto, en ausencia de incertidumbre el precio del mercado a plazo no debe diferir
significativamente del precio del mercado spot. Si los agentes pueden predecir
perfectamente el precio spot, siempre tienen la posibilidad de vender más o menos
energía en el mercado de corto plazo de modo que escojan la opción que les reporte
mayores beneficios. Así, cuando los precios de los dos mercados se separan, las
empresas realizan una serie de operaciones buscando optimizar sus resultados que
tienden a igualar los dos precios.
De esta forma, los precios de los mercados a plazo y spot en el modelo serán iguales:
p s = pc = p
(4.1)
El precio viene dado por una función lineal de la demanda agregada del sistema de
pendiente unitaria:
p = po − D 

D = q1 − q2 
⇒
p = po − ( q1 + q2 )
(4.2)
donde q1 y q2 son las producción totales de las empresas 1 y 2, respectivamente.
Las curvas de coste no consideran explícitamente que cada empresa puede tener
diferentes grupos con distintos costes variables de producción, sino que se representan
simplificadamente como una función lineal de la producción de cada empresa. Estas
curvas son iguales para las dos empresas:
49
4 El modelo de Allaz y Vila
C1 = c ⋅ q1
(4.3)
C 2 = c ⋅ q2
(4.4)
donde C1 y C2 son los costes de producción de las empresas 1 y 2, respectivamente.
Esto es equivalente a suponer que toda la producción de cada empresa se produce con
un único generador de coste variable c.
4.2 Formulación del modelo
Para obtener las condiciones de optimalidad que definen el equilibrio del mercado es
necesario tener en cuenta dos conjuntos de ecuaciones: las de la primera etapa, que
modelan el comportamiento óptimo de las empresas cuando se encuentran decidiendo
sus contratos a plazo, y las de los problemas de optimización en el mercado spot. Este
apartado comienza analizando la segunda etapa.
4.2.1
Mercado spot
El objetivo de las empresas sigue siendo –tal y como se ha expuesto en el capítulo
anterior–, la maximización de sus beneficios, pero en este caso hay que tener en cuenta
que en esta segunda etapa parte de la producción ya ha sido contratada en el mercado
a plazo. La función objetivo de cada empresa queda, entonces:
(
)
para la empresa 1
(4.5)
(
)
para la empresa 2
(4.6)
max p s ⋅ q1 − q1c − c ⋅ q1
max p s ⋅ q2 − q2c − c ⋅ q2
Sustituyendo la ecuación (4.1):
(
)
para la empresa 1
(4.7)
(
)
para la empresa 2
(4.8)
max p ⋅ q1 − q1c − c ⋅ q1
max p ⋅ q2 − q2c − c ⋅ q2
El primer término de la función objetivo representa los ingresos que cada empresa
obtiene en el mercado spot. Este término no tiene en cuenta los ingresos asociados a las
posiciones a plazo q1c y q2c que cada agente ha adquirido en la etapa anterior puesto
que estas cantidades reciben el precio negociado previamente. El segundo término son
los costes de la producción total de las empresas, que sí incluyen las cantidades
contratadas a plazo ya que su fecha de entrega, es decir, el momento en el que deben
ser producidas, tiene lugar durante esta segunda etapa.
50
4.2 Formulación del modelo
Siguiendo la metodología descrita en el apartado 3.1, se construye la función
lagrangiana del problema de optimización de cada empresa:
L1 = p ⋅ ( q1 − q1c ) − c ⋅ q1
(4.9)
L2 = p ⋅ ( q2 − q2c ) − c ⋅ q2
(4.10)
Las condiciones de optimalidad del problema vienen dadas por la derivada del
lagrangiano respecto de las variables de decisión. En este caso, la única variable de
decisión que tiene cada empresa es la cantidad total de energía que van a generar, ya
que comportan según el modelo de Cournot –deciden su producción– y las cantidades
contratadas a plazo ya se han decidido con anterioridad. Por tanto,
(
)
(4.11)
(
)
(4.12)
∂L1 ∂p
=
⋅ q1 − q1c + p − c = 0
∂q1 ∂q1
∂L2 ∂p
=
⋅ q2 − q2c + p − c = 0
∂q2 ∂q2
De la ecuación (4.2) se tiene:
p = po − ( q1 + q2 )
 ∂p
 ∂q 
= − 1 + 2 

 ∂q1
 ∂q1 

 ∂p = −  ∂q1 + 1



 ∂q2

 ∂q2
⇒
(4.13)
y según lo descrito en el apartado 3.4,
∂q2

= 0
∂q1


∂q1
= 0
∂q2

⇒
 ∂p
 ∂q = −1
 1

 ∂p = −1
 ∂q2
(4.14)
Así, las condiciones de optimalidad quedan:
(
)
para la empresa 1
(4.15)
(
)
para la empresa 2
(4.16)
p − q1 − q1c − c = 0
p − q2 − q2c − c = 0
Estas ecuaciones forman, junto con la ecuación (4.2), el siguiente sistema de ecuaciones:
51
4 El modelo de Allaz y Vila
(
(
)
)
 p − q − qc − c = 0
1
1


c
 p − q2 − q2 − c = 0

 p = po − ( q1 + q2 )

(4.17)
Resultado 4.2.A
En el equilibrio, las producciones de las empresas y el precio del mercado están dados
por:
q1 =
po − c 2q1c − q2c
+
3
3
(4.18)
q2 =
po − c 2q2c − q1c
+
3
3
(4.19)
p=
po + 2c q1c + q2c
−
3
3
(4.20)
El precio del mercado spot depende de las cantidades de energía que las empresas han
negociado en el mercado a plazo. Un incremento en la cantidad contratada por alguna
de las empresas provoca una reducción del precio spot, mientras que un decremento de
la producción vendida a plazo hace que el precio del spot suba. Por tanto, los ingresos
que obtiene un agente en el mercado de corto plazo dependen de los contratos
negociados por el otro y, puesto que se ha definido que la información de la primera
etapa es pública, cada empresa puede reaccionar ante las decisiones de contratación de
la empresa competidora. Las ecuaciones anteriores recogen estas dependencias, de
forma que si un agente aumenta el volumen de sus contratos, el precio del mercado
baja y la otra empresa reacciona reduciendo su producción.
Demostración 4.2.A
(
(
)
)
 p − q − qc − c = 0
1
1


c
 p − q2 − q2 − c = 0

 p = po − ( q1 + q2 )

Sustituyendo la tercera ecuación del sistema en la primera:
(
)
po − ( q1 + q2 ) − q1 − q1c − c = 0
(
)
po − 2q1 + q2 − q1c − c = 0
52
4.2 Formulación del modelo
q2 = po − c − 2q1 + q1c
Al sustituir ahora en la segunda del sistema anterior se obtiene:
(
)
po − ( q1 + q2 ) − q2 − q2c − c = 0
(
)
po − q1 + 2q2 − q2c − c = 0
e incorporando la expresión obtenida para q2:
(
(
)
)
po − q1 + 2 ⋅ po − c − 2q1 + q1c − q2c − c = 0
(
)
po − 2 po − 2c − 3q1 + 2q1c − q2c − c = 0
− po + c + 3q1 − 2q1c + q2c = 0
po − c 2q1c − q2c
+
3
3
q1 =
La producción de la empresa 2 queda, entonces:
 p − c 2q1c − q2c
q2 = po − c − 2 ⋅  o
+
 3
3

 c
 + q1

q2 =
3 po − 3c − 2 po + 2c −4q1c + 2q2c + 3q1c
+
3
3
q2 =
po − c 2q2c − q1c
+
3
3
El precio del mercado se obtiene sustituyendo las expresiones calculadas para las producciones
de cada una de las empresas.
 p − c 2q1c − q2c po − c 2q2c − q1c
p = po −  o
+
+
+
 3
3
3
3

p=
3 po − 2 po + 2c q1c + q2c
−
3
3
p=
po + 2c q1c + q2c
−
3
3



53
4 El modelo de Allaz y Vila
4.2.2
Mercado a plazo
En la primera etapa, los agentes tienen como objetivo la maximización de sus
beneficios eligiendo el volumen de las transacciones a plazo que van a realizar. Al
tomar sus decisiones de contratación deben tener en cuenta que las cantidades de
energía contratadas en el mercado a plazo afectan también a los resultados que
obtendrán posteriormente en el spot. En otras palabras, el problema de las empresas en
la primera etapa es decidir la cantidad de contratos óptima que les reporta los mayores
beneficios globales. Por tanto, su función objetivo será maximizar los beneficios
obtenidos en las dos etapas:
(
)
para la empresa 1
(4.21)
(
)
para la empresa 2
(4.22)
max p c ⋅ q1c + p s ⋅ q1 − q1c − c ⋅ q1
max p c ⋅ q2c + p s ⋅ q2 − q2c − c ⋅ q2
Como se ha comentado, el modelo supone que los precios de los mercados a plazo y
spot son iguales. Entonces, las funciones objetivo quedan:
max p ⋅ q1 − c ⋅ q1
para la empresa 1
(4.23)
max p ⋅ q2 − c ⋅ q2
para la empresa 2
(4.24)
El lagrangiano de cada empresa es:
L1 = p ⋅ q1 − c ⋅ q1
(4.25)
L2 = p ⋅ q2 − c ⋅ q2
(4.26)
y teniendo en cuenta que la variable sobre la que pueden decidir los agentes en esta
etapa es su producción a plazo, las condiciones de optimalidad son:
∂L1
∂q1c
∂L2
∂q2c
=
=
∂p
∂q1c
∂p
∂q2c
⋅ q1 + p ⋅
⋅ q2 + p ⋅
∂q1
∂q1c
∂q2
∂q2c
−c⋅
−c⋅
∂q1
∂q1c
∂q2
∂q2c
=0
(4.27)
=0
(4.28)
De las expresiones que se obtuvieron al resolver el problema de optimización de la
segunda etapa se tiene que:
po − c 2q1c − q2c
q1 =
+
3
3
⇒
po − c 2q2c − q1c
+
3
3
⇒
q2 =
54
∂q1
∂q1c
∂q2
∂q2c
=
2
3
(4.29)
=
2
3
(4.30)
4.2 Formulación del modelo
p=
po + 2c q1c + q2c
−
3
3
1
 ∂p
 ∂q c = − 3
 1

 ∂p = − 1
 ∂q2c
3
⇒
(4.31)
 ∂q1c
ya que las empresas compiten según el modelo de Cournot 

c
 ∂q2
=
∂q2c
∂q1c

= 0 .


Resultado 4.2.B
Las condiciones de optimalidad de los problemas de optimización de las empresas en
la primera etapa forman el siguiente sistema de ecuaciones:
 po − c − 4q1c − q2c = 0

c
c
 po − c − 4q2 − q1 = 0
(4.32)
En el equilibrio, los contratos y producciones de las empresas y el precio de la energía
están definidos por el resultado del sistema de ecuaciones (4.32):
q1c = q2c =
q1 = q2 =
p=
po − c
5
(4.33)
2 ⋅ ( po − c )
(4.34)
5
po + 4c
5
(4.35)
Y el beneficio total de cada empresa es igual a:
B1 = B2 =
(
2 ⋅ po2 − 2 po c + c 2
)
(4.36)
25
Demostración 4.2.B
∂L1
∂q1c
∂L2
∂q2c
=
=
∂p
∂q1c
∂p
∂q2c
⋅ q1 + p ⋅
⋅ q2 + p ⋅
∂q1
∂q1c
∂q2
∂q2c
−c⋅
−c⋅
∂q1
∂q1c
∂q2
∂q2c
=0
=0
55
4 El modelo de Allaz y Vila
Sustituyendo (4.29), (4.30) y (4.31),
 1  p − c 2q c − q c
2
+ 1
− ⋅  o
3
 3  3

 1  po − c 2q2c − q1c
 − 3 ⋅  3 +
3


 2  po + 2c q1c + q2c
−
 + ⋅ 
3
 3  3
 2
 − c = 0
 3
 2  po + 2c q1c + q2c
−
 + ⋅ 
3
 3  3
 2
 − c = 0
 3
 − po + c + 2 po + 4c − 6c − 2q1c + q2c − 2q1c − 2q2c = 0

c
c
c
c
 − po + c + 2 po + 4c − 6c − 2q2 + q1 − 2q1 − 2q2 = 0
 po − c − 4q1c − q2c = 0

c
c
 po − c − 4q2 − q1 = 0
Despejando en la primera ecuación del sistema:
q2c = po − c − 4q1c
y sustituyendo en la segunda ecuación:
(
)
po − c − 4 ⋅ po − c − 4q1c − q1c = 0
po − c − 4 po + 4c + 16q1c − q1c = 0
−3 po + 3c + 15q1c = 0
q1c =
po − c
5
Entonces, la producción a plazo de la empresa 2 está dada por:
 p −c 
q2c = po − c − 4 ⋅  o

 5 
q2c =
5 po − 5c − 4 po + 4c
5
q2c =
po − c
5
Sustituyendo ahora en las ecuaciones (4.18) y (4.19):
p −c
q1 = o
+
3
q1 =
56
2
po − c po − c
−
5
5
3
5 po − 5c + 2 po − 2c − po + c
15
4.2 Formulación del modelo
2 ⋅ ( po − c )
q1 =
5
p −c
q2 = o
+
3
q2 =
q2 =
2
po − c po − c
−
5
5
3
5 po − 5c + 2 po − 2c − po + c
15
2 ⋅ ( po − c )
5
Y el precio de la energía (ecuación (4.20)) será:
p + 2c
−
p= o
3
po − c po − c
+
5
5
3
p=
5 po + 10c − po + c − po + c
15
p=
po + 4c
5
El beneficio total de las empresas es el beneficio obtenido en las dos etapas:
B1 = p ⋅ q1 − c ⋅ q1
B2 = p ⋅ q2 − c ⋅ q2
Sustituyendo las expresiones de las ecuaciones (4.34) y (4.35):
B1 = B2 =
2 ⋅ ( po − c )
po + 4c 2 ⋅ ( po − c )
⋅
−c⋅
5
5
5
B1 = B2 =
2 po2 + 8 po c − 2 po c − 8c 2 2 po c − 2c 2
−
25
5
B1 = B2 =
2 po2 + 6 po c − 8c 2 − 10 po c + 10c 2
25
B1 = B2 =
2 po2 + 6 po c − 8c 2 − 10 po c + 10c 2
25
B1 = B2 =
(
2 ⋅ po2 − 2 po c + c 2
)
25
57
4 El modelo de Allaz y Vila
4.3 Análisis de los resultados
Para analizar los resultados obtenidos en el juego en dos etapas, se comparará el caso
analizado en el apartado anterior con el problema de optimización de las empresas
suponiendo que no existe mercado a plazo y que los agentes sólo pueden vender su
producción en el mercado spot. Si la venta de energía se realiza en una única etapa, el
problema es equivalente al presentado en el capítulo 3, en el que las empresas sólo
compiten en el mercado de corto plazo.
Resultado 4.3.A
Si no existe un mercado a plazo, las producciones óptimas de las empresas son:
q1 = q2 =
po − c
3
(4.37)
y el precio de mercado queda:
p=
po + 2c
3
(4.38)
El beneficio de cada empresa será, entonces:
B1 = B2 =
po2 − 2 po c + c 2
9
(4.39)
Al comparar el beneficio que obtienen las empresas cuando negocian su energía en un
mercado a plazo y en un mercado spot (ecuación (4.36)) con lo que obtienen al vender
su producción solamente en el mercado de corto plazo (ecuación (4.39)), se observa que
los resultados de las empresas empeoran cuando contratan parte de su energía a
futuro.
(
2 ⋅ po2 − 2 po c + c 2
)
25
beneficio con mercado a plazo
<
po2 − 2 po c + c 2
9
(4.40)
beneficio sin mercado a plazo
Luego, si el beneficio que obtienen las empresas cuando negocian en un mercado a
plazo es menor que el que resulta cuando operan únicamente en el mercado spot, cabe
preguntarse por qué los agentes querrían participar en un mercado a plazo. Pues bien,
supóngase ahora que existe un mercado a plazo, pero que sólo la empresa 1 participa
en él. En este caso, el problema de optimización de la primera etapa se plantea
únicamente para la empresa 1.
Resultado 4.3.B
El equilibrio del problema cuando el único agente que participa en el mercado a plazo
es la empresa 1 está definido por:
58
4.3 Análisis de los resultados
q1c =
po − c
4
q1 =
po − c
;
2
p=
po + 3c
4
(4.41)
q2 =
po − c
4
(4.42)
(4.43)
Los beneficios que obtienen cada una de las empresas en este caso son:
B1 =
po2 − 2 po c + c 2
;
8
B2 =
po2 − 2 po c + c 2
16
(4.44)
De modo que, cuando sólo uno de los agentes tiene la oportunidad de negociar a plazo,
los beneficios que obtiene mejoran frente a los que tendría si no lo hiciera. En cambio,
los resultados de la segunda empresa son notablemente inferiores a los del caso en el
que ningún agente contrata a plazo. Estos resultados son similares a los que se
obtienen en el modelo de Stackelberg4, en el que las ofertas no se realizan
simultáneamente. En este caso, la empresa 1 decide su producción a plazo,
adquiriendo un compromiso de venta que le hace estar menos expuesta al precio spot.
Por el contrario, toda la producción de la empresa 2 recibirá el precio spot, así que este
agente tiene más incentivos que el primero para mantener el precio alto. Cuando,
posteriormente, la empresa 2 selecciona la cantidad óptima que debe generar, lo hace
en función de la energía contratada por la empresa 1, teniendo en cuenta la menor
exposición que tiene ésta al precio. Por tanto, si la empresa 1 se adelanta, es capaz de
mejorar sus resultados capturando mayor cuota de mercado, ya que la otra empresa
actuará condicionada por su decisión retirando cantidad para mantener un precio spot
algo más elevado. Entonces, la empresa 2 también querrá participar en el mercado a
plazo en un intento por conseguir los mismos resultados que la empresa 1. Ambos
productores tienen incentivos estratégicos para contratar parte de su energía a plazo.
Sin embargo, cuando los dos agentes negocian contratos de futuro, los resultados de
ambos se reducen respecto al caso en el que sólo existe un mercado spot. Negociar en el
mercado a plazo representa un dilema del prisionero para las dos empresas: cuando
uno de los productores consigue ser el único que contrata a plazo, obtiene un
considerable aumento de sus beneficios; en cambio, cuando las dos empresas
participan en el mercado a plazo, las dos obtienen peores resultados.
4
Véase el capítulo 2.
59
4 El modelo de Allaz y Vila
Demostración 4.3.A
El problema del equilibrio de un único mercado spot queda definido por la siguiente función
objetivo para cada empresa:
max p ⋅ q1 − c ⋅ q1
para la empresa 1
max p ⋅ q2 − c ⋅ q2
para la empresa 2
donde p = po − ( q1 + q2 ) es el precio de mercado
Construyendo el lagrangiano y derivando respecto a la producción de cada empresa:
p ⋅ q1 − c ⋅ q1
⇒
∂L1
∂p
=
⋅ q1 + p − c = 0
∂q1 ∂q1
= p ⋅ q2 − c ⋅ q2
⇒
∂L2
∂p
=
⋅ q2 + p − c = 0
∂q2
∂q2
L1 =
L2
donde
∂p
∂p
=
= −1
∂q1 ∂q2
Así, las condiciones de optimalidad que definen el equilibrio son:
p − q1 − c = 0
p − q2 − c = 0
De las condiciones de optimalidad anteriores y la ecuación del precio se obtienen el siguiente
sistema de ecuaciones:
 p − q1 − c = 0

 p − q2 − c = 0
p = p − q +q
o ( 1
2)

Sustituyendo la tercera ecuación del sistema en la primera:
po − ( q1 + q2 ) − q1 − c = 0
po − ( 2q1 + q2 ) − c = 0
q2 = po − c − 2q1
Sustituyendo ahora la ecuación del precio en la segunda ecuación del sistema:
po − ( q1 + q2 ) − q2 − c = 0
po − ( q1 + 2q2 ) − c = 0
60
4.3 Análisis de los resultados
e, incorporando la expresión obtenida para q2:
po − ( q1 + 2 ( po − c − 2q1 ) ) − c = 0
po − 2 po + 2c − c + 3q1 = 0
po − c
3
q1 =
La producción de la empresa 2 queda:
q2 = po − c − 2
po − c
3
q2 =
3 po − 3c − 2 po + 2c
3
q2 =
po − c
3
El precio del mercado queda definido por las producciones de las empresas:
 p − c po − c 
p = po −  o
+
3 
 3
p=
3 po − 2 po + 2c
3
p=
po + 2c
3
El beneficio de cada empresa es:
B1 = p ⋅ q1 − c ⋅ q1
B2 = p ⋅ q2 − c ⋅ q2
que, en este caso queda:
B1 = B2 =
po + 2c po − c
p −c
⋅
−c⋅ o
3
3
3
B1 = B2 =
po2 + 2 po c − po c − 2c 2 po c − c 2
−
9
3
B1 = B2 =
po2 + po c − 2c 2 − 3 po c + 3c 2
9
B1 = B2 =
po2 − 2 po c + c 2
9
61
4 El modelo de Allaz y Vila
Demostración 4.3.B
Si la empresa 1 es la única que puede participar en el mercado a plazo, el problema de
optimización de la primera etapa se plantea sólo para este agente. La función objetivo será:
max p ⋅ q1 − c ⋅ q1
y
L1 = p ⋅ q1 − c ⋅ q1
Luego, la condición de optimalidad que define el equilibrio del mercado es:
∂L1
∂q1c
=
∂p
∂q1c
donde q1 =
po − c 2q1c
+
3
3
p=
po + 2c q1c
−
3
3
⋅ q1 + p ⋅
∂q1
∂q1c
−c⋅
∂q1
⇒
∂q1c
∂p
⇒
∂q1c
∂q1
∂q1c
=
=0
2
3
=−
1
3
Por tanto,
1  p − c 2q1c
− ⋅ o
+
3  3
3
 2  po + 2c q1c
−
 + ⋅ 
3
 3  3
− po + c + 2 po + 4c − 6c − 2q1c − 2q1c = 0
po − c − 4q1c = 0
q1c =
po − c
4
Las producciones totales de cada empresa serán:
q1 =
po − c 2q1c
+
3
3
po − c
po − c 2 4
q1 =
+
3
3
62
q1 =
4 po − 4c + 2 po − 2c
12
q1 =
po − c
2
 2
 − c = 0
 3
4.3 Análisis de los resultados
po − c q1c
−
3
3
q2 =
p −c
q2 = o
−
3
po − c
4
3
q2 =
4 po − 4c − po + c
12
q2 =
po − c
4
y el precio de mercado:
po + 2c q1c
−
3
3
p=
p + 2c
p= o
−
3
po − c
4
3
p=
4 po + 8c − po + c
12
p=
po + 3c
4
Los beneficios que obtienen cada una de las empresas son:
B1 = p ⋅ q1 − c ⋅ q1
B1 =
po + 3c po − c
p −c
⋅
−c⋅ o
4
2
2
B1 =
po2 − po c + 3 po c − 3c 2 po c − c 2
−
8
2
B1 =
po2 + 2 po c − 3c 2 − 4 po c + 4c 2
8
B1 =
po2 − 2 po c + c 2
8
B2 = p ⋅ q2 − c ⋅ q2
B2 =
po + 3c po − c
p −c
⋅
−c⋅ o
4
4
4
B2 =
po2 − po c + 3 po c − 3c 2 po c − c 2
−
16
4
63
4 El modelo de Allaz y Vila
B2 =
po2 + 2 po c − 3c 2 − 4 po c + 4c 2
16
B2 =
po2 − 2 po c + c 2
16
Según los resultados del modelo, los mercados a plazo afectan de una manera nada
obvia al comportamiento de los agentes en el mercado spot. Las condiciones de
optimalidad del problema de optimización de la segunda etapa (ecuaciones (4.15) y
(4.16)) en el que las empresas deciden su producción total conocidas tanto su posición a
plazo como la de su competidora, eran:
(
)
p − qe − qec − c = 0
En esta ecuación, la cantidad negociada a plazo minora la producción total de la
( (
empresa. El ingreso marginal de la empresa p − qe − qec
) ) difiere del ingreso marginal
del modelo de una etapa ( p − qe ) , ya que el decremento de precio que implica la venta
de 1 MWh adicional no afecta al ingreso de las ventas a plazo, que reciben un precio
que ya es fijo. Por tanto, cuando un agente con parte de su energía contratada se
plantea la posibilidad de vender 1 MWh más en el spot debe comparar las dos áreas
sombreadas de la siguiente figura:
ps
∆ps
Coste de producción
Precio de la energía
qec
∆qe
q
Figura 4.1: Efectos del incremento de producción sobre el beneficio de una empresa con contratos a plazo
• El área verde que representa los beneficios que obtiene la empresa al incrementar
unitariamente su producción es igual al de la Figura 3.5 del modelo de una etapa
analizado en el capítulo 3.
• En cambio, el área roja que representa la reducción del beneficio asociada al
decremento en el precio spot es menor, ya que sólo afecta a la energía que no ha
sido vendida previamente en el mercado a plazo. Así que contratar parte de su
energía a plazo hace que los agentes sean menos sensibles a variaciones en el
64
4.4 Conclusiones
precio spot y, por tanto, sean menos dependientes de la elasticidad del precio ante
un incremento en su producción.
Allaz y Vila concluyen que la existencia de mercados a plazo mejora el nivel de
competencia. Aunque el mercado mantenga una estructura oligopolista, los contratos a
plazo tienen un efecto procompetitivo, ya que reducen los incentivos de las empresas
para ejercer su poder de mercado y, con ello, se acercan a las condiciones de
competencia perfecta. Estos resultados sugieren que los mercados a plazo podrían
emplearse como herramientas encaminadas a limitar el poder de mercado de los
agentes.
4.4 Conclusiones
El resultado fundamental del modelo de Allaz y Vila es la identificación de un efecto
procompetitivo asociado a la existencia de mercados a plazo. El modelo muestra que
contratar parte de su generación a futuro hace que las empresas modifiquen su
comportamiento en el mercado spot, adoptando estrategias de oferta más agresivas que
conllevan producciones más elevadas y menores precios de mercado. El mercado spot
mejora, entonces, su nivel de competencia. Este efecto se debe a que el ingreso
( (
marginal de las compañías p − qe − qec
) ) aumenta con la cantidad contratada a plazo y,
por tanto, los agentes obtienen beneficios adicionales al incrementar su producción. En
efecto, el volumen de energía negociada a plazo minora la potencia inframarginal de la
empresa, que observa que las variaciones del precio spot no afectan a la parte de la
generación que ha sido negociada previamente –que recibe el precio fijado en la etapa
anterior–. El impacto de una bajada de precio sobre los beneficios de la potencia de la
empresa que se encuentra produciendo es menor que en el juego de una etapa, de
modo que los agentes son menos sensibles a la elasticidad del precio y tienden a
aumentar su producción. Por tanto, la existencia de un mercado a plazo anterior al spot
reduce los incentivos de los agentes para ejercer su poder de mercado.
Este resultado nada intuitivo del modelo de Allaz y Vila implica que las empresas
obtienen menores beneficios cuando deciden realizar transacciones a plazo. La
justificación para que, a pesar de lo anterior, las compañías negocien contratos es que
la posibilidad de operar en mercados a plazo crea un dilema del prisionero para los
agentes. Cuando las dos empresas se contratan a futuro, sus resultados empeoran
respecto al caso en el que no participan en el mercado a plazo. Sin embargo, si uno de
los agentes no se contrata, entonces la otra empresa tiene fuertes incentivos para
realizar ventas a plazo, ya que de este modo incrementaría sus beneficios. Como
consecuencia, los resultados de la primera empresa se reducirían notablemente. De
modo que ambos productores tienen importantes incentivos para negociar parte de su
producción a plazo pero, si los dos lo hacen, su situación empeora respecto a haber
operado exclusivamente en el mercado spot.
65
5
Generalización del modelo
de Allaz y Vila
El modelo de Allaz y Vila define una serie de parámetros como datos del problema
que, en general, no se adaptan a la realidad de los mercados eléctricos existentes. Esto
limita enormemente las posibles aplicaciones del modelo, ya que no se puede emplear
para realizar estudios realistas sobre la base de algún mercado conocido. En este
capítulo se presenta una generalización del modelo descrito en el capítulo anterior, que
extiende su formulación a un caso de mercado menos rígido que el considerado por
Allaz y Vila.
67
5 Generalización del modelo de Allaz y Vila
5.1 Planteamiento
El estudio de Allaz y Vila sobre la interacción entre mercados a plazo y mercados al
contado está desarrollado para unas condiciones de mercado muy particulares. El
modelo considera la existencia de dos únicas empresas con idénticas curvas de coste.
Estas curvas están representadas por funciones lineales de la producción de cada
empresa, lo que equivale a considerar que cada una de ellas es propietaria de un único
generador que produce toda la energía de la compañía sin ninguna restricción de
capacidad. Además, el precio viene dado por una función lineal de la demanda de
pendiente unitaria.
Sin embargo, estas condiciones no se cumplen en la mayoría de los mercados eléctricos
existentes. En el siguiente apartado se presenta una generalización del modelo de Allaz
y Vila, que extiende el estudio para el caso en el que opera un número E indeterminado
de empresas con costes Ce –que, en general, serán distintos para las diferentes
compañías de generación– e incorpora una función lineal general con pendiente α para
representar el precio de mercado.
p = po − α ⋅ D 


D = ∑ qe

e
⇒
p = po − α ⋅ ∑ qe
(5.1)
e
En el apartado 5.2 se mantienen las hipótesis fundamentales del modelo de Allaz y
Vila: se plantea un juego en dos etapas en el que las empresas compiten en un mercado
a plazo y, posteriormente, en un mercado spot, comportándose en cada uno de ellos
según el modelo de Cournot. Además, se considera que los agentes son capaces de
predecir perfectamente el precio spot y que los precios de los dos mercados son iguales
( p s = pc = p ) . Los resultados de la primera etapa son conocidos por todos los agentes
que participan en el mercado de corto plazo, de manera que pueden tener en cuenta las
posiciones a plazo adquiridas por todas las empresas e incorporar esta información en
el proceso de toma de decisiones en el spot.
5.2 Formulación del modelo
5.2.1
Mercado spot
La función objetivo para cada una de las empresas que compiten en el mercado spot
está dada por:
(
)
max p s ⋅ qe − qec − Ce
∀e
donde ps es el precio del mercado spot, p s = p = po − α ⋅
(5.2)
∑ qe ,
e
68
5.2 Formulación del modelo
qe es la producción total de la empresa e,
qec es la producción contratada a plazo por la empresa e,
Ce es el coste de producción de la empresa e, que será función de qe.
Los ingresos de la función objetivo no tienen en cuenta la producción vendida a plazo,
que recibe el precio negociado en primera etapa.
El lagrangiano del problema de optimización de cada empresa es:
Le = p ⋅ ( qe − qec ) − Ce
∀e
(5.3)
Las condiciones de optimalidad que definen el comportamiento óptimo de los agentes
se obtienen derivando la función lagrangiana respecto de la variable de decisión de la
empresa (su producción total):
(
)
∂Le ∂p
∂C
=
⋅ qe − qec + p − e = 0
∂qe ∂qe
∂qe
∀e
(5.4)
De la ecuación del precio (ecuación (5.1)),
p = po − α ⋅ ∑ qe
⇒
e

∂q 
∂p
= −α ⋅  1 + ∑ ee 
∂qe
 ee ≠e ∂qe 
(5.5)
e, introduciendo la conjetura de Cournot,
∂p
= −α
∂qe
(5.6)
Por tanto, la ecuación de optimalidad de cada empresa queda:
(
)
p − α ⋅ qe − qec −
∂Ce
=0
∂qe
∀e
(5.7)
Entonces, se puede plantar un sistema de E+1 ecuaciones formado por las E
condiciones de optimalidad anteriores, una para cada una de las empresas, y por la
ecuación (5.1) que define el precio de mercado.
69
5 Generalización del modelo de Allaz y Vila
(
)
(
)
(
)
∂C1

c
 p − α ⋅ q1 − q1 − ∂q = 0
1

∂C2

c
 p − α ⋅ q2 − q2 − ∂q = 0
2


∂
C
c
3
=0
 p − α ⋅ q3 − q3 −
∂
q
3

⋮

 p − α ⋅ q − q c − ∂Ce−1 = 0
e−1
e−1

∂qe−1


∂C
 p − α ⋅ qe − qec − e = 0
∂qe

⋮

∂CE −1

c
=0
 p − α ⋅ qE −1 − qE −1 − ∂q
E −1


∂CE
c
 p − α ⋅ qE − qE − ∂q = 0
E

 p = po − α ⋅ ( q1 + q2 + q3 + … + qe −1 + qe + … + qE −1 + qE )

(
)
(
)
(
)
(
)
(5.8)
Resultado 5.2.A
Resolviendo el sistema de ecuaciones anterior se obtiene que, en el equilibrio, las
producciones de todas las empresas y el precio del mercado están dados por las
siguientes expresiones:
po − E ⋅
qe =
( E + 1) ⋅ α
po + ∑
p=
∂Ce
∂Cee
+∑
∂qe ee≠e ∂qee
e
∂Ce
qe
( E + 1)
E ⋅ qec −
+
∑ qeec
ee ≠e
( E + 1)
∀e
(5.9)
α ⋅ ∑ qec
−
e
( E + 1)
(5.10)
Es fácil comprobar que para el caso en el que sólo compiten dos empresas ( E = 2 ) con
costes iguales a una función lineal de la producción de la empresa de pendiente c
( Ce = c ⋅ qe ) y la curva del precio tiene pendiente unitaria (α = 1) , las expresiones
anteriores toman los mismos valores que se obtuvieron en el capítulo 4.
70
5.2 Formulación del modelo
Demostración 5.2.A
(
)
(
)
(
)
∂C1

c
 p − α ⋅ q1 − q1 − ∂q = 0
1


∂
C
c
2
=0
 p − α ⋅ q2 − q2 −
∂q2


∂C3
c
=0
 p − α ⋅ q3 − q3 −
∂q3

⋮

∂Ce −1

c
=0
 p − α ⋅ qe −1 − qe −1 − ∂q
e −1


∂C
 p − α ⋅ qe − qec − e = 0
∂qe

⋮


∂CE −1
c
=0
 p − α ⋅ qE −1 − qE −1 −
∂qE −1


∂CE
c
=0
 p − α ⋅ qE − qE −
∂qE

 p = p − α ⋅(q + q + q +… + q + q +… + q
o
1
2
3
e −1
e
E −1 + q E )

(
)
(
)
(
)
(
)
Sustituyendo en la primera ecuación del sistema la expresión del precio del mercado definida por
la última ecuación:
(
)
po − α ⋅ ( q1 + q2 + q3 + … + qe −1 + qe + … + qE −1 + qE ) − α ⋅ q1 − q1c −
(
)
po − α ⋅ 2q1 + q2 + q3 + … + qe −1 + qe + … + qE −1 + qE − q1c −
po −
q2 =
∂C1
∂q1
α
∂C1
=0
∂q1
∂C1
=0
∂q1
− 2q1 − q3 − … − qe −1 − qe − … − qE −1 − qE + q1c
Se sustituye ahora la ecuación del precio en la segunda ecuación del sistema y, posteriormente, se
incorpora la expresión obtenida para q2 :
(
)
po − α ⋅ ( q1 + q2 + q3 + … + qe −1 + qe + … + qE −1 + qE ) − α ⋅ q2 − q2c −
(
)
po − α ⋅ q1 + 2q2 + q3 + … + qe −1 + qe + … + qE −1 + qE − q2c −
∂C2
=0
∂q2
∂C2
=0
∂q2
71
5 Generalización del modelo de Allaz y Vila


∂C 
2  po − 1 

∂q1 
po − α ⋅  q1 + 
− 4q1 − 2q3 − … − 2qe −1 − 2qe − … − 2qE −1 − 2qE + 2q1c +

α





c  ∂C2
+ q3 + … + qe −1 + qe + … + qE −1 + qE − q2 −
=0
 ∂q
2



 
∂C1 
 2  po −

∂q1 
po − α ⋅  
− 3q1 − q3 − … − qe −1 − qe − … − qE −1 − qE +

α





∂C
+2q1c − q2c  − 2 = 0
 ∂q
2



− po + 2
(
)
∂C1 ∂C2
−
+ α ⋅ 3q1 + q3 + … + qe −1 + qe + … + qE −1 + qE − 2q1c + q2c = 0
∂q1 ∂q2
po − 2
q3 =
∂C1 ∂C2
+
∂q1 ∂q2
α
− 3q1 − … − qe −1 − qe − … − qE −1 − qE + 2q1c − q2c
Sustituyendo en la ecuación 3:
(
)
po − α ⋅ ( q1 + q2 + q3 + … + qe −1 + qe + … + qE −1 + qE ) − α ⋅ q3 − q3c −
(
)
po − α ⋅ q1 + q2 + 2q3 + … + qe −1 + qe + … + qE −1 + qE − q3c −
∂C3
=0
∂q3
∂C3
=0
∂q3
Incorporando la expresión obtenida para q2 :
∂C

po − 1

∂q1
po − α ⋅  q1 +
− 2q1 − q3 − … − qe −1 − qe − … − qE −1 − qE + q1c +
α





∂C
+2q3 + … + qe−1 + qe + … + qE −1 + qE − q3c  − 3 = 0
 ∂q
3



72
5.2 Formulación del modelo
∂C1


 po − ∂q
 ∂C
1
po − α ⋅ 
− q1 + q3 + q1c − q3c  − 3 = 0
α

 ∂q3




Y sustituyendo q3 según la ecuación que se obtuvo anteriormente:
∂C1
∂C ∂C

po − 2 1 + 2
 po − ∂q
∂q1 ∂q2
1
po − α ⋅ 
− q1 +
− 3q1 − … − qe −1 − qe − … − qE −1 − qE +
α
α





∂C
+2q1c − q2c + q1c − q3c  − 3 = 0
 ∂q
3



∂C1 ∂C2

 2 po − 3 ∂q + ∂q
1
2
po − α ⋅ 
− 4q1 − … − qe −1 − qe − … − qE −1 − qE +
α





∂C
+3q1c − q2c − q3c  − 3 = 0
 ∂q
3



− po + 3
∂C1 ∂C2 ∂C3
−
−
+ α ⋅ ( 4q1 + … + qe−1 + qe + … + qE −1 + qE −
∂q1 ∂q2 ∂q3
)
−3q1c + q2c + q3c = 0
po − 3
q4 =
∂C1 ∂C2 ∂C3
+
+
∂q1 ∂q2 ∂q3
α
− 4q1 − … − qe −1 − qe − … − qE −1 − qE + 3q1c − q2c − q3c
Se repite el proceso y al llegar a la ecuación e-1 se tiene:
(
)
po − α ⋅ ( q1 + q2 + q3 + … + qe −1 + qe + … + qE −1 + qE ) − α ⋅ qe−1 − qec−1 −
(
)
po − α ⋅ q1 + q2 + q3 + … + 2qe −1 + qe + … + qE −1 + qE − qec−1 −
∂Ce −1
=0
∂qe −1
∂Ce −1
=0
∂qe −1
73
5 Generalización del modelo de Allaz y Vila
Sustituyendo q2 :
∂C

po − 1

∂q1
po − α ⋅  q1 +
− 2q1 − q3 − … − qe −1 − qe − … − qE −1 − qE + q1c +
α





∂C
+ q3 + … + 2qe −1 + qe + … + qE −1 + qE − qec−1  − e −1 = 0
 ∂q
e −1



∂C1


 po − ∂q
 ∂C
1
po − α ⋅ 
− q1 + qe −1 + q1c − qec−1  − e −1 = 0
α

 ∂qe−1




Se sustituye qe−1 , cuya expresión se habrá obtenido en el paso anterior al sustituir en la
ecuación e-2:
∂C
∂C
∂C ∂C
∂C1

po − ( e − 2 ) ⋅ 1 + 2 + 3 + … + e − 2
 po − ∂q
∂
q
∂
q
∂
q
∂qe − 2
1
1
2
3
po − α ⋅ 
− q1 +
−
α
α



− ( e − 1) ⋅ q1 − qe − … − qE −1 − qE + ( e − 2 ) ⋅ q1c − q2c − q3c − … − qec− 2 +


c
c  ∂Ce −1
+ q1 − qe −1 −
=0
 ∂q
e −1



∂Ce − 2
∂C1 ∂C2 ∂C3

 2 po − ( e − 1) ⋅ ∂q + ∂q + ∂q + … + ∂q
1
2
3
e− 2
po − α ⋅ 
− e ⋅ q1 − qe − … − qE −1 − qE +

α




∂C
+ ( e − 1) ⋅ q1c − q2c − q3c − … − qec−1  − e −1 = 0
 ∂q
e −1



− po + ( e − 1) ⋅
(
∂C
∂C1 ∂C2 ∂C3
−
−
− … − e −1 +
∂q1 ∂q2 ∂q3
∂qe −1
)
+α ⋅ e ⋅ q1 + qe + … + qE −1 + qE − ( e − 1) ⋅ q1c + q2c + q3c + … + qec−1 = 0
qe =
po − ( e − 1) ⋅
∂C
∂C1 ∂C2 ∂C3
+
+
+ … + e −1
∂q1 ∂q2 ∂q3
∂qe −1
α
−
−e ⋅ q1 − qe +1 − … − qE −1 − qE + ( e − 1) ⋅ q1c − q2c − q3c − … − qec−1
74
5.2 Formulación del modelo
Sustituyendo en la ecuación E-1:
(
)
po − α ⋅ ( q1 + q2 + q3 + … + qe −1 + qe + … + qE −1 + qE ) − α ⋅ qE −1 − qEc −1 −
(
)
po − α ⋅ q1 + q2 + q3 + … + qe −1 + qe + … + 2qE −1 + qE − qEc −1 −
∂CE −1
=0
∂qE −1
∂CE −1
=0
∂qE −1
Se incorpora q2 :
∂C

po − 1

∂q1
po − α ⋅  q1 +
− 2q1 − q3 − … − qe −1 − qe − … − qE −1 − qE + q1c +
α





∂C
+ q3 + … + qe −1 + qe + … + 2qE −1 + qE − qEc −1  − E −1 = 0
 ∂q
E −1



∂C1


 po − ∂q
 ∂C
c
c
1
po − α ⋅ 
− q1 + qE −1 + q1 − qE −1  − E −1 = 0
α

 ∂qE −1




Se sustituye qE −1 :
∂C1

 po − ∂q
1
po − α ⋅ 
− q1 +
α



∂C ∂C
∂C
∂C
∂C
∂C
po − ( E − 2 ) ⋅ 1 + 2 + 3 + … + e −1 + e + … + E − 2
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE − 2
+
−
α
− ( E − 1) ⋅ q1 − qE + ( E − 2 ) ⋅ q1c − q2c − q3c − … − qec−1 − qec − … − qEc − 2 +


∂C
+ q1c − qEc −1  − E −1 = 0
 ∂q
E −1



75
5 Generalización del modelo de Allaz y Vila
∂Ce −1 ∂Ce
∂C1 ∂C2 ∂C3
∂C

+
+ … + E −2
 2 po − ( E − 1) ⋅ ∂q + ∂q + ∂q + … + ∂q
∂
q
∂qE − 2
1
2
3
e −1
e
po − α ⋅ 
−

α




∂C
− E ⋅ q1 − qE + ( E − 1) ⋅ q1c − q2c − q3c − … − qec−1 − qec − … − qEc −1  − E −1 = 0
 ∂q
E −1



− po + ( E − 1) ⋅
(
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
−
−
− … − e −1 − e − … − E −1 +
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1
)
+α ⋅ E ⋅ q1 + qE − ( E − 1) ⋅ q1c + q2c + q3c + … + qec−1 + qec + … + qEc −1 = 0
qE =
po − ( E − 1) ⋅
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
+
+
+ … + e −1 + e + … + E −1
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1
α
−
− E ⋅ q1 + ( E − 1) ⋅ q1c − q2c − q3c − … − qec−1 − qec − … − qEc −1
Por último, sustituyendo ahora en la ecuación E:
(
)
po − α ⋅ ( q1 + q2 + q3 + … + qe −1 + qe + … + qE −1 + qE ) − α ⋅ qE − qEc −
(
)
po − α ⋅ q1 + q2 + q3 + … + qe −1 + qe + … + qE −1 + 2qE − qEc −
∂CE
=0
∂qE
∂CE
=0
∂qE
Sustituyendo q2 :
∂C

po − 1

∂q1
po − α ⋅  q1 +
− 2q1 − q3 − … − qe −1 − qe − … − qE −1 − qE + q1c +
α





∂C
+ q3 + … + qe −1 + qe + … + qE −1 + 2qE − qEc  − E = 0
 ∂q
E



∂C1


 po − ∂q
 ∂C
c
c
1
po − α ⋅ 
− q1 + qE + q1 − qE  − E = 0
α

 ∂qE




76
5.2 Formulación del modelo
Y sustituyendo qE :
∂C1

 po − ∂q
1
po − α ⋅ 
− q1 +
α



∂C ∂C
∂C
∂C
∂C
∂C
po − ( E − 1) ⋅ 1 + 2 + 3 + … + e −1 + e + … + E −1
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1
+
−
α
− E ⋅ q1 + ( E − 1) ⋅ q1c − q2c − q3c − … − qec−1 − qec − … − qEc −1 +


∂C
+ q1c − qEc  − E = 0
 ∂q
E



∂Ce −1 ∂Ce
∂C1 ∂C2 ∂C3
∂C

+
+ … + E −1
 2 po − E ⋅ ∂q + ∂q + ∂q + … + ∂q
∂qe
∂qE −1
1
2
3
e −1
po − α ⋅ 
−

α




c
c
c
c
c
c
c  ∂C E
− ( E + 1) ⋅ q1 + E ⋅ q1 − q2 − q3 − … − qe −1 − qe − … − qE −1 − qE −
=0
 ∂q
E



− po + E ⋅
(
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
∂C
−
−
− … − e −1 − e − … − E −1 − E +
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE
)
+α ⋅ ( E + 1) ⋅ q1 − E ⋅ q1c + q2c + q3c + … + qec−1 + qec + … + qEc −1 + qEc = 0
po − E ⋅
q1 =
+
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
∂C
+
+
+ … + e −1 + e + … + E −1 + E
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE
+
( E + 1) ⋅ α
E ⋅ q1c − q2c − q3c − … − qec−1 − qec − … − qEc −1 − qEc
( E + 1)
Una vez que se ha obtenido una ecuación para q1 que es función únicamente de las producciones
contratadas por todas las empresas, se sustituye progresivamente en las expresiones de las
producciones totales de cada agente que se han ido calculando.
Así, sustituyendo q1 en la expresión obtenida para qE :
77
5 Generalización del modelo de Allaz y Vila
qE =
po − ( E − 1) ⋅
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
+
+
+ … + e −1 + e + … + E −1
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1
α
−
∂C1 ∂C2 ∂C3
∂Ce −1 ∂Ce
∂C
∂C

+
+ … + E −1 + E
 po − E ⋅ ∂q + ∂q + ∂q + … + ∂q
∂
q
∂
q
∂qE
1
2
3
e −1
e
E −1
−E ⋅ 
+

( E + 1) ⋅ α


E ⋅ q1c − q2c − q3c − … − qec−1 − qec − … − qEc −1 − qEc
+
( E + 1)


+



+ ( E − 1) ⋅ q1c − q2c − q3c − … − qec−1 − qec − … − qEc −1
qE =
1
( E + 1) ⋅ α

⋅  ( E + 1 − E ) ⋅ po −

(
)
− ( E − 1) ⋅ ( E + 1) − E 2 ⋅
+
1
( E + 1)
((
∂C1
∂C
+ ( E +1− E ) ⋅ 2 +
∂q1
∂q2
+ ( E +1− E ) ⋅
∂C3
∂C
+ … + ( E + 1 − E ) ⋅ e −1 +
∂q3
∂qe −1
+ ( E +1− E ) ⋅
∂Ce
∂C
∂C 
+ … + ( E + 1 − E ) ⋅ E −1 − E ⋅ E  +
∂qe
∂qE −1
∂qE 
)
⋅ − E 2 + ( E − 1) ⋅ ( E + 1) ⋅ q1c + ( E − ( E + 1) ) ⋅ q2c +
+ ( E − ( E + 1) ) ⋅ q3c + … + ( E − ( E + 1) ) ⋅ qec−1 +
+ ( E − ( E + 1) ) ⋅ qec + … + ( E − ( E + 1) ) ⋅ qEc −1 + E ⋅ qEc
qE =
1
( E + 1) ⋅ α
+
qE =
+

∂C ∂C
∂C
∂C
∂C
∂C
∂C
⋅  po + 1 + 2 + 3 + … + e −1 + e + … + E −1 − E ⋅ E
∂
q
∂
q
∂
q
∂
q
∂
q
∂
q
∂qE
1
2
3
e −1
e
E −1

(
1
⋅ −q1c − q2c − q3c − … − qec−1 − qec − … − qEc −1 + E ⋅ qEc
E
( + 1)
po +
)
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
∂C
+
+
+ … + e −1 + e + … + E −1 − E ⋅ E
∂q1 ∂q2 ∂q3
∂qe−1 ∂qe
∂qE −1
∂qE
+
( E + 1) ⋅ α
− q1c − q2c − q3c − … − qec−1 − qec − … − qEc −1 + E ⋅ qEc
( E + 1)
Sustituyendo ahora en la ecuación que define qe :
78
)

+

5.2 Formulación del modelo
qe =
po − ( e − 1) ⋅
∂C
∂C1 ∂C2 ∂C3
+
+
+ … + e −1
∂q1 ∂q2 ∂q3
∂qe −1
α
−
∂C1 ∂C2 ∂C3
∂Ce −1 ∂Ce
∂C
∂C

+
+ … + E −1 + E
 po − E ⋅ ∂q + ∂q + ∂q + … + ∂q
∂
q
∂
q
∂qE
1
2
3
e −1
e
E −1
−e ⋅ 
+

( E + 1) ⋅ α



E ⋅ q1c − q2c − q3c − … − qec−1 − qec − … − qEc −1 − qEc 
−
+

( E + 1)


∂
C
∂
C
∂
C
∂
C
∂C
∂C
∂
C
∂
C

e −1
3
1
2
+ e − E ⋅ e +1 + … + E −1 + E
 po + ∂q + ∂q + ∂q + … + ∂q
∂qe
∂qe +1
∂qE −1 ∂qE
1
2
3
e −1
+
−

( E + 1) ⋅ α



−q1c − q2c − q3c − … − qec−1 − qec + E ⋅ qec+1 − … − qEc −1 − qEc 
 −… −
+

( E + 1)


∂Ce −1 ∂Ce
∂C1 ∂C2 ∂C3
∂CE −1
∂C

+
+… +
−E⋅ E
 po + ∂q + ∂q + ∂q + … + ∂q
∂
q
∂
q
∂qE
1
2
3
e −1
e
E −1
−
+

( E + 1) ⋅ α



−q1c − q2c − q3c − … − qec−1 − qec − … − qEc −1 + E ⋅ qEc 
+
+

( E + 1)


+ ( e − 1) ⋅ q1c − q2c − q3c − … − qec−1
79
5 Generalización del modelo de Allaz y Vila
qe =
1
+
E
( 1) ⋅ α


⋅   ( E + 1) −
−… − 1 ⋅ po +
e −1



−E

+ ( − ( e − 1) ⋅ ( E + 1) + e ⋅ E − 1 − … − 1) ⋅
∂C1
+
∂q1

 ∂C 
 ∂C
+  ( E + 1) −
e −1
−… − 1 ⋅ 2 +  ( E + 1) −
e −1
−… − 1 ⋅ 3 + … +

 ∂q


2

−E


−E
 ∂q3

 ∂C

 ∂C
+  ( E + 1) −
−… − 1  ⋅ e −1 +  −
−… − 1 ⋅ e +
e −1
e −1

 ∂qe −1  

−E

−E

 ∂qe

 ∂C

 ∂C
+ E −
e −1
−… − 1  ⋅ e +1 + … +  E −
e −1
−… − 1 ⋅ E −1 +




− E +1
− E +1

 ∂qe+1

 ∂qE −1

 ∂C
e −1
+ E −
−… − 1 ⋅ E
 

− E +1
 ∂qE
+

+


(
1
⋅ ( −e ⋅ E + 1 + … + 1 + ( e − 1) ⋅ ( E + 1) ) ⋅ q1c +
E
1
+
(
)




+ 1 + … + 1 − ( E + 1)  ⋅ q3c + … +
+  e
+ 1 + … + 1 − ( E + 1)  ⋅ q2c +  e




E


E






+  e
+ 1 + … + 1 − ( E + 1)  ⋅ qec−1 +  e
+ 1 + … + 1 ⋅ qec +








E
E




+  − E + e
+ 1 + … + 1 ⋅ qec+1 + … +  − E + e
+ 1 + … + 1 ⋅ qEc −1 +








E −1
E −1



+  − E + e
+ 1 + … + 1 ⋅ qEc 




E −1


qe =
1
( E + 1) ⋅ α


 ∂C
⋅  po +  −e ⋅ E + E + 1 + e ⋅ E −
e −1
−… − 1 ⋅ 1 +



−E

 ∂q1

+
+
∂C
∂C
∂C2 ∂C3
∂C
∂C 
+
+ … + e −1 − E ⋅ e + … + E −1 + E  +
∂q2 ∂q3
∂qe −1
∂qe
∂qE −1 ∂qE 


1
1 +
⋅   −e ⋅ E +
…
+ 1 +e + e ⋅ E − E − 1 ⋅ q1c −



( E + 1)  
E


− q2c − q3c − … − qec−1 + E ⋅ qec − … − qEc −1 − qEc 

po +
qe =
+
80
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
∂C
+
+
+ … + e −1 − E ⋅ e + … + E −1 + E
∂q1 ∂q2 ∂q3
∂qe −1
∂qe
∂qE −1 ∂qE
+
( E + 1) ⋅ α
− q1c − q2c − q3c − … − qec−1 + E ⋅ qec − … − qEc −1 − qEc
( E + 1)
5.2 Formulación del modelo
Por tanto, la producción de cualquier empresa e se puede escribir como una función de las
producciones a plazo de todas las empresas dada por:
po − E ⋅
qe =
∂Ce
∂Cee
+ ∑
∂qe ee ≠ e ∂qee
( E + 1) ⋅ α
E ⋅ qec −
+
∑ qeec
ee ≠ e
( E + 1)
∀e
El precio de la energía, entonces, se puede escribir como:
∂C1 ∂C2
∂CE

 po − E ⋅ ∂q + ∂q + … + ∂q
E ⋅ q1c − q2c − … − qEc
1
2
E
p = po − α ⋅ 
+
+

( E + 1) ⋅ α
( E + 1)


∂C
∂C
∂C
po + 1 − E ⋅ 2 + … + E
∂q1
∂q2
∂qE −q1c + E ⋅ q2c − … − qEc
+
+
+…+
( E + 1) ⋅ α
( E + 1)
+
po +
∂C1 ∂C2
∂C
+
+…− E ⋅ E
∂q1 ∂q2
∂qE −q1c − q2c − … + E ⋅ qEc
+
( E + 1) ⋅ α
( E + 1)
∂C1 ∂C2
∂CE

 E ⋅ po − ∂q − ∂q − … − ∂q
q c + q2c + … + qEc
1
2
E
p = po − α ⋅ 
+ 1

( E + 1) ⋅ α
( E + 1)


p=
po +
∂C1 ∂C2
∂C
+
+ … + E α ⋅ qc + qc + … + qc
1
2
E
∂q1 ∂q2
∂qE
−
( E + 1)
( E + 1)
(












)
El precio del mercado es una función de las ventas a plazo de todas las empresas generadoras:
po + ∑
p=
5.2.2
e
∂Ce
∂qe
( E + 1)
α ⋅ ∑ qec
−
e
( E + 1)
Mercado a plazo
En la primera etapa los agentes deben elegir qué cantidad contratar a plazo para
maximizar el beneficio total, teniendo en cuenta que sus decisiones de contratación
afectarán tanto al precio del mercado como a las cantidades totales producidas:
(
)
max p c ⋅ qec + p s ⋅ qe − qec − Ce
∀e
(5.11)
81
5 Generalización del modelo de Allaz y Vila
y como p c = p s = p
max p ⋅ qe − Ce
∀e
(5.12)
El lagrangiano de cada empresa queda:
Le = p ⋅ qe − Ce
∀e
(5.13)
y las condiciones de optimalidad:
∂Le ∂p
∂q ∂C
= c ⋅ qe + p ⋅ ec − ce = 0
∂qe ∂qe
∂qe ∂qe
∀e
(5.14)
que, aplicando la regla de la cadena, se puede reescribir como:
∂p
∂qec
⋅ qe + p ⋅
∂qe
∂qec
−
∂Ce ∂qe
⋅
=0
∂qe ∂qec
∀e
(5.15)
De las expresiones que se han obtenido al resolver el problema de optimización de la
segunda etapa:
∂C
∂Cee

c
po − E ⋅ e + ∑
E ⋅ qec − ∑ qee

∂qe ee≠e ∂qee
ee ≠e
qe =
+
1
α
1)
E
+
⋅
E
+
(
)
(

 ∂q
E
 ec =
 ∂qe ( E + 1)
∂C

po + ∑ e α ⋅ ∑ qec

e qe
e
 p =
−
( E + 1)
( E + 1)

 ∂p
α
 c =−
( E + 1)
 ∂qe
Sustituyendo,
82
∀e
(5.16)
(5.17)
5.2 Formulación del modelo
∂Ce
∂Cee

c 
E ⋅ qec − ∑ qee
 po − E ⋅ ∂q + ∑ ∂q

α
e
ee
ee ≠ e
ee≠ e


−
⋅
+
+
( E + 1) 
( E + 1) ⋅α
( E + 1) 




∂Ce


α ⋅ ∑ qec 
 po + ∑ ∂q
E
e
e
e
−
+
⋅
−
( E + 1)  ( E + 1)
( E + 1) 




∂C
E
−
⋅ e =0
( E + 1) ∂qe
∀e
(5.18)
∀e
(5.19)
Resultado 5.2.B
Las condiciones de optimalidad de las empresas están dadas por:
po − E ⋅
 2E
∂Ce
∂Cee
c 
+∑
− α ⋅ 
⋅ qec + ∑ qee
 = 0
E
∂qe ee ≠e ∂qee
−
1
(
)
ee≠ e


Entonces, se puede plantear un sistema de E ecuaciones –las E ecuaciones de
optimalidad de las empresas– con E incógnitas –las cantidades contratadas a plazo por
cada empresa–.
83
5 Generalización del modelo de Allaz y Vila
∂Ce −1 ∂Ce
∂C1 ∂C2 ∂C3
∂C
∂C

+
+ … + E −1 + E −
 po − E ⋅ ∂q + ∂q + ∂q + … + ∂q
∂qe
∂qE −1 ∂qE
1
2
3
e −1


 2E

−α ⋅ 
⋅ q1c + q2c + q3c + … + qec−1 + qec + … + qEc −1 + qEc  = 0


 ( E − 1)


 po + ∂C1 − E ⋅ ∂C2 + ∂C3 + … + ∂Ce −1 + ∂Ce + … + ∂CE −1 + ∂CE −

∂q1
∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE

 c
2E

c
c
c
c
c
c 
α
q
q
−
⋅
+
⋅
+
q
+
…
+
q
+
q
+
…
+
q
+
q

 = 0
2
3
e
1
e
E
1
E
1
−
−


E
−
1
(
)




∂C3
∂Ce −1 ∂Ce
∂C1 ∂C2
∂CE −1 ∂CE
+
−E⋅
+… +
+
+… +
+
−
 po +
∂q1 ∂q2
∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE




2E

−α ⋅  q1c + q2c +
⋅ q3c + … + qec−1 + qec + … + qEc −1 + qEc  = 0



( E − 1)



⋮

∂C
∂C
∂C
∂C ∂C
∂C
∂C
 po + 1 + 2 + 3 + … − E ⋅ e −1 + e + … + E −1 + E −
∂qE −1 ∂qE
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe




2E

−α ⋅  q1c + q2c + q3c + … +
⋅ qec−1 + qec + … + qEc −1 + qEc  = 0

( E − 1)



∂Ce −1
∂C
∂C1 ∂C2 ∂C3
∂C
∂C

− E ⋅ e + … + E −1 + E −
 po + ∂q + ∂q + ∂q + … + ∂q
∂qe
∂qE −1 ∂qE
1
2
3
e −1




2E
−α ⋅  q1c + q2c + q3c + … + qec−1 +
⋅ qec + … + qEc −1 + qEc  = 0

( E − 1)




⋮

∂C
∂C
∂C1 ∂C2 ∂C3
∂C
∂C
+
+
+ … + e −1 + e + … − E ⋅ E −1 + E −
 po +
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE




2E

−α ⋅  q1c + q2c + q3c + … + qec−1 + qec + … +
⋅ qEc −1 + qEc  = 0

( E − 1)



 p + ∂C1 + ∂C2 + ∂C3 + … + ∂Ce −1 + ∂Ce + … + ∂CE −1 − E ⋅ ∂CE −
 o ∂q
∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1
∂qE
1




2E
−α ⋅  q1c + q2c + q3c + … + qec−1 + qec + … + qEc −1 +
qEc  = 0
⋅


( E − 1) 


(5.20)
Resultado 5.2.C
En el equilibrio, las cantidades que cada empresa contrata a plazo son:
84
5.2 Formulación del modelo
qec
(
)


E 3 + 1 ∂C
∂Cee 

=
⋅ po −
⋅ e +E⋅ ∑

( E + 1) ∂qe
E 2 + 1 ⋅α 
ee ≠ e ∂qee


(
( E − 1)
)
∀e
(5.21)
Se puede comprobar fácilmente que en el caso en el que
• hay dos empresas ( E = 2 )
• los costes de producción de las empresas son una función lineal de la producción
( Ce = c ⋅ qe )
• la pendiente de la ecuación del precio es 1 (α = 1)
la ecuación (5.21) da los mismos resultados que se obtuvieron en el apartado 4.2.
Demostración 5.2.B
∂Ce
∂Cee

c
E ⋅ qec − ∑ qee
 po − E ⋅ ∂q + ∑ ∂q
e
ee
ee ≠ e
ee ≠ e
−
⋅
+
( E + 1) 
( E + 1) ⋅ α
( E + 1)


∂Ce


α ⋅ ∑ qec 
 po + ∑ ∂q
E
e
e
e
−
+
⋅
−
( E + 1)  ( E + 1)
( E + 1) 




∂C
E
−
⋅ e =0
( E + 1) ∂qe
α
− po + E ⋅


+




∂Ce
∂Cee
c 
−∑
− α ⋅  E ⋅ qec − ∑ qee
 +
∂qe ee ≠ e ∂qee
ee ≠ e


+ E ⋅ po + E ⋅

∂Ce
∂Cee
c 
+E⋅ ∑
− α ⋅  E ⋅ qec + E ⋅ ∑ qee
 −
∂qe
ee ≠ e ∂qee
ee ≠ e


− E ⋅ ( E + 1) ⋅
∂Ce
=0
∂qe
( E − 1) ⋅ po + ( 2 E − E ⋅ ( E + 1) ) ⋅
∂Ce
∂Cee
+ ( E − 1) ⋅ ∑
−
∂qe
ee ≠ e ∂qee

c 
−α ⋅  2 E ⋅ qec + ( E − 1) ⋅ ∑ qee
 = 0

ee ≠ e

Por tanto, las condiciones de optimalidad de las empresas se pueden expresar como:
po − E ⋅
 2E
∂Ce
∂Cee
c 
+ ∑
−α ⋅
⋅ qec + ∑ qee
 = 0

∂qe ee ≠ e ∂qee
ee ≠ e
 ( E − 1)

85
5 Generalización del modelo de Allaz y Vila
Demostración 5.2.C

 po





p
 o





 po





⋮

p
 o






 po





⋮

 po






 po




−E⋅
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
∂C
+
+
+ … + e −1 + e + … + E −1 + E −
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE
 2E

−α ⋅ 
⋅ q1c + q2c + q3c + … + qec−1 + qec + … + qEc −1 + qEc  = 0
 ( E − 1)

∂C1
∂C2 ∂C3
∂Ce −1 ∂Ce
∂CE −1 ∂CE
+
−E⋅
+
+… +
+
+…+
+
−
∂q1
∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE


2E
−α ⋅  q1c +
⋅ q2c + q3c + … + qec−1 + qec + … + qEc −1 + qEc  = 0


( E − 1)


∂C ∂C
∂C
∂C
∂C
∂C
∂C
+ 1 + 2 − E ⋅ 3 + … + e −1 + e + … + E −1 + E −
∂q1 ∂q2
∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE


2E
−α ⋅  q1c + q2c +
⋅ q3c + … + qec−1 + qec + … + qEc −1 + qEc  = 0
( E − 1)


+
∂C
∂C
∂C
∂C
∂C1 ∂C2 ∂C3
+
+
+ … − E ⋅ e −1 + e + … + E −1 + E −
∂qE −1 ∂qE
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe


2E
−α ⋅  q1c + q2c + q3c + … +
⋅ qec−1 + qec + … + qEc −1 + qEc  = 0
( E − 1)


∂C
∂C
∂C
∂C ∂C
∂C
∂C
+ 1 + 2 + 3 + … + e −1 − E ⋅ e + … + E −1 + E −
∂q1 ∂q2 ∂q3
∂qe −1
∂qe
∂qE −1 ∂qE


2E
−α ⋅  q1c + q2c + q3c + … + qec−1 +
⋅ qec + … + qEc −1 + qEc  = 0
( E − 1)


+
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
∂C
+
+
+ … + e −1 + e + … − E ⋅ E −1 + E −
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE


2E
−α ⋅  q1c + q2c + q3c + … + qec−1 + qec + … +
⋅ qEc −1 + qEc  = 0
E
−
1
(
)


∂Ce −1 ∂Ce
∂C1 ∂C2 ∂C3
∂CE −1
∂CE
+
+
+
+… +
+
+… +
−E⋅
−
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1
∂qE


2E
⋅ qEc  = 0
−α ⋅  q1c + q2c + q3c + … + qec−1 + qec + … + qEc −1 +
−
E
1
(
)


c
Despejando q2 de la primera ecuación del sistema anterior:
po − E ⋅
q2c =
α
−
86
∂C1 ∂C2 ∂C3
∂C
∂C
∂C
∂C
+
+
+ … + e −1 + e + … + E −1 + E
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE
2E
( E − 1)
⋅ q1c − q3c − … − qec−1 − qec − … − qEc −1 − qEc
−
5.2 Formulación del modelo
Sustituyendo esta expresión en la ecuación E del sistema:
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
∂C
+
+
+ … + e −1 + e + … + E −1 − E ⋅ E −
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1
∂qE
po +
∂C
∂C
∂C
∂C ∂C
∂C
∂C

po − E ⋅ 1 + 2 + 3 + … + e −1 + e + … + E −1 + E

∂
q
∂
q
∂
q
∂
q
∂
q
∂
q
∂qE
1
2
3
e −1
e
E −1
−α ⋅  q1c +
−
α



2E
−
⋅ q c − q c − … − qec−1 − qec − … − qEc −1 − qEc +
( E − 1) 1 3


2
E
+ q3c + … + qec−1 + qec + … + qEc −1 +
⋅ qEc  = 0
( E − 1) 


( E + 1) ⋅
 ( E + 1) c ( E + 1) c 
∂C1
∂C
− ( E + 1) ⋅ E − α ⋅  −
⋅ q1 +
⋅q  = 0
∂q1
∂qE
( E − 1) E 
 ( E − 1)
∂C1 ∂CE
α
−
−
⋅ − q1c + qEc = 0
∂q1 ∂qE ( E − 1)
(
)
 ∂C1 ∂CE 
−

 ∂q1 ∂qE  + q c
( E − 1) ⋅ 
qEc =
α
1
Se sustituye ahora q2c en la ecuación E-1 del sistema:
po +
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
∂C
+
+
+ … + e −1 + e + … − E ⋅ E −1 + E −
∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE
∂C ∂C
∂C
∂C
∂C
∂C
∂C

po − E ⋅ 1 + 2 + 3 + … + e −1 + e + … + E −1 + E

∂
q
∂
q
∂
q
∂
q
∂
q
∂
q
∂qE
1
2
3
e −1
e
E −1
−α ⋅  q1c +
−
α



2E
−
⋅ q c − q c − … − qec−1 − qec − … − qEc −1 − qEc +
( E − 1) 1 3
+ q3c
( E + 1) ⋅
+ … + qec−1
+ qec


2E
c
c 
+…+
⋅ q E −1 + q E = 0

( E − 1)


 ( E + 1) c ( E + 1) c 
∂C1
∂C
− ( E + 1) ⋅ E −1 − α ⋅  −
⋅ q1 +
⋅q
=0
∂q1
∂qE −1
( E − 1) E −1 
 ( E − 1)
∂C1 ∂CE −1
α
−
−
⋅ −q1c + qEc −1 = 0
∂q1 ∂qE −1 ( E − 1)
(
)
87
5 Generalización del modelo de Allaz y Vila
 ∂C1 ∂CE −1 
−

 ∂q1 ∂qE −1 
( E − 1) ⋅ 
qEc −1 =
α
+ q1c
Se sustituye q2c progresivamente en las distintas ecuaciones del sistema. Al llegar a la ecuación e
se tiene:
po +
∂C
∂C
∂C1 ∂C2 ∂C3
∂C
∂C
+
+
+ … + e −1 − E ⋅ e + … + E −1 + E −
∂q1 ∂q2 ∂q3
∂qe −1
∂qe
∂qE −1 ∂qE
∂C
∂C
∂C
∂C ∂C
∂C
∂C

po − E ⋅ 1 + 2 + 3 + … + e −1 + e + … + E −1 + E

∂q1 ∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE
−α ⋅  q1c +
−
α



2E
−
⋅ q1c − q3c − … − qec−1 − qec − … − qEc −1 − qEc +
E
−
1
(
)
+ q3c
( E + 1) ⋅
+ … + qec−1


2E
c
c
c 
+
⋅ qe + … + qE −1 + qE = 0

( E − 1)


 ( E + 1) c ( E + 1) c 
∂C1
∂C
− ( E + 1) ⋅ e − α ⋅  −
⋅ q1 +
⋅q  = 0
∂q1
∂qe
( E − 1) e 
 ( E − 1)
∂C1 ∂Ce
α
−
−
⋅ − q1c + qec = 0
∂q1 ∂qe ( E − 1)
(
)
 ∂C1 ∂Ce 
−

 ∂q1 ∂qe  + q c
( E − 1) ⋅ 
qec =
α
1
Se repite el proceso hasta que, finalmente, se sustituye q2c en la segunda ecuación del sistema:
po +
∂C
∂C
∂C
∂C1
∂C
∂C
∂C
− E ⋅ 2 + 3 + … + e −1 + e + … + E −1 + E −
∂q1
∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE

∂Ce −1 ∂Ce
∂C1 ∂C2 ∂C3
∂C
∂C

+
+ … + E −1 + E

 po − E ⋅ ∂q + ∂q + ∂q + … + ∂q
∂
q
∂
q
∂qE
2
E
1
2
3
e −1
e
E −1
−α ⋅  q1c +
⋅
−

E
−
1
α

(
)






2E
c
c
c
c
c
c 
−
⋅ q1 − q3 − … − qe−1 − qe − … − qE −1 − qE +

( E − 1)




+ q3c + … + qec−1 + qec + … + qEc −1 + qEc  = 0



88
5.2 Formulación del modelo
2 E 2 + ( E − 1) ∂C1 E ⋅ ( E + 1) ∂C2 ( E + 1) ∂C3
( E + 1)
⋅ po +
⋅
−
⋅
−
⋅
−… −
∂q1
( E − 1)
( E − 1)
( E − 1) ∂q2 ( E − 1) ∂q3
( E + 1) ∂Ce−1 ( E + 1) ∂Ce
( E + 1) ∂CE −1 ( E + 1) ∂CE
−
⋅
−
⋅
−… −
⋅
−
⋅
−
( E − 1) ∂qe−1 ( E − 1) ∂qe
( E − 1) ∂qE −1 ( E − 1) ∂qE
−
 ( E − 1)2 − 4 E 2
( E + 1) c
( E + 1) c ( E + 1) c
−α ⋅ 
⋅ q1c −
⋅ q3 − … −
⋅q −
⋅ q −… −
2

( E − 1)
( E − 1) e−1 ( E − 1) e
( E − 1)

−
− po +
( E + 1)
( E − 1)
⋅ qEc −1 −
( E + 1) c 
⋅q = 0
( E − 1) E 
2 E 2 + ( E − 1) ∂C1
∂C
∂C
∂C
∂C
∂C
∂C
⋅
− E ⋅ 2 − 3 − … − e −1 − e − … − E −1 − E −
∂q1
∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE
( E + 1)
 ( E − 1) 2 − 4 E 2

−α ⋅ 
⋅ q1c − q3c − … − qec−1 − qec − … − qEc −1 − qEc  = 0
 E − 1) ⋅ ( E + 1)

(

Sustituyendo todas las expresiones obtenidas anteriormente:
− po +
2 E 2 + ( E − 1) ∂C1
∂C
∂C
∂C
∂C
∂C
∂C
⋅
− E ⋅ 2 − 3 − … − e −1 − e − … − E −1 − E −
∂q1
∂q2 ∂q3
∂qe −1 ∂qe
∂qE −1 ∂qE
( E + 1)
 ( E − 1) 2 − 4 E 2
( E − 1)  ∂C1 ∂C3  c
−α ⋅ 
⋅ qc −
⋅
−
 − q1 − … −
 ( E − 1) ⋅ ( E + 1) 1
α
∂q1 ∂q3 


( E − 1)  ∂C1 ∂Ce−1  c ( E − 1)  ∂C1 ∂Ce  c
−
⋅
−
⋅
−
 − q1 −
 − q1 − … −
α
α
 ∂q1 ∂qe −1 
 ∂q1 ∂qe 
−
( E − 1)
α
 ∂C ∂C

( E − 1)  ∂C1 ∂CE  c 
⋅  1 − E −1  − q1c −
⋅
−
 − q1 
α
 ∂q1 ∂qE −1 
 ∂q1 ∂qE 

 2 E 2 + ( E − 1)
 ∂C
∂C
∂C
− po + 
+ ( E − 2 ) ⋅ ( E − 1)  ⋅ 1 − E ⋅ 2 − (1 + ( E − 1) ) ⋅ 3 − … −


∂q2
∂q3
( E + 1)

 ∂q1
∂C
∂C
− (1 + ( E − 1) ) ⋅ e −1 − (1 + ( E − 1) ) ⋅ e − … −
∂qe−1
∂qe
− (1 + ( E − 1) ) ⋅
∂CE −1
∂C
− (1 + ( E − 1) ) ⋅ E −
∂qE −1
∂qE
  ( E − 1)2 − 4 E 2


−α ⋅  
− ( E − 2 )  ⋅ q1c  = 0

  ( E − 1) ⋅ ( E + 1)




89
5 Generalización del modelo de Allaz y Vila
(
)
 2 E 2 + ( E − 1) + E 3 − 2 E 2 − E + 2 
 ⋅ ∂C1 −
− po + 

 ∂q1
( E + 1)


∂C
∂C
∂C
∂C
∂C
∂C
− E ⋅ 2 − E ⋅ 3 − … − E ⋅ e −1 − E ⋅ e − … − E ⋅ E −1 − E ⋅ E −
∂q2
∂q3
∂qe −1
∂qe
∂qE −1
∂qE
(
)  ⋅ qc  = 0
  E 2 − 2E + 1 − 4 E 2 − E 3 − 2 E 2 − E + 1

−α ⋅  
( E − 1) ⋅ ( E + 1)
 

− po +
−E ⋅


1



( E 3 + 1) ⋅ ∂C1 − E ⋅ ∂C2 − E ⋅ ∂C3 − … −
( E + 1)
∂q1
∂q2
∂q3
∂Ce −1
∂C
∂C
∂C
− E ⋅ e − … − E ⋅ E −1 − E ⋅ E −
∂qe −1
∂qe
∂qE −1
∂qE
(
)
 −E3 − E 2 − E −1

−α ⋅ 
⋅ q1c  = 0
 ( E − 1) ⋅ ( E + 1)



− po +
−E ⋅
( E 3 + 1) ⋅ ∂C1 − E ⋅ ∂C2 − E ⋅ ∂C3 − … −
( E + 1)
∂q1
∂q2
∂q3
∂Ce −1
∂C
∂C
∂C
− E ⋅ e − … − E ⋅ E −1 − E ⋅ E −
∂qe −1
∂qe
∂qE −1
∂qE
(
) (
)
 −E ⋅ E 2 + 1 − E2 +1

−α ⋅ 
⋅ q1c  = 0


( E − 1) ⋅ ( E + 1)


− po
E 3 + 1) ∂C
(
∂C
∂C
+
⋅ 1 − E ⋅ 2 − E ⋅ 3 −… −
( E + 1)
∂q1
∂q2
∂q3
∂C
∂C
∂C
∂C
− E ⋅ e −1 − E ⋅ e − … − E ⋅ E −1 − E ⋅ E −
∂qe −1
∂qe
∂qE −1
∂qE
(
)
 − E2 +1

−α ⋅ 
⋅ q1c  = 0
 ( E − 1)



q1c
(
(
)
( ) + E ⋅ ∂Ce−1 − E ⋅ ∂Ce − … − E ⋅ ∂CE −1 − E ⋅ ∂CE 
( )
90
)

E 3 + 1 ∂C
∂C
∂C

=
⋅ po −
⋅ 1 + E ⋅ 2 + E ⋅ 3 +… +
2

∂q2
∂q3
( E + 1) ∂q1
E + 1 ⋅α 

( E − 1)
∂qe −1
∂qe
∂qE −1
∂qE 

5.3 Análisis de los resultados
Sustituyendo esta última expresión en la ecuación obtenida para qec :
qec =
( E − 1)
α
+
(
 ∂C ∂C 
⋅ 1 − e  +
 ∂q1 ∂qe 
(
)
( ) + E ⋅ ∂Ce−1 − E ⋅ ∂Ce − … − E ⋅ ∂CE −1 − E ⋅ ∂CE 
( )
qec =
(
)

E 3 + 1 ∂C
∂C
∂C
⋅  po −
⋅ 1 + E ⋅ 2 + E ⋅ 3 +…+
2

∂q2
∂q3
( E + 1) ∂q1
E + 1 ⋅α 

( E − 1)
∂qe −1
∂qe
∂qE −1
(
∂qE 

)

E 3 + E 2 + E + 1 − E 3 − 1 ∂C
∂C
∂C
⋅  po +
⋅ 1 + E ⋅ 2 + E ⋅ 3 +… +
2

E
1
q
q
+
∂
∂
∂q3
(
)
E + 1 ⋅α 
1
2

( E − 1)
)
(
)
− E 2 − 1 + E ⋅ ( E + 1) ∂C
∂Ce −1
∂C
∂C
+E ⋅
−
⋅ e − … − E ⋅ E −1 − E ⋅ E
E
1
q
q
∂qe−1
+
∂
∂
∂qE
(
)
e
E −1
qec =
(
( E − 1)

∂C
∂C
∂C
⋅  po + E ⋅ 1 + E ⋅ 2 + E ⋅ 3 + … +
∂q1
∂q2
∂q3
E + 1 ⋅α 
2
)
+E ⋅
(
)
E 3 + 1 ∂C
∂Ce −1
∂C
∂C
−
⋅ e − … − E ⋅ E −1 − E ⋅ E
∂qe−1 ( E + 1) ∂qe
∂qE −1
∂qE




Por tanto, en el equilibrio, la producción a plazo de las empresas está dada por:
qec
(
)

E 3 + 1 ∂C
∂Cee

=
⋅ po −
⋅ e +E⋅ ∑
2

( E + 1) ∂qe
E + 1 ⋅α 
ee ≠ e ∂qee

(
( E − 1)
)




∀e
5.3 Análisis de los resultados
La generalización del modelo de Allaz y Vila no altera ninguno de los resultados
obtenidos para el caso particular presentado en el capítulo 4. Como en el caso anterior,
el modelo –que no es más que una generalización del desarrollado por Allaz y Vila–
revela un efecto procompetitivo de los mercados a plazo5. Sin embargo, haber obtenido
unas expresiones generales permite no sólo aplicar el modelo a un caso más realista y
estudiar sus resultados en el contexto de alguno de los mercados eléctricos existentes,
5
Para más detalles, véase capítulo 4.
91




5 Generalización del modelo de Allaz y Vila
sino también analizar con mayor detalle la influencia de los mercados a plazo en el
comportamiento de los agentes cuando operan en un mercado spot.
Considérese una cierta empresa e que decide contratar un megavatio-hora adicional en
el mercado a plazo. Según su condición de optimalidad (ecuación (5.7)):
(
)
p − α ⋅ qe − qec −
∂Ce
=0
∂qe
⇒
∆qe = ∆qec
La empresa e decidiría entonces aumentar un megavatio-hora su producción total. En
efecto, al aumentar la cantidad contratada disminuye la producción de la empresa
sensible al precio del spot, ya que una reducción del mismo no afecta a los contratos
negociados en la etapa anterior. Se puede decir que la potencia inframarginal de la
empresa se reduce y, por tanto, disminuyen los incentivos para retirar cantidad del
mercado y mantener los precios altos. En consecuencia, la empresa encuentra que
aumentando su producción total aumentan sus beneficios porque la bajada del precio
que conlleva el incremento de producción no tiene efecto sobre el megavatio-hora
adicional contratado, cuya remuneración ya es fija.
En principio, el aumento de producción de la empresa e haría que el precio de mercado
bajase una cantidad –α, suponiendo que ninguna empresa reacciona ante la variación
de generación y es la demanda la que absorbe el incremento de producción:
p = po − α ⋅ ∑ qe
⇒
∆p = −α
e
Sin embargo, el incremento de producción de la empresa e no es una decisión
independiente, sino que se trata de una variación asociada al aumento de su
contratación. Por tanto, la información es pública para todos los agentes, que pueden
prever el aumento de generación en el spot y reaccionar modificando sus producciones
en este mercado. En otras palabras, la empresa e indica a todos los agentes su intención
de aumentar su generación en el spot mediante el incremento de su cantidad
contratada, de modo que todos los agentes, incluida la propia empresa e, pueden
modificar sus producciones para adaptarse al nuevo nivel de precio.
El efecto de estas reacciones se recoge en la demanda residual de los contratos de la
empresa e. La demanda residual es una función que relaciona el precio de mercado de
la energía eléctrica con la generación de cada empresa, teniendo en cuenta tanto la
demanda de energía de los consumidores como las actuaciones de las empresas en el
mercado. La curva de demanda residual de los contratos de la empresa e se define
como la diferencia entre la demanda total y la cantidad que ofertan a determinado
precio todos los agentes del spot, ya que todos ellos reaccionan ante los cambios en los
contratos de una empresa. Esta curva relaciona de forma directa el precio de la energía
con la cantidad que contrata a plazo la empresa e, considerando al mismo tiempo las
influencias de las reacciones de las empresas en el spot como las de la demanda de
energía.
92
5.3 Análisis de los resultados
Por tanto, la derivada del precio respecto de la contratación de una empresa puede
expresarse en función de un único parámetro: la pendiente de la demanda residual. De
acuerdo con la ecuación (5.17), esta pendiente tendrá valor:
∂p
∂qec
=−
α
(5.22)
( E + 1)
En efecto, según (5.1) y (5.7):
p = po − α ⋅ D
(
∂D
1
=−
α
∂p
⇒
)
p − α ⋅ qe − qec −
∂Ce
=0
∂qe
(5.23)
∂qe 1
=
∂p α
⇒
∀e
(5.24)
La pendiente de la demanda residual de los contratos de una empresa, teniendo en
cuenta que una variación de los contratos influye tanto en la demanda total de energía
como en todas las empresas del spot, será:
∂p
∂qec
=
1
−
1
α
−E⋅
1
=−
α
α
(5.25)
E +1
Así que un aumento unitario de la cantidad contratada por la empresa e provoca una
reducción del precio igual a −
α
E +1
. Nótese que cuanto mayor es el número de
empresas que compiten en el spot, menor es la variación que experimenta el precio, ya
que cambios en los contratos de una empresa se ven amortiguados por un mayor
número de agentes, que contrarrestan sus efectos.
Las relaciones anteriores se representan gráficamente en la siguiente figura:
q
∆qe
C
qe
B
A
∆qe
c
Demanda residual
p
Figura 5.1: Efecto del incremento de la producción a plazo de una empresa
93
5 Generalización del modelo de Allaz y Vila
El punto A representa el equilibrio inicial del mercado, dado por el punto de corte de la
curva de demanda residual y la producción de la empresa e. Si ahora la empresa e
decide aumentar la cantidad contratada en una cantidad ∆qec , su producción total
también crecerá en una cantidad igual al incremento del volumen de contratos ∆qec , y
el precio sufrirá una cierta reducción. El punto B representa el precio que resultaría si
las empresas del spot no reaccionasen ante los cambios en la producción a plazo de la
empresa e. Sin embargo, estas variaciones en la cantidad de contratos sí son conocidas
por los agentes, que reducen su producción y compensan, en parte, la bajada de precio
anterior. De modo que el precio de mercado está representado por el punto C, definido
por el punto de corte de la curva de demanda residual de los contratos de la empresa e
y la nueva producción de esta empresa debido al incremento en su contratación.
Entonces, la bajada que experimenta el precio cuando una empresa aumenta la
cantidad vendida a plazo hace que los agentes disminuyan su producción total:
(
)
p − α ⋅ qe − qec −
∂Ce
=0
∂qe
⇒
∆qe = −
1
( E + 1)
∀e
(5.26)
Es decir, cuando la empresa e incrementa unitariamente su cantidad de contratos a
plazo, todas las empresas disminuyen su producción total en −
1
. Este efecto se
( E + 1)
superpone, para el caso de la empresa e, al aumento de producción que se ha
comentado inicialmente, asociado a la reducción de producción sensible al precio del
spot. Por tanto, la derivada de la producción de la empresa e respecto de sus propios
contratos tiene dos términos:
• el aumento de producción debido a la disminución de su potencia inframarginal
en el spot
• la reducción de producción como reacción a la bajada de precio spot que implica
el aumento anterior, y que puede ser previsto por los agentes ya que conocen las
cantidades negociadas en el mercado a plazo
∂qe
∂qec
= 1−
1
E
=
( E + 1) ( E + 1)
(5.27)
En efecto, de la ecuación (5.9) que define la producción total de las empresas en
función de las ventas a plazo de todos los agentes se tiene que:
E
 ∂qe
 c = ( E + 1)
 ∂qe

 ∂qe = − 1
c
 ∂qee
( E + 1)
(5.28)
Por tanto, un aumento en las ventas a plazo de una empresa hace que esa empresa esté
menos expuesta al precio spot. La nueva cantidad óptima que debe producir aumenta,
94
5.4 El coste de producción
provocando con ello una reducción del precio del mercado spot. La cantidad contratada
a plazo por la empresa es conocida por todos los agentes, que modifican sus
producciones para adaptarse a las decisiones de la primera etapa. Así, todos los
agentes, incluida la propia empresa e, reaccionan reduciendo su producción en el
mercado de corto plazo para compensar, en parte, el aumento de producción y
amortiguar la bajada de precio.
5.4 El coste de producción
El modelo de Allaz y Vila representa los costes de producción de las empresas como
funciones lineales de la producción total de las mismas. Sin embargo, típicamente, cada
empresa tiene varios generadores de su propiedad con los que produce la cantidad
total que vende en el mercado. Cada generador tendrá, en general, diferentes costes de
producción.
En los modelos de largo plazo se suele aceptar que los costes de acoplamiento,
arranque y parada son despreciables cuando se considera un horizonte suficientemente
amplio. En estas condiciones, es necesario suponer que el mínimo técnico de los grupos
es igual a cero para permitir que existan generadores que no producen energía, ya que
el modelo no contiene variables que representen el estado de acoplamiento a la red de
las centrales eléctricas.
De modo que una representación razonable de los costes de producción de los
generadores consiste en suponer que el único coste relevante es el coste variable de
producción. Entonces, siguiendo lo descrito en el capítulo 3, el coste de producción de
un generador i está dado por una recta como la que se recoge en la Figura 5.2.
Ci
ci
gi
gi
Figura 5.2: Coste de producción del generador i
Por tanto, una representación más realista de los costes de producción de una empresa
se muestra en la Figura 5.3
95
5 Generalización del modelo de Allaz y Vila
Ce
Grupo 4
Grupo 3
Grupo 1
Grupo 2
qe
Figura 5.3: Coste de producción de la empresa e
Se trata de una función lineal a tramos. La empresa comenzará produciendo con el
generador de menor coste, y lo hará hasta que el grupo alcance su límite máximo de
producción y agote su capacidad de generación. Si la empresa desea seguir
produciendo, tendrá que recurrir a otro grupo y, para ello, escogerá el de menor coste
de entre los generadores no acoplados. Este grupo tendrá un coste variable de
producción diferente, lo que cambiará la pendiente de la curva de coste de la empresa.
A medida que el agente incrementa su producción debe utilizar generadores de mayor
coste según los grupos más baratos van alcanzando su potencia máxima, haciendo que
la pendiente de la curva aumente con cada nuevo generador empleado.
La derivada de la curva de costes de una empresa será, entonces, una escalera en la que
cada tramo es el coste de combustible de cada grupo entre su potencia mínima y su
potencia máxima.
∂C e
Grupo 4
∂qe
Grupo 3
Grupo 2
Grupo 1
qe
Figura 5.4: Derivada del coste de producción de la empresa e
Cuando un generador alcanza su potencia máxima y no puede seguir produciendo a
pesar de que el precio del mercado es suficiente para continuar generando, se activa la
restricción de potencia máxima del grupo y la variable dual µi
g
asociada a esta
restricción toma valor distinto de cero, tal y como se ha descrito en el capítulo 3.
Análogamente, si un grupo se ve forzado a producir una potencia mínima, la variable
96
5.5 Formulación general del modelo como un problema de equilibrio con restricciones de equilibrio
g
dual µi
tomará un cierto valor, que representa el incremento que se tendría en la
función objetivo si se relajase unitariamente esta restricción.
5.5 Formulación general del modelo como un problema
de equilibrio con restricciones de equilibrio
La formulación del modelo de Allaz y Vila es la de un problema de equilibrio con
restricciones de equilibrio (EPEC). Cuando un problema consta de varias etapas que
suceden de manera secuencial, las decisiones de unas etapas sirven como datos de
entrada para las otras. En el caso particular del modelo de Allaz y Vila, las reacciones
de los agentes en el mercado spot se incorporan al proceso de decisión en el mercado a
plazo, que depende, por tanto, del comportamiento que tendrán las empresas en la
siguiente etapa.
El problema de optimización de cada una de las empresas puede formularse de
manera general como un problema de optimización cuya función objetivo coincide con
la de la primera etapa, y que incorpora todas las condiciones de optimalidad del
problema del mercado spot como restricciones del problema:
(
)
∀e
∂Cee
=0
∂qee
∀ee
max p c ⋅ qec + p s ⋅ qe − qec − Ce
(
)
c
s.a. p s − α ⋅ qee − qee
−
(5.29)
donde
p s = pos − α s ⋅ ∑ qe es el precio del mercado spot,
e
p =
c
poc
− α ⋅ ∑ qec es el precio del mercado a plazo.
c
e
En este caso, el problema de cada empresa en el mercado a plazo considera
explícitamente todas las condiciones de optimalidad de todas las empresas. En el
planteamiento del apartado 5.2, estas condiciones se incluían en el problema de la
primera etapa a través de las expresiones calculadas para la producción de cada
empresa y el precio del mercado, que definían el equilibrio del spot. Aquí, sin embargo,
son las ecuaciones que definen el comportamiento óptimo de las empresas en la
segunda etapa las que aparecen como restricciones del problema.
5.6 Conclusiones
Los resultados del modelo de Allaz y Vila revelan que la existencia de mercados a
plazo hace que los agentes se comportan de forma más competitiva en el mercado spot.
Cuando una empresa se encuentra decidiendo su producción en el mercado de corto
97
5 Generalización del modelo de Allaz y Vila
plazo debe tener en cuenta que el volumen de energía que ya ha sido contratado recibe
el precio fijado en la primera etapa, de modo que las variaciones en el precio spot no
afectan a los ingresos de esa generación. Así, si una empresa decide aumentar la
cantidad de sus contratos en ∆qec , su potencia inframarginal sensible a una bajada del
precio spot se reduce en ∆qec . Por tanto, un mayor volumen de contratos a plazo hace
que la empresa incremente su producción total y, con ello, que el precio del mercado
baje.
Las decisiones de cada agente en el mercado a plazo son conocidas por todas las
empresas, de modo que éstas pueden anticipar el efecto de la contratación a plazo en el
equilibrio del mercado spot y adaptar sus producciones totales a las cantidades que
previamente se han comprometido en la primera etapa. La generalización del modelo
que se ha presentado en este capítulo permite analizar las reacciones de los agentes
ante una variación en la producción a plazo de una cierta empresa.
Cuando una empresa modifica su contratación en el mercado a plazo, todos los agentes
del spot prevén la variación en la producción de esta empresa y su influencia en el
precio de corto plazo. Por tanto, es esperable que todas las empresas que se verán
afectadas por los cambios en el precio spot reaccionen de alguna manera, cambiando su
producción en ∆qe , para amortiguar el efecto de estas variaciones. Así, si una empresa
e aumenta 1 MWh su generación en el mercado a plazo, su ingreso marginal en el
mercado spot aumenta y su decisión óptima será incrementar 1 MWh su producción
total. El precio spot sufrirá, por tanto, una reducción que afectará a la producción no
contratada de todas las empresas que operan en el mercado spot, de modo que todos
los agentes, incluida la propia empresa e, reaccionan reduciendo su producción para
adaptarse al nuevo nivel de precio y compensar, en parte, el incremento de producción
inicial. La reacción de la empresa e en el mercado spot tiene, entonces, dos términos:
• un aumento de producción asociado a la reducción de su potencia inframarginal
• una reducción de producción, igual a la reacción del resto de competidores,
asociada a la bajada de precio que implica el aumento anterior.
Análogamente, si la empresa e reduce 1 MWh la cantidad contratada a plazo, el
volumen de energía de esa empresa sensible a las variaciones del precio spot aumenta y
los incentivos de esta compañía para reducir su producción total y mantener un precio
más elevado crecen. Sin embargo, todos los agentes, incluida la empresa e, anticipan
este aumento de precio y reaccionan incrementando su producción para cubrir parte de
la demanda que la empresa e deja de servir. La subida del precio no será, finalmente,
tan elevada.
Por tanto, puesto que la información de la primera etapa es pública, el nivel de
contratos de una cierta empresa afecta no sólo al comportamiento de esa empresa en el
mercado de corto plazo, sino también a las decisiones de todos sus competidores, ya
que todos los agentes pueden prever la influencia de la producción a plazo en el
mercado spot y modificar sus decisiones para adaptarse a los resultados de la primera
98
5.6 Conclusiones
etapa. Estas reacciones son tenidas en cuenta por las empresas cuando toman sus
decisiones de contratación en el mercado a plazo.
Estos resultados se basan en la hipótesis de que la información relativa a los contratos
negociados en el mercado a plazo es pública. Sin embargo, esta información no suele
conocerse en los mercados eléctricos reales, de modo que los agentes no pueden
incorporar en el proceso de toma de decisiones los resultados de sus competidores de
la etapa anterior. En este caso, las empresas no pueden reaccionar ante las decisiones
de contratación del resto de agentes, resultando un equilibrio diferente en el mercado
spot al definido por Allaz y Vila. Dado que el equilibrio de la segunda etapa condiciona
las decisiones de las empresas en el mercado a plazo, el equilibrio en esta primera
etapa también cambia.
99
6
Efectos dinámicos en el
comportamiento estratégico
de los agentes
El modelo de Allaz y Vila –descrito en el capítulo 4 de esta tesis de máster y
generalizado en el capítulo 5– concluye que la existencia de mercados a plazo mejora el
nivel de competencia del mercado spot. Según Allaz y Vila, cuando las empresas
contratan parte de su producción a plazo, la cantidad de energía que puede
beneficiarse de un incremento del precio spot se reduce, de modo que las empresas
tienen menos incentivos para retirar energía y mantener un precio más elevado. Estos
resultados sugieren que los mercados a plazo pueden emplearse como mecanismos
eficientes para mitigar posibles problemas asociados a la estructura oligopolista de
algunos mercados, ya que reducen los incentivos de los agentes para ejercer su poder
de mercado en el spot.
Sin embargo, este efecto procompetitivo es resultado de un juego en el que las
empresas negocian su energía durante un número finito de periodos. En concreto, en el
modelo descrito en el capítulo 4 los agentes compiten solamente en dos instantes,
primero en el mercado a plazo y, posteriormente, en el mercado spot, ignorando que
existen más periodos futuros en los que la interacción definida en el modelo de Allaz y
Vila se repite. Cuando se considera la interacción repetida que existe en los mercados
eléctricos reales, aparecen una serie de efectos que modifican sustancialmente los
resultados del modelo de Allaz y Vila. En este capítulo se desarrolla un modelo no
colusivo que recoge la existencia de mercados posteriores al mercado spot.
101
6 Efectos dinámicos en el comportamiento estratégico de los agentes
6.1 Planteamiento
Una hipótesis crítica en el razonamiento que se ha expuesto en los capítulos anteriores
para concluir que los mercados a plazo mitigan el poder de mercado de los agentes es
la consideración de un horizonte finito de negociación. Sin embargo, los mercados
eléctricos reales presentan una naturaleza repetida, de forma que el número de
periodos en los que las empresas compiten de manera sucesiva tiende a infinito. Al
incorporar la existencia de múltiples periodos en el modelado de la interacción entre
los mercados eléctricos a plazo y los mercados eléctricos al contado, aparecen
diferentes efectos que tienden a compensar los resultados procompetitivos obtenidos
en los modelos anteriores.
Existe una importante línea de investigación que se centra en estudiar la posible
aparición de estrategias cooperativas entre los agentes en el marco de un juego
repetido (véase, por ejemplo, Liski y Montero (2006) o Green y LeCoq (2007)). En los
modelos estáticos los agentes no tienen ningún incentivo para desviarse de la estrategia
óptima que determina el equilibrio de Cournot, ya que en este tipo de juegos no existen
periodos futuros que pudieran modificar su comportamiento óptimo en el problema de
un único periodo. Los efectos colusivos aparecen, por tanto, en modelos dinámicos,
fruto de la interacción repetida entre las empresas en los sucesivos mercados. En estos
modelos los agentes podrían aprender a competir entre ellos de forma menos agresiva
a lo largo del tiempo, coordinando sus estrategias de oferta a través de una colusión
tácita.
Así, si las empresas se coordinan para alcanzar una solución colusiva, sus resultados
globales obtenidos en todo el horizonte mejoran. En esta situación, alguna de las
empresas podría plantearse producir 1 MWh adicional y desviarse unilateralmente de
la estrategia cooperativa anterior. Al hacerlo, la empresa observa que el beneficio
obtenido aumenta, ya que de esta forma es capaz de capturar los precios más elevados
que determina la cooperación entre sus competidores con un mayor volumen de
energía. Siguiendo esta lógica, la empresa continuaría incrementando su producción
hasta alcanzar la cantidad óptima definida por el juego de un periodo, es decir, la
cantidad óptima que produciría la compañía si tomase sus decisiones de manera
individual. Análogamente, el resto de las empresas del mercado llegaría a la misma
solución, de modo que el equilibrio final coincidiría con el equilibrio estático.
Todas las empresas tienen incentivos para romper unilateralmente la cooperación, pero
cuando todas ellas se separan de su estrategia cooperativa, el beneficio global que
obtienen en todo el horizonte considerado se reduce respecto a la solución colusiva.
Por tanto, para que una colusión sea sostenible en el tiempo es necesario que los
agentes sean capaces de detectar desviaciones respecto al comportamiento cooperativo
y puedan desarrollar estrategias de castigo para penalizar a las empresas que se
aparten de él. En un equilibrio colusivo el beneficio global que obtienen las empresas
es mayor que el que obtendrían en un juego no cooperativa, y aún cuando los agentes
tuviesen incentivos para desviarse de la colusión, el riesgo de ser castigados mediante
futuras conductas agresivas debe ser capaz de desanimarlos de romper la cooperación.
102
6.1 Planteamiento
Así, el equilibrio colusivo podrá mantenerse en el tiempo como un equilibrio de un
juego repetido infinitamente.
Todo lo anterior implica que, en la práctica, no resulta sencillo alcanzar soluciones
colusivas. El nivel de información que tienen los agentes no es perfecto, lo que dificulta
que las empresas puedan determinar la estrategia cooperativa óptima que deben
seguir. Además, en un mercado con información imperfecta es complicado detectar y
castigar posibles desviaciones respecto al comportamiento colusivo que, en caso de
darse, acabarían por romper la cooperación entre las empresas. Por ejemplo, es posible
que la información que manejen los agentes no sea suficiente como para que las
empresas productoras puedan distinguir si una caída de los precios del mercado se
debe a una reducción de la demanda de energía de los consumidores o a que sus
competidores se han desviado de la estrategia cooperativa.
Por otro lado, los agentes toman sus decisiones de manera racional, si bien esta
racionalidad está acotada (bounded rationality). La información y los recursos con los
que cuentan las empresas son limitados, y esto condiciona el proceso de toma de
decisiones. En efecto, cuando un agente está maximizando su beneficio global en un
cierto horizonte, la información acerca de los periodos futuros es limitada,
reduciéndose a medida que se consideran periodos más alejados en el tiempo. Esto
hace que los agentes no tengan en cuenta todos los posibles efectos de sus decisiones
presentes y acoten el estudio a las influencias más inmediatas. Así, los agentes pueden
preferir soluciones con peores resultados globales pero con las que obtienen márgenes
más elevados en el presente. En otras palabras, es frecuente que algunas empresas
opten por renunciar a un cierto beneficio futuro si estos ingresos corresponden a
periodos suficientemente alejados, a cambio de capturar un margen mayor en el
periodo actual.
En este sentido, la racionalidad acotada de los agentes puede hacer que poner en
práctica las estrategias de castigo resulte difícil. Si las empresas que se apartan de la
estrategia cooperativa deben ser penalizadas mediante un comportamiento agresivo en
el futuro, algunos agentes pueden considerar que sostener una guerra de precios
durante un cierto número de periodos resulta y muy costoso y decidan no castigar las
desviaciones de sus competidores y acabar alcanzando el equilibrio no cooperativo.
Entonces, hay múltiples factores que condicionan el juego cooperativo y determinan en
qué medida es posible alcanzar una solución colusiva. Existe, de hecho, un folk theorem
que establece que cualquier solución entre el equilibrio del juego no cooperativo y la
colusión perfecta es posible. Esto hace que los resultados de este tipo de estudios
puedan ser discutidos desde diferentes puntos de vista. En este capítulo se presenta un
enfoque alternativo que, sin considerar que los agentes cooperan siguiendo estrategias
diferentes de las que determina el equilibrio de Cournot, representa la existencia de
mercados posteriores al mercado spot.
En el modelo de dos etapas, las empresas se comportan de manera más competitiva en
el mercado spot cuando contratan parte de su producción a plazo porque el volumen
de energía que se ve afectado por las variaciones del precio spot se reduce. Sin
embargo, cuando se considera que existen más mercados posteriores, las empresas
103
6 Efectos dinámicos en el comportamiento estratégico de los agentes
deben tener en cuenta al tomar sus decisiones de producción que el precio del mercado
spot de un cierto periodo puede influir en la valoración de los contratos que se
negociarán en el siguiente periodo. En este contexto, los agentes tienen en cuenta no
sólo el impacto de las variaciones del precio spot en su producción no contratada, sino
también que este precio sirve como referencia para determinar el precio de sus
contratos futuros. Así, el efecto procompetitivo del modelo de Allaz y Vila se
compensa, al menos en parte, por la posibilidad de influir en el precio del siguiente
mercado a plazo, de modo que aunque la producción contratada para un cierto periodo
no esté expuesta al precio del mercado spot de ese periodo, los contratos del siguiente
periodo sí lo están.
Este efecto que se acaba de describir se incluye explícitamente en el modelo que se
propone en el siguiente apartado. Se trata, por tanto, de un juego dinámico no colusivo,
capaz de representar la existencia de periodos futuros de negociación sin considerar
estrategias cooperativas entre los agentes del mercado. Bajo este planteamiento, el
modelo permite analizar el impacto de los mercados a plazo en el comportamiento
estratégico de las empresas que interactúan repetidamente en los sucesivos mercados,
y estudiar si el efecto procompetitivo de la contratación a plazo que se ha identificado
en el modelo estático sigue teniendo consecuencias significativas en las estrategias de
oferta que resulten de este nuevo esquema.
A diferencia de los juegos cooperativos, las hipótesis de este modelo son compatibles
con el enfoque adoptado en los capítulos anteriores. En este caso, no se consideran
estrategias que no resulten de la propia maximización individual de los beneficios de
cada empresa, así que las hipótesis básicas de comportamiento corresponden con las
modeladas por Allaz y Vila. El modelo propuesto se adapta muy bien al planteamiento
de Allaz y Vila, pero incorporando la repetición de mercados que ellos ignoran. Esto
permitirá analizar si los resultados obtenidos en el capítulo 4 con consistentes con la
naturaleza repetida de los mercados eléctricos reales sin introducir estrategias
colusivas que pueden ser discutidas.
6.2 Análisis del comportamiento de los agentes en
mercados sucesivos
Considérese un juego similar al descrito por Allaz y Vila, pero teniendo ahora en
cuenta que tras la negociación de energía en el mercado spot, el esquema definido en el
capítulo 4 se repite en periodos posteriores. En este caso, el modelo consta de múltiples
etapas:
• En el instante inicial considerado las empresas participan en el mercado a plazo
decidiendo la cantidad de energía que van a contratar a plazo y cuya fecha de
( )
entrega tiene lugar durante el periodo t qec,t
104
6.2 Análisis del comportamiento de los agentes en mercados sucesivos
• A continuación, los agentes eligen simultáneamente la cantidad que van a
( )
producir en el mercado spot del periodo t qe,t
de acuerdo con el modelo de
Cournot
• En ese momento, los agentes también deciden en el mercado a plazo su cantidad
(
c
de contratos a plazo con fecha de entrega en el siguiente periodo t+1 qe,t+1
)
• En el periodo t+1 las empresas toman sus decisiones de producción en el
mercado spot, y sus decisiones de contratación para t+2
• El proceso se repite en los sucesivos mercados, decidiendo secuencialmente la
cantidad de energía contratada para t+3, t+4,...t+N, y eligiendo las cantidades
óptimas que van a producir en los diferentes mercados spot que tienen lugar en
cada periodo
La función objetivo de una empresa e que se encuentra tomando sus decisiones de
producción en el spot del periodo t es la maximización de sus beneficios globales
obtenidos a lo largo de todo el horizonte considerado:
(
)
max pts ⋅ qe,t − qec,t − Ce,t +
(
⋅(q
⋅ (q
)
c
s
+ pt+1
⋅ qec,t+1 + pt+1
⋅ qe,t+1 − qec,t+1 − Ce,t+1 +
c
s
+ pt+2
⋅ qec,t+2 + pt+2
c
s
+ pt+N
⋅ qec,t+N + pt+N
donde pts
ptc
)
c
e,t+2 − qe,t+2 − Ce,t+2 + … +
e,t+N
(6.1)
)
− qec,t+N − Ce,t+N
es el precio del mercado spot del periodo t,
es el precio de los contratos de energía negociados en t-1 con fecha de
entrega en t,
qe,t es la producción de la empresa e en el periodo t,
qec,t es la cantidad contratada a plazo por la empresa e en el periodo t-1 con
fecha de entrega en t,
Ce,t es el coste de producción de la empresa e en el periodo t.
Como se expuso en el capítulo 4, la función objetivo de una empresa que se encuentra
decidiendo su producción en el mercado spot del periodo t debe tener en cuenta que
una parte de su energía para ese periodo ya se ha negociado en el mercado a plazo del
periodo anterior. Pero, a diferencia del modelo de un único periodo, los agentes deben
tener en cuenta que existen nuevas oportunidades de contratación y producción en los
mercados posteriores al mercado spot.
El lagrangiano del problema de optimización de cada empresa está dado por:
105
6 Efectos dinámicos en el comportamiento estratégico de los agentes
Le = pts ⋅ ( qe,t − qec,t ) − Ce,t +
(
⋅(q
⋅ (q
)
c
s
+ pt+1
⋅ qec,t+1 + pt+1
⋅ qe,t+1 − qec,t+1 − Ce,t+1 +
c
s
+ pt+2
⋅ qec,t+2 + pt+2
c
s
+ pt+N
⋅ qec,t+N + pt+N
)
c
e,t+2 − qe,t+2 − Ce,t+2 + … +
e,t+N
(6.2)
)
− qec,t+N − Ce,t+N
En un mercado es equilibrio es razonable suponer que el comportamiento de los
agentes no variará significativamente de un periodo a otro. Por tanto, si las condiciones
entre t y t+1 son comparables, las cantidades contratadas a plazo por cada empresa
serán similares. Este modelo supone que la cantidad de contratos que negocia una
empresa no varía a lo largo del tiempo y, así,
qec,t = qec,t+1
(6.3)
En este caso, las empresas deben tener en cuenta que los contratos no tienen una
duración infinita, sino que en cada periodo deben renegociar los contratos del periodo
anterior, y que el precio del mercado spot que tiene lugar cuando los agentes están
negociando en el mercado a plazo puede influir en el precio que obtendrán sus
contratos futuros.
Como se ha explicado en el apartado 4.1, en ausencia de incertidumbre y suponiendo
que los agentes son neutrales al riesgo, el precio de los contratos para un cierto periodo
y el precio del mercado spot de ese periodo no pueden presentar diferencias
importantes. Dado que siempre existe la posibilidad de negociar en uno u otro
mercado, cuando los precios se separan los agentes pueden trasladar su energía al
mercado que les permite obtener mayores beneficios, haciendo con ello que los precios
tiendan a igualarse de nuevo. Sin embargo, resulta complicado predecir perfectamente
el precio de la energía del periodo para el que las empresas se están contratando, de
modo que el precio de los contratos negociados en t con fecha de entrega en t+1
coincidirá con la mejor estimación que hagan los agentes del precio spot en t+1.
En este contexto, el precio del mercado spot de t se convierte en un estimador relevante
del precio que puede resultar en t+1. En efecto, el precio en t+1 depende de una serie de
variables fundamentales, como la demanda de energía de los consumidores en ese
periodo o el coste futuro de los combustibles empleados en las centrales para generar
electricidad. Pero también depende del comportamiento que tendrán los agentes en el
mercado. Incluso ignorando los efectos asociados a la gestión del riesgo de las
empresas, para poder modelar las decisiones y reacciones que ocurren en el mercado
spot de t+1 es necesario estimar el comportamiento estratégico de los agentes. Entonces,
es necesario prever el valor de la pendiente de la función del precio en el siguiente
periodo, que determina la capacidad que tienen los generadores para influir en el
106
6.2 Análisis del comportamiento de los agentes en mercados sucesivos
precio de la energía6. Este parámetro es particularmente difícil de estimar, por lo que
los agentes se basan en el funcionamiento actual del mercado y suponen que las
reacciones de los consumidores no cambian significativamente a lo largo del tiempo.
Por tanto, la mejor estimación de la derivada del precio spot en t+1 respecto a las
decisiones de producción de las empresas en ese mercado es la derivada del precio en
el presente.
La principal dificultad de este problema es que no es sencillo separa el efecto de las
numerosas variables que influyen en la formación del precio. La demanda de energía,
el coste de los combustibles o la producción eólica de cada periodo son sólo algunos
ejemplos del gran número de factores que, junto con el comportamiento de los agentes,
afectan al precio de la energía. Por tanto, resulta muy complicado determinar el
impacto de estas variables y separa el efecto de cada una de ellas. Por ejemplo, es difícil
distinguir en qué medida una bajada del precio spot se debe a una reducción en el
consumo de energía o a un aumento de la elasticidad de la demanda. De hecho,
normalmente, una variación en el precio estará causada por el efecto conjunto de
diversas variables. Por este motivo, los agentes del mercado a plazo toman como
estimador del precio futuro el precio spot del mercado actual, ya que no son capaces de
separa las variables fundamentales que sólo guardan relación con el periodo t de los
parámetros que determinan el comportamiento estratégico de las empresas.
De este modo, la mejor estimación del comportamiento futuro de las empresas es el
precio spot del mercado que está teniendo lugar cuando deciden sus contratos, y el
precio del mercado spot de un cierto periodo sirve como referencia para el precio de los
contratos que se están negociando en ese periodo para su entrega en un momento
futuro. Así, el precio de la energía a plazo con fecha de entrega en t+1 se puede
descomponer en dos términos:
• una cierta función de las variables fundamentales en t+1
• el precio del mercado spot de t, que representa la mejor estimación del
comportamiento de los agentes en t+1
c
pt+1
= f ( fundamentalest+1 ) + pts
(6.4)
c
c
y pts o, lo que es lo mismo, entre pt+1
y qe,t ,
Por tanto, existe una relación entre pt+1
de manera que las decisiones de las empresas en el mercado spot del periodo t influyen
en la remuneración de sus contratos a plazo para el siguiente periodo.
Por otro lado, cuando los agentes participan en el mercado spot de t+1, el spot de t ya ha
pasado, y las decisiones en este segundo mercado spot se toman sin tener en cuenta lo
sucedido en t. En consecuencia, las decisiones de las empresas en cada mercado spot
6
Véase el capítulo 3 para una explicación más detallada.
107
6 Efectos dinámicos en el comportamiento estratégico de los agentes
son independientes de las del periodo anterior, de modo que los resultados obtenidos
en t no influyen en los que se obtendrán en el siguiente periodo.
Teniendo en cuenta todo lo anterior, al derivar la función lagrangiana respecto de la
cantidad producida en t –que es la variable de decisión de los generadores en el
mercado spot de t– se obtiene la siguiente condición de optimalidad para cada
empresa e:
∂C
∂Le
∂p s
= t ⋅ qe,t − qec,t + pts − e,t +
∂qe,t ∂qe,t
∂qe,t
(
)
∂p c
+ t+1 ⋅ qec,t = 0
∂qe,t
(6.5)
De la ecuación (6.4):
c
∂pt+1
∂p s
= t
∂qe,t ∂qe,t
(6.6)
Y, por tanto,
∂C
∂pts
∂p s
⋅ qe,t − qec,t + pts − e,t + t ⋅ qec,t = 0
∂qe,t
∂qe,t ∂qe,t
(
)
(6.7)
Reagrupando términos:
∂C
∂pts
⋅ qe,t + pts − e,t = 0
∂qe,t
∂qe,t
(6.8)
Es decir, cuando los agentes tienen en cuenta la influencia que tienen sus decisiones de
producción en el precio de sus contratos futuros, la solución óptima para cada empresa
coincide con la solución del modelo de Cournot. Al tener en cuenta la existencia de
mercados posteriores al mercado spot, aparece un término adicional que el modelo de
Allaz y Vila ignora, y que anula el efecto procompetitivo de los contratos a plazo que
resultaba del modelo de dos etapas.
En estas condiciones, una empresa que tiene parte de su producción contratada a plazo
y decide aumentar sus ventas en el spot considerando que una bajada de precio no
afectará a la energía que ya ha negociado previamente en la etapa anterior, debe
también tener en cuenta que ese precio más bajo será el que sirva de referencia para
determinar el precio de sus contratos en el siguiente periodo. Entonces, cuando una
empresa está decidiendo su producción en el mercado spot debe comparar tres
términos:
108
6.2 Análisis del comportamiento de los agentes en mercados sucesivos

• El beneficio que obtiene por cada megavatio-hora generado  pts −


∂Ce,t 
,
∂qe,t 
representado por el área verde de la Figura 6.1.
• La reducción de ingresos que una bajada de precio supone sobre toda su
 ∂pts
⋅ qe,t − qec,t
∂
q
 e,t
producción no contratada para este periodo 

(

)  , representada

por el área roja de la Figura 6.1.
• La reducción en el precio de los contratos del siguiente periodo asociada a una
 ∂pts c 
⋅ qe,t  ,

∂
q
e
,
t


bajada del precio spot cuando la producción de la empresa aumenta 

representada por el área naranja de la Figura 6.1.
ps
∆ps
Coste de producción
Precio de la energía
qe,tc
∆qe,t
qt
Figura 6.1: Efectos del incremento de producción sobre el beneficio de una empresa con contratos a plazo en
múltiples periodos
Este último término, que representa la reducción de ingresos que tiene los contratos del
siguiente periodo cuando el precio del mercado spot actual baja, reduce los incentivos
de las empresas para aumentar su producción. Al considerar el impacto que tienen las
decisiones actuales en la remuneración futura que obtendrá la empresa, ésta encuentra
que resulta rentable retirar cantidad del mercado spot para conseguir un precio más
alto en los contratos del siguiente periodo. La decisión óptima de los agentes buscará,
por tanto, no sólo maximizar el beneficio que obtiene por sus ventas en el mercado de
corto plazo, sino también conseguir unos ingresos elevados de sus contratos futuros.
De modo que las empresas tienen un incentivo adicional para mantener el precio spot
alto y conseguir así contratar más tarde a un precio superior.
Este efecto dinámico anula la capacidad de los contratos a plazo para mitigar el poder
de mercado de los agentes que resulta del modelo de Allaz y Vila, y el equilibrio del
mercado entonces coincide con el equilibrio del modelo de una etapa. El efecto
procompetitivo de la contratación a plazo se basa en la hipótesis de que los agentes no
tienen en cuenta que en el siguiente periodo tendrán que renegociar sus contratos y
109
6 Efectos dinámicos en el comportamiento estratégico de los agentes
que el precio que recibirán estos contratos depende del precio spot del periodo actual.
En otras palabras, el modelo de Allaz y Vila ignora la naturaleza repetida que
presentan los mercados eléctricos reales. Sin embargo, cuando se incorpora al modelo
de Allaz y Vila la interacción repetida que existe entre los mercados eléctricos a plazo y
los mercados eléctricos al contado, los resultados que se obtienen cambian
sustancialmente. En concreto, en el modelo presentado en este apartado la existencia
de un mercado a plazo en el que las empresas pueden negociar parte de su energía no
modifica el comportamiento estratégico de los agentes en el mercado spot.
6.3 Conclusiones
El modelo desarrollado por Allaz y Vila concluye que la existencia de mercados a plazo
reduce los incentivos de las empresas para ejercer su poder de mercado cuando
deciden su producción en el spot. Sin embargo, este modelo ignora que el número de
periodos en los que las empresas negocian su energía no es finito, sino que existen
múltiples mercados que suceden al mercado spot de la segunda etapa del modelo
anterior.
Existen diversos autores que indican que cuando se considera la naturaleza real de los
de los mercados eléctricos, en los que las empresas interactúan repetidamente, pueden
aparecer estrategias cooperativas que no sólo anulan el efecto procompetitivo del
modelo de dos etapas, sino que incluso pueden hacer en algunos casos que aparezcan
efectos colusivos que no existirían si los agentes no tuvieran la posibilidad de
participar en una mercado a plazo. Ahora bien, este tipo de estrategias colusivas son
difíciles de poner en práctica, de modo que los resultados de estos modelos pueden ser
discutidos.
En este capítulo se ha presentado un modelo que, sin considerar la posible cooperación
entre los agentes del mercado, incorpora la dinámica repetida del problema. Partiendo
del modelo de Allaz y Vila, se ha añadido la existencia de un mercado a plazo después
de cada mercado spot. En este contexto, las empresas deben tener en cuenta que el
precio spot de cada periodo constituye el mejor estimador del comportamiento futuro
de los agentes y que, por tanto, este precio sirve como referencia para el precio de los
contratos se están negociando para el siguiente periodo. Se trata de una modificación
sencilla del modelo de Allaz y Vila que incorpora una representación más realista del
funcionamiento de los mercados eléctricos. Sin embargo, al hacerlo, los resultados
obtenidos cambian sustancialmente.
Cuando las empresas tienen en cuenta que los ingresos que obtendrán los contratos
negociados para un cierto periodo dependen del precio spot del periodo anterior, el
efecto procompetitivo descrito en el capítulo 4 se compensa por la posibilidad de
influir en el precio del siguiente mercado a plazo. Es decir, los agentes tienen en cuenta
que, aunque la producción que han contratado a plazo en la etapa anterior no se verá
afectada por las variaciones del precio en este mercado, la energía a plazo del siguiente
periodo sí lo hará. Entonces, la decisión óptima de cada empresa incluirá el impacto de
una bajada de precio tanto en sus ventas en el mercado spot, como en los contratos del
110
6.3 Conclusiones
siguiente periodo. Esto reduce los incentivos de las empresas para producir 1 MWh
adicional incluso cuando la mayor parte de su producción ya haya sido contratada a
plazo. El equilibrio del mercado en este caso coincide con el equilibrio del modelo de
Cournot. Por tanto, al considerar la existencia de mercados posteriores al spot se
concluye que la mera existencia de mercados a plazo no reduce los incentivos de las
empresas para ejercer su poder de mercado.
111
7
Conclusiones
El objetivo marcado en el origen de esta tesis de máster consistía en estudiar las
posibles influencias de los mercados a plazo sobre las estrategias de oferta de los
agentes que operan en un mercado spot. Los desarrollos presentados permiten
profundizar en el problema de la interacción entre los mercados eléctricos a plazo y los
mercados eléctricos al contado, y ayudan comprender el comportamiento estratégico
de las empresas que contratan parte de su producción a plazo.
En los primeros capítulos de la tesis de máster se ha retratado la situación que
experimenta el sector eléctrico en la actualidad, en el que muchos países han procedido
ya a introducir mecanismos de competencia. Esto ha hecho que las empresas de
generación se enfrenten a la necesidad de planificar su operación en un marco
liberalizado, donde tienen que competir en los diferentes mercados con el resto de
compañías.
Muchos de estos mercados cuentan con mercados a plazo consolidados, que ofrecen la
posibilidad de negociar la compra-venta de energía mediante transacciones a plazo. En
este caso, los agentes pueden acordar la venta de una cierta cantidad de electricidad a
un precio fijo para un periodo futuro. Sin embargo, la gran mayoría de los modelos que
representan el comportamiento del mercado eléctrico en competencia imperfecta no
tienen en cuenta la existencia de un mercado a plazo, que puede influir en el
comportamiento de los agentes en el mercado spot.
En el capítulo 4 de esta tesis de máster se describe el modelo desarrollado en Allaz y
Vila (1993), que constituye una de las principales referencias que se encuentran en la
literatura sobre el problema de la interacción entre los mercados a plazo y los mercados
spot. Se basa en un juego de dos etapas que analiza el efecto que tienen los contratos
negociados en los mercados a plazo sobre las decisiones de los agentes con poder de
113
7 Conclusiones
mercado cuando operan en el spot, considerando dos únicas empresas simétricas con
costes de producción lineales, y representando el precio como una función lineal de la
demanda de pendiente unitaria.
El resultado fundamental del modelo de Allaz y Vila es que la existencia de mercados a
plazo incrementa el nivel de competencia entre los agentes. El modelo muestra que
contratar parte de su producción a plazo hace que las empresas adopten estrategias
más agresivas que dan como resultados una mayor generación y unos precios más
reducidos. Este efecto procompetitivo se debe a que las variaciones del precio spot no
afectan a la producción que ha sido negociada previamente y que recibe el precio fijado
en el mercado a plazo, por lo que los agentes son menos sensibles a la elasticidad del
precio y tienden a aumentar su producción. Por tanto, según el modelo de Allaz y Vila,
los mercados a plazo reducen los incentivos de las empresas para ejercer su poder de
mercado.
Este resultado implica que las empresas obtienen menores beneficios cuando deciden
realizar transacciones a plazo y, sin embargo, deciden negociar contratos. La
posibilidad de participar en un mercado a plazo crea un dilema del prisionero para los
agentes. Cuando sólo una empresa negocia un cierto volumen de energía a plazo, el
beneficio que obtiene aumenta respecto al caso en el que no se contrataba, mientras que
los resultados de la otra compañía empeoran notablemente. Por tanto, cada agente
tiene incentivos para contratar un parte de su producción. Sin embargo, cuando ambos
participan en el mercado a plazo, su beneficio disminuye respecto al caso sin contratos.
Las empresas saben que podrían capturar mayores márgenes si ninguna de las dos se
contratase, pero la posibilidad de que sólo su competidora lo haga incentiva a cada
empresa a negociar parte de su energía a plazo.
En el capítulo 5 se ha generalizado el modelo del capítulo anterior. El modelo de Allaz
y Vila está desarrollado para unas condiciones de mercado muy rígidas. Este modelo
considera la existencia de dos únicas empresas simétricas cuyas curvas de costes están
dadas por funciones lineales de su producción, y donde el precio del mercado está
caracterizado por una función lineal de la demanda de pendiente unitaria. Estas
condiciones no se adaptan a la mayoría de los mercados eléctricos existentes, lo que
limita enormemente las posibles aplicaciones del modelo. En el capítulo 5 se ha
presentado un desarrollo original que generaliza la formulación del modelo de Allaz y
Vila, extendiendo el estudio al caso en el que operan un número E indeterminado de
empresas caracterizadas por una curva general de costes, e incorporando una función
lineal con pendiente α para representar el precio de mercado.
La generalización del modelo permite analizar con mayor detalle las reacciones de los
agentes ante una variación en la producción a plazo de una cierta empresa. De acuerdo
con el efecto procompetitivo identificado en el modelo de Allaz y Vila, cuando una
empresa decide aumentar la cantidad de sus contratos, su potencia inframarginal
sensible a una bajada del precio spot se reduce y, por tanto, la empresa incrementa su
producción total, haciendo con ello que el precio del mercado baje. Por otro lado,
cuando una empresa modifica su contratación en el mercado a plazo, todos los agentes
del spot anticipan la variación en la producción de esta empresa y su influencia en el
114
7 Conclusiones
precio de corto plazo. Los cambios en el precio spot afectarán a la producción no
contratada de todas las empresas que operan en el mercado spot, incluida la propia
empresa que ha variado sus contratos, que reaccionan cambiando su producción para
amortiguar el efecto de estas variaciones. Por tanto, el volumen de contratos de una
cierta empresa afecta no sólo al comportamiento de esa empresa en el mercado de corto
plazo, sino también a las decisiones de todos sus competidores, ya que todos los
agentes pueden prever la influencia de la producción a plazo en el mercado spot y
modificar sus producciones para adaptarse a los resultados del mercado a plazo. Las
empresas incorporan estas reacciones en el proceso de decisión de la primera etapa, de
forma que cuando deciden la cantidad de energía que van a contratar a plazo tienen en
cuenta la influencia que sus decisiones de contratación tendrán en el spot.
Allaz y Vila no tienen en cuenta algunas consideraciones cruciales para representar de
forma realista el comportamiento de los agentes que modifican sustancialmente sus
resultados. Por un lado, para que las reacciones que se han comentado sean posibles es
necesario que la información relativa a los contratos negociados en el mercado a plazo
sea pública. Esta información no suele conocerse en los mercados eléctricos reales, de
modo que los agentes no pueden tomar sus decisiones óptimas de producción a partir
de los resultados de la etapa anterior, lo que altera los resultados del modelo de Allaz y
Vila.
Por otro lado, más importante que el problema de la información del mercado a plazo
en el análisis de las conclusiones obtenidas en los capítulos 4 y 5 resulta el hecho de
que el efecto procompetitivo del modelo de Allaz y Vila es resultado de un juego en el
que las empresas negocian su energía durante un número finito de periodos. En
concreto, en el modelo estudiado los agentes compiten solamente en dos instantes,
primero en el mercado a plazo y, posteriormente, en el mercado spot, ignorando que
existen más periodos futuros en los que el problema de la interacción entre mercados
se repite. Cuando se considera la naturaleza repetida de la negociación en los mercados
eléctricos, aparecen una serie de efectos que cambian radicalmente los resultados del
modelo de Allaz y Vila.
En el capítulo 6 se han analizado las implicaciones de ignorar la existencia de múltiples
periodos de negociación. Por un lado, existe un buen número de autores que estudian
la posible aparición de estrategias cooperativas entre los agentes que interactúan
repetidamente. Estos trabajos concluyen que al tener en cuenta la existencia de un
número infinito de periodos de negociación, las empresas pueden coordinar sus
estrategias y alcanzar una colusión tácita que anula el efecto procompetitivo del
modelo de dos etapas. Incluso se han descrito algunos efectos colusivos que sólo
pueden darse gracias a la existencia de mercados a plazo. Sin embargo, este tipo de
estrategias son difíciles de llevar a la práctica por distintos motivos, que van desde la
información imperfecta que manejan los agentes hasta la racionalidad acotada de los
mismos cuando toman sus decisiones, por lo que los resultados de este tipo de
modelos puede ser discutido.
En esta tesis de máster, en cambio, se ha desarrollado un modelo original que, sin
considerar la posible cooperación entre los agentes del mercado, incorpora la dinámica
115
7 Conclusiones
repetida del problema. Partiendo del modelo de Allaz y Vila, se ha añadido la
existencia de un mercado a plazo después de cada mercado spot. En este contexto, las
empresas deben tener en cuenta que el precio spot de cada periodo constituye el mejor
estimador del comportamiento futuro de las empresas y que, por tanto, este precio
sirve como referencia para el precio de los contratos que se están negociando para el
siguiente periodo. Cuando las empresas consideran que los ingresos que obtendrán los
contratos para un cierto periodo depende del precio spot del periodo anterior, el efecto
procompetitivo del modelo de Allaz y Vila se compensa por la posibilidad de influir en
el precio del siguiente mercado a plazo. El equilibrio del mercado en este caso coincide
con el equilibrio del modelo de Cournot y, entonces, la existencia de mercados a plazo
no reduce por sí misma los incentivos de las empresas para ejercer su poder de
mercado.
116
Referencias
Allaz, B. y Vila, J. L. (1993). Cournot competition, forward markets and efficiency. Journal of
Economy Theory 59, p. 1-16.
Amaya, F., Rodilla, P., García-González, J. y Vázquez, C. (2006). The strategic effects of
forward markets on oligopolistic electricity equilibria. 1st Enerday Conference on
Energy Economics and Technology, Dresden.
Le Coq, C. (2004). Long-term supply contracts and collusion in the electricity market.
Working Paper Series in Economics and Finance 552. Stockholm School of
Economics.
Von der Fer, N-H. M. y Harbord, D. (1993). Spot market competition un the UK electricity
industry. Economic Journal 103, p. 531-546.
Fernández, B. (2002). Modelo para la programación de unidades de una empresa generadora en
un sistema eléctrico liberalizado. Proyecto Fin de Carrera. E.T.S. de Ingenieros
Industriales, Universidad Politécnica de Madrid.
Ferreira, J. L. (2001). Strategic interaction between futures and spot markets. Journal of
Economic Theory 108, p. 141-151.
Green, R. (1999). The electricity contract market in England and Wales. Journal of Industrial
Economics 47, p. 107-124.
Green, R. y le Coq, C. (2007). The length of contracts and collusion. Center for the Study of
Energy Markets, paper CSEMWP-154.
Liski, M. y Montero, J. P. (2006). Forward trading and collusion in oligopoly. Journal of
Economic Theory 131, p. 212-230.
117
Referencias
Mahenc, P. y Salanié, F. (2004). Softening competition through forward trading. Journal of
Economic Theory 116, p. 282-293.
Newbery, D. (1998). Competition, contracts and entry in the electricity spot market. RAND
Journal of Economics 29, p. 726-749.
Pérez-Arriaga, I. J. (1998). Visión global del cambio de regulación. Monográfico sobre la
liberalización del sector eléctrico. Anales de Mecánica y Electricidad LXXV,
fascículo II.
Schweppe, F. C., Caramanis, M. C., Tabors, R. D. y Bhon, R. E. (1988). Spot pricing of
electricity. Kluwer Academic Publishers.
Ventosa, M. (2001). Modelado de la explotación de la generación en mercados eléctricos
liberalizados mediante el problema complementario. Tesis doctoral. Universidad
Pontificia Comillas de Madrid.
Wolak, F. A. (2000). An empirical analysis of the impact of hedge contracts on bidding
behaviour in a competitive electricity market. International Economic Journal 14,
p. 1-39.
Zhang, Y. y Zwart, G. (2006). Market power mitigation contracts and contrats duration.
mimeo, University of Toulouse.
118