dieléctricos
Anuncio

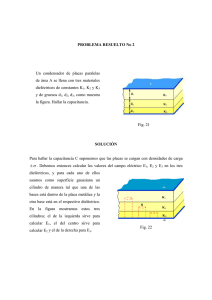
UAP FACULTAD DE INGENIERIAS Y ARQUITECTURA ESCUELA PROFESIONAL INGENIERÍ INGENIERÍA AMBIENTAL ASIGNATURA: FÍSICA III CÓDIGO: 24-211, IV CICLO, 2HR. TEÓRICAS Y 2HR. PRÁCTICAS SESIÓN : 5 Y 6 (SEMANA 6) TEMA: CONDENSADORES Y DIELÉCTRICOS DOCENTE : LIC. JOSÉ LUNA DE LA CRUZ ESQUEMA TEMÁTICO OBJETIVOS DE LA SESIÓN SABER PREVIO (ALCANCE DE CLASE • • • • ANTERIOR) TEMAS: CONDENSADORES DIELÉCTRICOS ENERGÍA DE UN CAPACITOR RESUMEN, COMENTARIOS, TAREAS Y OTROS ALCANCES PARA LA SIGUIENTE SESIÓN OBJETIVO DE LA SESIÓN PROPORCIONAR AL ESTUDIANTE LOS CONOCIMIENTOS NECESARIOS DE LA FÍSICA DE CAMPOS ELÉCTRICOS Y MAGNÉTICOS PARA UNA MAYOR COMPRENSIÓN DE LOS DIFERENTES FENÓMENOS QUE GENERA, PIERDEN Y TRANSFORMAN ENERGÍA POR DIFERENTES FORMAS. LOGRAR QUE EL ESTUDIANTE DESARROLLE SU CRITERIO DE ANÁLISIS PARA RESOLVER PROBLEMAS Y APLICARLOS DE MANERA PRÁCTICA DURANTE EL DESARROLLO DE SU PROFESIÓN COMO INGENIERO. OBJETIVO DE LA SESIÓN LOGRAR QUE EL ESTUDIANTE SEA CAPAZ DE MANIPULAR EN FORMA ADECUADA LOS INSTRUMENTOS PARA DEMOSTRAR LAS LEYES FÍSICAS EN EL CAMPO DE LA ELECTRICIDAD Y MAGNETISMO. REVISIÓN • POTENCIAL ELÉCTRICO. • ENERGÍA POTENCIAL ELÉCTRICA • DIFERENCIAS DE POTENCIAL • SUPERFICIES EQUIPOTENCIALES • ELECTRONVOLT CAPACITANCIA Un capacitor es un dispositivo capaz de almacenar carga eléctrica y consiste en dos objetos conductores (generalmente placas u hojas) colocados uno cerca de otro, pero sin que estén en contacto Los capacitores se usan ampliamente en los circuitos electrónicos. CAPACITANCIA CAPACITANCIA Almacenan carga que posteriormente se puede liberar , como en un flash de cámara y como respaldo de energía en las computadoras para cuando falla la potencia. Los capacitores bloquean los excesos de carga y energía para proteger los circuitos. CAPACITANCIA Capacitores muy pequeños sirven como memoria para los unos y ceros del código binario en la memoria de acceso aleatorio (RAM) de las computadoras. Los capacitores también tienen muchas otras aplicaciones. CAPACITANCIA CAPACITANCIA Un capacitor simple consiste en un par de placas paralelas de área A separados por una pequeña distancia d. Con frecuencia , las dos placas están enrolladas de la forma de un cilindro con papel u otro aislador para separar las placas. El símbolo ┤├ representa un capacitor CAPACITANCIA CAPACITANCIA Otro símbolo para capacitor que se utiliza a menudo es: ┤(— Si a través de un capacitor se aplica un voltaje conectando el capacitor a una batería con alambres conductores, las dos placas rápidamente quedan cargadas, una carga adquiere carga negativa, la otra cantidad igual de carga positiva. CAPACITANCIA +Q -Q + + + + - 12 V + C - - + V CAPACITANCIA En consecuencia todo el voltaje de la batería aparece através del capacitor. Para un capacitor dado, la cantidad de carga Q que adquiere cada placa es proporcional a la magnitud de la diferencia de potencial V entre ellas Q=CV C: es la cte de proporcionalidad y se denomina capacitancia. CAPACITANCIA La unidad de capacitancia es coulomb por voltio, y a esta unidad se le llama farad F. Los capacitores comunes tienen capacitancia en el rango en el rango de 1pF= picofarad=10-12 F. Fue Volta quien sugirió por primera vez la relación expresada Q=CV. CAPACITANCIA Otra forma de capacitancia es: C=∈oA/d , donde representar la ∈o=8.85x10-12 C2/N2m2 Es decir el valor depende del tamaño, forma y posición relativa de los conductores y también del material que los separa. C depende de A, D y no de Q y V PROBLEMA PROPUESTO 1.- Calcule la capacitancia de un capacitor de placas paralelas cuyas placas miden 20cm y 30 cm y están separadas por una brecha de aires de 1 mm. A C =∈0 d PROBLEMA PROPUESTO 2.- Cual es la carga de cada placa, si a través de las placas se conecta una batería de 12 V. Capacitor de placas paralelas cuyas placas miden 20cm y 30 cm y están separadas por una brecha de aires de 1 mm. Q = C .V PROBLEMA PROPUESTO 3.- Cual es el campo eléctrico entre las placas, si a través de las placas se conecta una batería de 12 V y están separadas por una brecha de aires de 1 mm. V E= d PROBLEMA PROPUESTO 4.- Estime el área que de las placas que se necesita para lograr una capacitancia de 1F, si a través de las placas se conecta una batería de 12 V y están separadas por una brecha de aires de 1 mm. A= C .d ∈0 COMBINACION DE CONDENSADORES Una combinación de condensadores en un circuito puede reemplazarse por un solo condensador que almacene la misma cantidad de carga para una determinada diferencia de potencial. Decimos entonces que el condensador sustituto posee una capacidad equivalente o efectiva. COMBINACION DE CONDENSADORES Esto es, si una combinación de condensadores inicialmente descargados se conecta a una batería, la carga Q que fluye a través de ella según se va cargando el sistema de condensadores es la misma que la que fluiría a través de la citada batería si se conectara a un condensador único con una capacidad equivalente. COMBINACION DE CONDENSADORES La capacidad equivalente de condensadores en paralelo es : C eq = Va Q Q1 + Q2 Q1 Q2 = = + = C1 + C 2 V V V V a C1 Vb dos b C2 COMBINACION DE CONDENSADORES La capacidad equivalente condensadores en serie es : de dos 1 Q Q Q Q 1 1 = = = + = + C eq V V1 + V2 (Q / V1 ) (Q / V2 ) C1 C 2 Va a C1 C2 Vb b PROBLEMA PROPUESTO 5.- Determinar la carga equivalente, si es un circuito en paralelo y los condensadores son de 6 y 12 µF (V=12V). C eq = Q Q1 + Q2 Q1 Q2 = = + = C1 + C 2 V V V V PROBLEMA PROPUESTO 6.- Determinar la carga equivalente, si es un circuito en serie y los condensadores son de 6 y 12 µF (V=12V). C eq = Q Q1 + Q2 Q1 Q2 = = + = C1 + C 2 V V V V DIELÉCTRICOS Hasta ahora se ha analizado los capacitores como si no hubiese nada entre las placas que lo conforman. Debemos saber que la presencia de un material alteran la capacidad o características de un capacitor y posiblemente el campo eléctrico que hay en él. DIELÉCTRICOS Es por ello que el objeto de esta clase es conocer como es que actúan estos dispositivos electrónicos que pueden tener entre las placas distintos materiales. Así conoceremos dieléctricos. a los denominados ¿Quién fue el primer investigador? DIELÉCTRICOS Fue Michael Faraday, en 1937, quien primero investigó el efecto de llenar el espacio entre las placas de un capacitor con un dieléctrico. Faraday construyó dos capacitores idénticos , llenando uno con un dielétrico y el otro con aire en condiciones normales. DIELÉCTRICOS Cuando ambos capacitores fueron cargados a la misma diferencia de potencial, los experimentos de Faraday demostraron que la carga en el capacitor con el dieléctrico era mayor que aquella en + el otro. + + + - q1 + + q dieléctrico Aire + - - q>q1 - + DIELÉCTRICOS Puesto que q es mayor para la misma V con el dieléctrico presente, se sigue de la relación C=q/V que la capacitancia de un capacitor aumenta si se coloca un dieléctrico entre las placas. Es de suponer que el dieléctrico llena completamente el espacio entre las placas. + + + - q dieléctrico + - DIELÉCTRICOS El factor adimensional por el cual crece la capacitancia en relación con su valor C0 cuando no hay un dieléctrico presente , se llama constante dieléctrica Ke. + + + Ke=C/C0 - q dieléctrico + - DIELÉCTRICOS La constante dieléctrica es una propiedad fundamental del material dieléctrico y es independiente del tamaño o la forma del conductor. El aire y el vacío son equivalentes en sus efectos dieléctricos. APLICACIONES DIELÉCTRICOS Los dieléctricos se utilizan en la fabricación de condensadores, para que las cargas reaccionen. Cada material dieléctrico posee una constante dieléctrica k. Tenemos k para los siguiente dieléctricos: vacío tiene k = 1; aire (seco) tiene k = 1,00059; teflón tiene k = 2,1; nylon tiene k = 3,4; papel tiene k = 3,7; agua tiene k = 80. APLICACIONES DIELÉCTRICOS Los dieléctricos más utilizados son el aire, el papel y la goma. La introducción de un dieléctrico en un condensador aislado de una batería, tiene las siguientes consecuencias: Disminuye el campo eléctrico entre las placas del condensador. Disminuye la diferencia de potencial entre las placas del condensador, en una relación Vi/k. APLICACIONES DIELÉCTRICOS Aumenta la diferencia de potencial máxima que el condensador es capaz de resistir sin que salte una chispa entre las placas (ruptura dieléctrica). Aumento por tanto de la capacidad eléctrica del condensador en k veces. La carga no se ve afectada, ya que permanece la misma que ha sido cargada cuando el condensador estuvo sometido a un voltaje. DIELÉCTRICOS DIELÉCTRICOS DIELÉCTRICOS Así, primero se conecta el capacitor a la batería y cuando se carga (q), entonces se procede a desconectar. Luego se coloca una lámina dieléctrica, la carga permanece constante, pero la diferencia de potencial cambia. El potencial cambia o disminuye en un factor Ke de V a V/Ke después de haber insertado el dieléctrico. DIELÉCTRICOS El propósito del capacitor es almacenar energía, entonces su capacidad aumenta gracias al dieléctrico, el cual le permite almacenar un factor Ke mas de carga para una misma diferencia de potencial. Sin embargo, la presencia del dieléctrico limita también la diferencia potencial que puede mantenerse entre las placas. DIELÉCTRICOS Si se excede este límite, el material dieléctrico se perfora, resultando en una trayectoria conductora entre las placas. Cada material dieléctrico tiene una resistencia o rigidez dieléctrica característica que es el valor máximo del campo eléctrico que puede soportar sin perforación. DIELÉCTRICOS En un capacitor de placas paralelas lleno con dieléctrico, la capacitancia es de: K e ∈0 A C= d Ke=1, corresponde al vacío entre las placas DIELÉCTRICOS Para una carga puntual q incrustada en el dieléctrico, el campo eléctrico es: E= 1 q 4πK e ∈0 r 2 Esta es la ecuación del campo total en el dieléctrico. DIELÉCTRICOS De modo similar, el campo eléctrico cerca de la superficie de un conductor cargado y aislado inmerso en un dieléctrico es: E= σ K e ∈0 PROBLEMA PROPUESTO 7.- Un capacitor de placas paralelas cuya capacitancia C0 es de 13.5 pF tiene una diferencia de potencial V=12.5 V entre sus placas. La batería de carga se desconecta ahora y se desliza una lámina de porcelana (Ke=6.5) entre las placas como se muestra en la figura. ¿Cuál es la energía almacenada de la unidad, tanto antes como después de haber introducido la lamina?. PROBLEMA PROPUESTO 1º Datos: C0=13.5 pF, V=12.5 V Ke=6.5 2º Ecuación: U i = 1 .C oV 2 2 y q2 q2 Ur = = 2C 2k e C 0 W = Ui − Ur y 3º Reemplazar datos 4º Respuesta: W=1055pJ-162pJ PROBLEMA PROPUESTO Un capacitor de placas paralelas de área A y separación d entre las placas. Entre ellas se aplica una diferencia de potencial V0. entonces se desconecta la batería, y se coloca una lámina dieléctrica de espesor b y constante dieléctrica ke entre las placas PROBLEMA PROPUESTO A=115cm2, d=1.24cm, b=0.78cm Ke=2.61 y Vo=85.5 V PROBLEMA PROPUESTO ¿Cual es la capacitancia C0 antes de insertar la lámina?. ∈ A C0 = ∈0=8.55x10-12F/m ∈0 d C0=8.21pF PROBLEMA PROPUESTO ¿Qué carga libre aparece en las placas? q = C 0V0 q=702pC PROBLEMA PROPUESTO ¿Cuál es el campo eléctrico E0 en los espacios entre las placas y la lámina dieléctrica?. Sol: Aplicando la ley de Gauss ∫ E .dA = Ke=1, por no haber dieléctrico E0= 6900 V/m q ∈0 K e PROBLEMA PROPUESTO ¿Cuál es la diferencia de potencial entre las placas después de haber introducido la lámina? − V = ∫ Edl = E 0 ( d − b ) + Eb + V=52.3V PROBLEMA PROPUESTO ¿Cuál es la capacitancia con la lámina en su lugar? −10 q 7.02 x10 − C C= = V 52.3V C=1.34x10-11 pF RESUMEN DE LA SESIÓN • CONDENSADORES • DIELÉCTRICOS • ENERGÍA DE UN CAPACITOR TAREA O PROBLEMAS TAREA: 1)Realizar informe de laboratorio y presentar en la siguiente clase. Debe contemplar teoría de errores. ALCANCES PARA SIGUIENTE SESIÓN LA • ELECTRODINÁMICA • CORRIENTE ELÉCTRICA PREGUNTAS GRACIAS LIC. JOSÉ LUNA DE LA CRUZ E-mail: lunajosern@hotmail.com Cel: Cel: 990980588