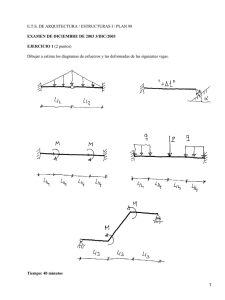
Taller flexión

TALLER DE FLEXIÓN
Resuelva los siguientes ejercicios teniendo en cuenta:
a)
Elaborar diagrama de cada situación que analice.
b)
Indique las ecuaciones a utilizar.
c)
Señale o marque sus respuestas.
d)
Emplee las unidades correspondientes.
e)
Los valores que se manejen en la resolución de problemas deben salir del enunciado del
problema o ser el resultado de la aplicación de una formula.
Cualquier inquietud enviarla a juancjimenez@utp.edu.co o personalmente en horario de consulta.
1. G 5.5-17 Una viga en voladizo AB, con
carga uniforme y una carga concentrada (véase
la figura) está hecha con sección en canal.
Encuentre el esfuerzo de tensión máximo σt, y
el esfuerzo de compresión máximo σc, si la
sección transversal tiene las dimensiones
indicadas y el momento de inercia respecto al
eje z (el eje neutro) es I = 2.81 pulg4 (Nota: la
carga uniforme representa el peso de la viga).
Respuesta: σt = 4240 psi σc = 14940 psi.
3. B 4.7 Dos fuerzas verticales se aplican a una
viga con la sección transversal que se muestra
en la figura. Determine los esfuerzos máximos
de tensión y compresión en la porción BC de la
viga. Respuesta: 8.82 ksi, -14.71 ksi.
2. G 5.5-21 Una viga T está soportada y
cargada como se ve en la figura. La sección
transversal tiene ancho b = 2 ½ pulg, altura h =
3 pulg y espesor t = ½ pulg. Determine los
esfuerzos máximos de tensión y compresión en
la viga. Respuesta: σt = 11520 psi σc = 8640
psi
4. G 5.5-22 Una viga en voladizo AB con
sección transversal rectangular tiene un agujero
longitudinal en toda su longitud (véase la
figura). La viga soporta una carga P = 600 N.
La sección transversal es de 25 mm de ancho y
50 mm de altura; el agujero tiene un diámetro
de 10 mm.
Encuentre los esfuerzos de flexión en la parte
superior de la viga, en la parte superior del
agujero y en la parte inferior de la viga.
Respuesta: σ = 25.1 MPa, 17.8 MPa, -23.5
MPa.
4. G 5.6-17 Determine las razones de los pesos
de tres vigas que tienen la misma longitud, son
del mismo material, están sometidas al mismo
momento flexionante máximo y tienen el
mismo esfuerzo de flexión máximo si sus
secciones transversales son: 1) un rectángulo
con altura igual a dos veces el ancho; 2) un
cuadrado y 3) un círculo (ver las figuras).
Respuesta: 1.00, 1.26, 1.408
5. G 5.8-lO Una viga de madera simplemente
apoyada de sección transversal rectangular tiene
un claro de 1.2 m y sostiene una carga
concentrada P al centro del claro, además de su
propio peso (véase la figura). La sección
transversal tiene 140 mm de ancho y 240 mm
de alto. La densidad de la madera es igual a 5.4
kN/m3.
Calcule el valor permisible máximo de la carga
P si: a) el esfuerzo de flexión permisible es de
8.5 MPa y b) el esfuerzo cortante permisible es
0.8 MPa. Respuesta: a) P = 38 KN, b) P = 35.6
KN.
6. B 6.10 Para la viga y la carga que se
muestran en la figura, considere la sección n-n
y determine a) el máximo esfuerzo cortante en
dicha sección, b) el esfuerzo cortante en el
punto a.
7. B 6.13 Dos placas de acero con sección
transversal rectangular de 12 x 220 mm se
sueldan a una viga W250 x 58, como se
muestra en la figura (consultar propiedades de
la sección en el apéndice C de Beer). Determine
el cortante vertical máximo permisible si el
esfuerzo cortante en la viga no debe exceder 90
MPa. Respuesta: 177.9 kN.
8. G5.8-12 Una viga de madera ABC con
apoyos simples en A y B y un voladizo BC,
tiene altura h = 280 mm (véase la figura). La
longitud del claro principal de la viga es L = 3.6
m y la longitud del voladizo es L/3 = 1.2 m. La
viga soporta una carga concentrada 3P = 15 kN
en el centro del claro principal y una carga P =
5 kN en el extremo libre del voladizo. La
madera tiene un peso específico γ =
5.5 kN/m3.
a) Determine el ancho b requerido en la viga
con base en un esfuerzo de flexión permisible
de 8.2 MPa.
b) Determine el ancho b requerido con base en
un esfuerzo cortante permisible de 0.7 MPa.
Respuesta: a) b = 99.8 mm, b) b= 71.8 mm.
9. B 6.16 Para la viga de patín ancho que
soporta la carga mostrada en la figura,
determine la máxima carga P que puede
aplicarse. Consultar propiedades de la sección
en el apéndice C de Beer. Considere que el
máximo esfuerzo normal es de 160 MPa y que
el máximo esfuerzo cortante usando la
aproximación τmax = V/Aalma es de 100 MPa.
Respuesta: 178.7 kN
10. B6.92 Para la viga y las cargas que se
muestran en la figura, considere la sección n-n
y determine el esfuerzo cortante en a) el punto
a, b) el punto b. Respuesta: a) 1.313 ksi, b)2.25
ksi.
11. G 9.3-2 Una viga de acero de patín ancho
uniformemente cargada con apoyos simples
(véase la figura) tiene una deflexión hacia abajo
de 10 mm en el centro del claro y ángulos de
rotación iguales a 0.01 radianes en los
extremos.
Calcule el peralte h de la viga si el esfuerzo de
flexión máximo es de 90 MPa y el módulo de
elasticidad es de 200 GPa. Respuesta h= 96
mm.
12. G 9.3-16 Obtenga las ecuaciones de la
curva de deflexión para una viga simple AB
sometida a una carga uniforme de intensidad q
que actúa sobre la mitad izquierda del claro
(véase la figura). Determine también la
deflexión δc en el centro del claro de la viga.
(Nota: use la ecuación diferencial de segundo
orden de la curva de deflexión.) Respuesta: δc =
(5qL4) / (768EI)
13. B 9.48 Para la viga y la carga mostradas en
la figura, (viga S130 x 15, altura 127 mm, Ix =
5.07 x 106 mm4) determine a) la pendiente en el
extremo A, b) la deflexión en el punto medio C.
Utilice E = 200 GPa. Respuesta. a) 5.46 x 10-3
rad, b) 3.09 mm hacia abajo.
14. B 9.55 Para la viga y la carga que se
muestran en la figura, determine a) la reacción
en el punto A, b) la deflexión en el punto C.
Utilice E = 29 x 106 psi. (Viga W 10 x 22,
altura 10.17 in, Ix = 118 in4)
15 B 6.21 y 6.23 Para la viga y las cargas que
se muestran en la figura, considere la sección nn y determine el esfuerzo cortante en a) el punto
a, b) el punto b, c)el esfuerzo cortante máximo
en la sección n-n. Respuesta a) 31 MPa, b) 23.2
MPa, c) 32.7 MPa.