+ R
Anuncio

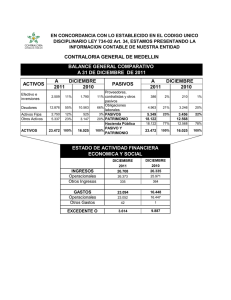
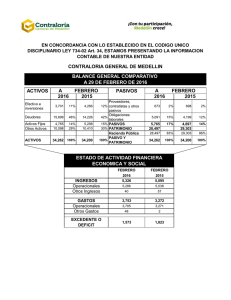
Máster en Mecatrónica EU4M Master in Mechatronic and Micro-Mechatronic Systems CONCEPTOS PREVIOS Fundamentos de Ingeniería Eléctrica Contenidos • Fuentes Tensión y corriente • Elementos pasivos Tipos Asociación Comportamiento en continua • Leyes de Kirchoff Nudos y mallas • Teoremas Superposición Millman Norton y Thèvenin • Resolución de circuitos de primer orden Fuentes. Tensión y corriente Representación de fuentes ideales Tensión + V VDC Corriente Fijan la tensión que hay entre dos puntos Fija la intensidad de corriente que circula por una determinada rama. I Las fuentes reales incorporan una impedancia interna rs + V rs VDC I Rp Elementos pasivos. Tipos Resistencias R i v(t) = R · i(t) i(t) = v(t) R v Condensadores C t i v(t) = 1 ⌠ · i(t) dt C ⌡ i(t) = C · 0 v dv(t) dt Bobinas o inductancias L v i di(t) v(t) = L · dt t i(t) = 1 ⌠ · v(t) dt L ⌡ 0 Elementos pasivos. Asociación Resistencias y bobinas Asociación serie R1 R2 Rn Req ··· Req = R1 + R2 + ··· + Rn Análogo para bobinas Asociación paralelo L1 L2 Leq Leq ··· Ln Para n=2: = L1·L2 / (L1+L2) 1 1 1 1 = + + ··· + Leq L1 L2 Ln Análogo para resistencias Elementos pasivos. Asociación Condensadores Asociación serie C1 C2 ··· Cn 1 1 1 1 = + + ··· + Ceq C1 C2 Cn Asociación paralelo C1 Ceq C2 ··· Cn Ceq Ceq = C1 + C2 + ··· + Cn Elementos pasivos. Comportamiento en DC Cuando las fuentes de un circuito son sólo fuentes de continua, los componentes llegan a comportarse como se indica. R C R DC L Comportamiento en régimen permanente Leyes de Kirchoff. Nudos y mallas Ley de los nudos La suma de corrientes que entran en un nudo es igual a la suma de corrientes que salen del mismo. i1 i2 i1 = i2 + i3 i3 Ley de las mallas La suma de todas las tensiones en una malla (con su signo correspondiente) es siempre nula. ··· ··· v2 v1 ··· v3 ··· v1 - v2 - v3 = 0 La elección de los sentidos de corrientes y tensiones es arbitraria Leyes de Kirchoff. Usando las leyes de Kirchoff, se pueden deducir las expresiones correspondientes a los siguientes divisores resistivos. Divisor de tensión + R1 v1 v1 = V e · R1 R1 + R2 R2 v2 v2 = V e · R2 R1 + R2 Ve Divisor de Corriente i1 Ie R1 i2 i1 = I e · R2 R1 + R2 i2 = I e · R1 R1 + R2 R2 Teoremas. Teorema de superposición La respuesta de cualquier elemento de un circuito lineal que tenga varias fuentes, es la suma de las respuestas individuales obtenida para cada fuente con las demás anuladas. Teorema de Millman Permite calcular la tensión presente en varias ramas formadas por fuente de tensión más resistencia y colocadas en paralelo. ··· R1 R2 + V1 Rn + + V2 Vn ··· Vo Vo = V1 V2 + + ··· + R1 R2 1 1 + + ··· + R2 R1 Vn Rn 1 Rn Teoremas. Teoremas de Norton y de Thèvenin El comportamiento de cualquier circuito lineal de dos salidas puede representarse con un circuito equivalente simplificado consistente en una fuente (de corriente o de tensión) y una resistencia. A Circuito Lineal B A + VTh = (VAB)0 A RTh RTh = RN = VTh / IN VTh B IN = (IAB)cc IN RN B Circuitos de primer orden. Se puede calcular la evolución de las magnitudes eléctricas en circuitos formados por una fuente de continua (tensión o corriente), una resistencia y una bobina o un condensador mediante la siguiente expresión. -t/τ X(t) = X + (X – X )·e X(t) = X∞∞ + (X00 – X∞∞)·e-t/τ X0 X∞ τ Valor inicial de la magnitud a calcular Valor de la magnitud a calcular en régimen permanente Constante de tiempo: τ = R·C ó τ = L/R La evolución de estas magnitudes siempre sigue una exponencial desde el valor inicial hasta el régimen permanente. Se considera que se tarda un tiempo t ≈ 5·τ en llegar al régimen permanente. En régimen permanente los condensadores se comportan como circuitos abiertos y las bobinas, como cortocircuitos. X∞ X0 5·τ