Estimación - Tamaño Muestra
Anuncio

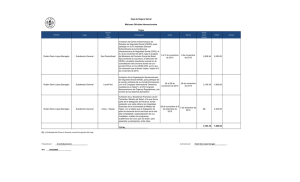
Enero 2016 Ing. Rubén Darío Estrella, MBA Cavaliere dell’ordine al Merito della Repubblica Italiana (2003) Ingeniero de Sistemas (UNIBE 1993), Administrador (PUCMM 2000), Matemático (PUCMM 2007), Teólogo (UNEV 2002) y Maestro (Salomé Uneña 1985) rubendarioestrella@hotmail.com / rubendarioestrellas@gmail.com www.atalayadecristo.org Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Las dos aplicaciones principales de la estadística inferencial implican el uso de datos de muestra para (1) estimar el valor de un parámetro de población y (2) llegar a una conclusión acerca de una población. Estimador: es una estadística de muestra (como la media de muestra) que se usa para aproximar un parámetro de población. Existen dos tipos de estimadores que se utilizan normalmente: - Estimador puntual - Estimador por intervalo Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Estimado puntual: es un valor individual (o punto) que se usa para aproximar un parámetro de población. Estimador Puntual: utiliza un número único o valor para localizar una estimación del parámetro. La media de muestra es el mejor estimado de la media de población. Podemos decir que la media de la muestra es un estimador no predispuesto de la media de la población, lo que quiere decir que la distribución de las medias de muestra tiende a centrarse alrededor del valor de la media de la población. (Es decir, las medias de muestra no tienden a sobreestimar sistemáticamente el valor de , y tampoco tienden a subestimar sistemáticamente dicho valor. En vez de ello, tienden a centrarse en el valor de misma). Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Estimación por intervalo: especifica el rango dentro del cual está el parámetro desconocido. Intervalo de Confianza: denota un rango dentro del cual puede encontrarse el parámetro. Es una gama (o un intervalo) de valores que probablemente contiene el valor verdadero del parámetro de población. Un intervalo de confianza se asocia a un grado de confianza, que es una medida de la certeza que tenemos de que nuestro intervalo contiene el parámetro de población. Nivel de confianza (grado o coeficiente de confianza): es la probabilidad 1- (a menudo expresada como el valor porcentual equivalente) de que el intervalo de confianza contiene el verdadero valor del parámetro. Existen tres niveles de confianza relacionados comúnmente con los intervalos de confianza: 99, 95 y 90%, denominados coeficientes de confianza. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Valor Alfa : Es la probabilidad de error o la probabilidad de que un intervalo dado no contenga la media poblacional desconocida. Valor Critico Z: Es el número que está en la frontera que separa las estadísticas de muestra que probablemente ocurrirán, de aquellas que probablemente no ocurrirán. Es un puntaje con la propiedad de que separa un área de /2 de la cola derecha de la distribución normal estándar. Margen de Error E: Es la máxima diferencia probable (con una probabilidad de 1-) entre la media de muestra observada y el verdadero valor de la media de población . El margen de error también se denomina error máximo de la estimación y puede obtenerse multiplicando el valor critico y la desviación estándar de las medias de muestras. E = Z * /n Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 E = Z * /n Intervalo de confianza para estimar (media poblacional real desconocida) cuando es conocida. I. C. para estimar = X' E Caso I. Para estimar el gasto promedio de los clientes en el McDonald's local, los estudiantes de Métodos Cuantitativos toman una muestra de 200 clientes y encuentran un gasto promedio de US$5.67, con una desviación estándar poblacional de US$1.10. ¿Cuál es el intervalo de confianza del 95% para los gastos promedio de todos los clientes? Interprete sus resultados. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Caso I. Para estimar el gasto promedio de los clientes en el McDonald's local, los estudiantes de Métodos Cuantitativos toman una muestra de 200 clientes y encuentran un gasto promedio de US$5.67, con una desviación estándar poblacional de US$1.10. ¿Cuál es el intervalo de confianza del 95% para los gastos promedio de todos los clientes? Interprete sus resultados. I. C. para estimar = X' E Datos: E = Z * /n = 1.96 * (1.10/200) = 0.15 n=200 I.C. para estimar = US$5.67 0.15 N.C.=95% x'=US$5.67 I.C.=? σ=US$1.10 = US$5.52 US$5.82 Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 MEGASTAT Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 MEGASTAT Confidence interval - mean 95% confidence level 5.67 mean 1.1 std. dev. 200 n 1.960 z 0.152 half-width 5.822 upper confidence limit 5.518 lower confidence limit Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Caso I. Para estimar el gasto promedio de los clientes en el McDonald's local, los estudiantes de Métodos Cuantitativos toman una muestra de 200 clientes y encuentran un gasto promedio de US$5.67, con una desviación estándar poblacional de US$1.10. ¿Cuál es el intervalo de confianza del 95% para los gastos promedio de todos los clientes? Interprete sus resultados. I. C. para estimar = X' E E = Z * /n = 1.96 * (1.10/200) = 0.15 I. C. = US$5.52 US$5.82 Los estudiantes poseen un 95% de confianza de que la media poblacional desconocida del gasto de los clientes del McDonal's evaluados se encuentra entre el intervalo US$5.52 US$5.82. Si se construyen todos los NCn intervalos de confianza, el 95% de ellos contendrá la media poblacional desconocida. Esto por supuesto significa que el 5% de todos los intervalos estaría errado no contendrían la media poblacional, el Valor alfa . Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Si n > 30, podemos sustituir de la formula del E por la desviación estándar de la muestra s. E = Z * s/n Procedimiento para construir un intervalo de confianza para (basado en una muestra grande: n > 30). 1. Encuentre el valor critico Z que corresponda al grado de confianza deseado. 2. Evalúe el margen de error E = Z * /n. Si se desconoce la desviación estándar de la población , use el valor de la desviación estándar de la muestra s, siempre que n > 30. 3. Con el valor del margen de error calculado y el valor de la media de muestra X', obtenga los valores de X'-E y X'+E. Sustituya estos valores en el formato general del intervalo de confianza: X'-E X'+E = X' E (X'-E ,X'+E 4. Redondee los valores resultantes aplicando la regla de redondeo. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 1. Si usa el conjunto de datos original para construir un intervalo de confianza, redondee los limites del intervalo de confianza a una posición decimal más que las empleadas en el conjunto de datos original. 2. Si desconoce el conjunto de datos original y sólo usa las estadísticas resumidas (n, x', s), redondee los limites del intervalo de confianza de acuerdo al mismo número de posiciones decimales que se usan para la media de muestra. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Justificación: La idea básica en que se apoya la construcción de intervalos de confianza tiene que ver con el teorema del limite central, que indica que en el caso de muestras grandes (n > 30), la distribución de las medias de muestra es aproximadamente normal con media y desviación estándar /n. El formato de los intervalos de confianza en realidad es una variación de la ecuación: Z = (X' - )/(/n) X' - = Z (/n) - = Z (/n) - X' (-1) = X' - Z (/n) = X' E Precisión: Un intervalo estrecho ofrece mayor precisión, aunque la probabilidad de que contenga se reduce. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Caso I. Una muestra consiste en 75 televisores adquiridos hace varios años. Los tiempos de reemplazo de esos televisores tienen una media de 8.2 años y una desviación estándar de 1.1 años (basados en datos de "Getting Things Fixed", Consumer Reports). Construya un intervalo de confianza del 90% para el tiempo de reemplazo medio de todos los televisores de esa época. Caso II. Utilice el grado de confianza y los datos de muestra dados para determinar (a) el margen de error y (b) el intervalo de confianza para la media de la población 1. Estaturas de mujeres: confianza del 95%; n=50, x'=63.4 pulgs., s=2.4 pulgs. 2. Promedios de calificaciones: confianza del 99%; n=75, x'=2.76, s=0.88. 3. Puntajes en una prueba: confianza del 90%; n=150, x'=77.6; s=14.2. Ejercicios de la Sección 1 al 10 págs. 175 y 176. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Las decisiones dependen con frecuencia de parámetros que son binarios, parámetros con sólo dos posibles categorías dentro de las cuales pueden clasificarse las respuestas. En este evento, el parámetro de interés es la proporción poblacional. Tanto las proporciones como las probabilidades se expresan en forma decimal o fraccionaria. Al trabajar con porcentajes, los convertimos en proporciones omitiendo el signo de por ciento y dividiendo entre 100. Por ejemplo, la tasa del 48% de personas que no compran libros puede expresarse en forma decimal como 0.48. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Estimado puntual para la proporción de población. La proporción de muestra p es el mejor estimado puntual de la proporción de población. p = x/n proporción de muestra de x éxitos en una muestra de tamaño n. Intervalo de confianza para la proporción poblacional. Muchos asuntos de negocios tratan la proporción de la población. Una firma de marketing puede querer averiguar si un cliente (1) compra o (2) no compra el producto. Un banco con frecuencia debe determinar si un depositante (1) pedirá o (2) no pedirá un crédito para auto. Muchas firmas deben determinar la probabilidad de que un proyecto para presupuestar capital (1) generará o (2) no generará un rendimiento positivo. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Si n*p y n*(1-p) son mayores que 5, la distribución de las proporciones muestrales será normal y la distribución muestral de la proporción muestral tendrá una media igual a la proporción poblacional y error estándar de: Error estandar de la distribución muestral de las proporciones muestrales: ________ ____ p = p(1-p)/n = pq/n Estimación del Error estándar de la distribución muestral de las proporciones muestrales: _________ _____ sp = p(1-p)/n = pq/n Margen de error del estimado de la proporción de la población: ______ E = (Z)( pq/n) Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Regla de redondeo para estimados de intervalo de confianza para la proporción de población Redondee los limites del intervalo de confianza a tres dígitos significativos. Intervalo de confianza para estimar la proporción poblacional. I.C. para estimar la proporción poblacional = p E Caso I. E = (Z)( pq/n) En una encuesta de 1068 estadounidenses, 673 dijeron que tenían contestadoras telefónicas (basados en datos de International Mass Retail Association, informados en USA Today). Utilizando estos resultados de muestra, determine: a. El estimado puntual de la proporción de la población de todos los estadounidenses que tienen contestadora telefónica. b. El estimado de intervalo del 95% de la proporción de todos los estadounidenses que tienen contestadora telefónica. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 I.C. para estimar la proporción poblacional =pE Caso I. E = (Z)( pq/n) En una encuesta de 1068 estadounidenses, 673 dijeron que tenían contestadoras telefónicas (basados en datos de International Mass Retail Association, informados en USA Today). Utilizando estos resultados de muestra, determine: a. El estimado puntual de la proporción de la población de todos los estadounidenses que tienen contestadora telefónica. b. El estimado de intervalo del 95% de la proporción de todos los estadounidenses que tienen contestadora telefónica. a. Estimado puntual para la proporción de población. p = x/n = 673/1068 = 0.630 b. Intervalo de confianza para estimar la proporción poblacional. E = 1.96 ((0.630)(0.370)/1068) = 0.0290 I.C. para estimar la proporción poblacional: 0.630 - 0.0290 < < 0.630 + 0.0290 0.601 < < 0.659 Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 MEGASTAT Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 MEGASTAT Confidence interval - proportion 95% confidence level 0.63 proportion 1068 n 1.960 z 0.029 half-width 0.659 upper confidence limit 0.601 lower confidence limit Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 En una encuesta de 1068 estadounidenses, 673 dijeron que tenían contestadoras telefónicas (basados en datos de International Mass Retail Association, informados en USA Today). Utilizando estos resultados de muestra, determine: a. El estimado puntual de la proporción de la población de todos los estadounidenses que tienen contestadora telefónica. b. El estimado de intervalo del 95% de la proporción de todos los estadounidenses que tienen contestadora telefónica. a. Estimado puntual para la proporción de población. p = x/n = 673/1068 = 0.630 b. Intervalo de confianza para estimar la proporción poblacional. E = 1.96 (((0.630*0.370)/1068)) = 0.0290 I.C. para estimar la proporción poblacional: 0.630 - 0.0290 < < 0.630 + 0.0290 0.601 < < 0.659 Este resultado a menudo se informa en el formato siguiente: "Se estima que el porcentaje de los estadounidenses que tiene contestadora telefonica es del 63%, con un margen de error de mas o menos 2.9 puntos porcentuales. También debe informarse el nivel de confianza, pero eso casi nunca se hace en los medios de comunicación. EJERCICIOS DE LA SECCION 20 AL 25 - PAG. 182. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Los factores como el costo y el tiempo a menudo limitan severamente el tamaño de las muestras, y es posible que la distribución normal no sea una aproximación adecuada a la distribución de las medias de muestras pequeñas. En muestras pequeñas, la media de muestra X' generalmente es el mejor estimado puntual de la media de la población . Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Condiciones para usar la Distribución t de Student. La muestra es pequeña (n 30). Se desconoce . La población padre tiene una distribución esencialmente normal. (Dado que a menudo se desconoce la distribución de la población padre, la estimamos construyendo un histograma con datos de muestra.) Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Propiedades importantes de la Distribución t de Student: 1.- La distribución t de Student es diferente para los diferentes tamaños de muestra. (Ver Figura 7.3 en la Pág. 177). 2.- La distribución t de Student tiene la misma forma general de campana simétrica que la distribución normal estándar, pero refleja la mayor variabilidad (con distribuciones más amplias) que cabe esperar cuando la muestra es pequeña. 3.- La distribución t de Student tiene una media t=0 (así como la distribución normal estándar tiene una media de Z=0). Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 4.- La desviación estándar de la distribución t de Student varia con el tamaño de la muestra, pero es mayor que 1 (a diferencia de la distribución normal estándar, que tiene =1). Al igual que la distribución Z, la distribución t tiene una media de cero, es simétrica respeto a la media y oscila entre - y + . Sin embargo, mientras que la distribución Z tiene una varianza de ²=1, la varianza de la distribución t es mayor que 1. 5.- A medida que aumenta el tamaño de muestra n, la distribución t de Student se acerca mas a la distribución normal estándar. Con valores de n > 30, las diferencias son tan pequeñas que podemos utilizar los valores críticos de z en lugar de crear una tabla mucho más grande de valores críticos de t. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Varianza de la distribución t ² = (n-1)/(n-3) La varianza depende de los grados de libertad (g.l.), que definimos como el número de observaciones que se pueden escoger libremente. Es el número de observaciones menos el número de restricciones impuestas sobre las observaciones, en donde una restricción es algún valor que tales observaciones deben poseer. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Grados de Libertad: El número de grados de libertad de un conjunto de datos corresponde al número de puntajes que puede variar después de haber impuestos ciertas restricciones a todos los puntajes. Es el número de observaciones menos el número de restricciones impuestas sobre tales observaciones. g.l. = n - 1 Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 El estadístico t t = (X'-) / (s / n) Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Margen de Error para la Estimación de : E = t * s/n Intervalo de Confianza para la estimación de (Basada en una muestra pequeña (n 30) y desconocida) I. C. para estimar = X' E X' - E < < X' + E Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Caso I. Cuando se usan pruebas destructivas, los elementos de una muestra se destruyen durante el proceso de probarlos. Las pruebas de choques de automóviles son un ejemplo muy costoso de pruebas destructivas. Si usted estuviera encargado de tales pruebas de choque, no querría decirle a su supervisor que necesita chocar y destruir mas de 30 automóviles para poder usar la distribución normal. Supongamos que usted ha probado 12 automóviles deportivos Dodge Viper (Precio d lista actual: US$59,300 dólares) chocándolos en diversas condiciones que simulan colisiones representativas. Un análisis de los 12 automóviles dañados da como resultado costos de reparación cuya distribución al parecer tiene forma de campana, con una media de X'=US$26,227 y una desviación estándar de s=$15,873 (basado en datos de Highway Loss Data Institute). Determine lo siguiente. a) El mejor estimado puntual de la media de población , el costo de reparación medio de todos los Dodge Viper implicados en colisiones. b) El estimado de intervalo del 95% de , el costo de reparación medio de todos los Dodge Viper implicados en colisiones. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Solución: a) El mejor estimado puntual de la media de población es el valor de la media de muestra X'. En este caso, entonces, el mejor estimado puntual de es US$26,227 dólares. b) DATOS: n = 12 automóviles deportivos Dodge Viper X'=US$26,227 dólares costo de reparación s =US$15,873 dolares N.F.= 95% ===> t= ? I.C. para = ? Dada las condiciones anteriores: 1.- La muestra es pequeña (n30). 2.- Se desconoce . 3.- La población padre tiene una distribución esencialmente normal. (Dado que a menudo se desconoce la distribución de la población padre, la estimamos construyendo un histograma con datos de muestra.) podemos usar la Distribución t de Student: Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 g.l. = grados de libertad = g.l. = n-1 = 12-1 = 11 usando la tabla de la distribución t (Pág. 606) con los g.l.=11 y N.C.=95% cuyas colas equivalen a 5% (0.05) determinamos el valor critico t. g.l.=11; I.C. con N.C.=95% (0.950); dos colas=5% (0.050) ==> t=2.201 donde E = t (s/n) E = 2.201 (15,873/12) = US$10,085.29 El intervalo de confianza es: X' - E < < X' + E US$26,227-US$10,085.29< < US$26,227+US$10,085.29 US$16,142 < < US$36,312 [Este resultado también podría expresarse en el formato de =US$26,227US$10,085.29 o como (US$16,142, US$36,312).] Con base en los resultados de muestra dados, tenemos un 95% de confianza en que los limites de USD16,142 y USD36,312 contendrán realmente el valor de la media de población . Estos costos de reparación parecen muy altos. Efectivamente, el Dodge Viper es actualmente el automóvil más costoso de reparar después de una colisión. Tal información es importante para compañías que aseguran Dodge Vipers contra choques. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Confidence interval - mean 95% confidence level 26227 mean 15873 std. dev. 12 n 2.201 t (df = 11) 10085.223 half-width 36312.223 upper confidence limit 16141.777 lower confidence limit Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 122 Caso II. Utilice el grado de confianza y los datos de muestra dados para determinar (a) el margen de error y (b) el intervalo de confianza para la media de la población . 1) Estaturas de mujeres: confianza del 95%; n=10, x'=63.4 pulg., s=2.4 pulg. 2) Promedios de calificaciones: confianza del 99%; n=15, x'=2.76, s=0.88 3) Puntajes en una prueba: confianza del 90%; n=16, x'=77.6, s=14.2 4) Salarios de policías: confianza del 92%; n=19, x'=$23,228, s=$8,779 Caso III. Ejercicios 12 al 18 Págs. 179-180 y Analizar figura 7.4 Pág. 179. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 El tamaño de la muestra juega un papel importante al determinar la probabilidad de error así como en la precisión de la estimación. Una vez se ha seleccionado el nivel de confianza, los factores importantes influyen en el tamaño muestral: (1) la varianza de la población ² y (2) el tamaño del error E tolerable investigador esta dispuesto a aceptar. que el Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Tamaño de la muestra para estimar . Z = (X' - )/(/n) X' - = Z (/n) n(X' - ) = Z n = Z/(X' - ) n = Z²²/(X' - )² n = Z²²/E² n =[Z/E]² E = Error de Muestreo El tamaño de la muestra debe ser entero. Regla de redondeo para el tamaño de muestra n. Al calcular el tamaño de muestra n, si la fórmula anterior no produce un número entero, siempre debe aumentarse el valor de n al siguiente numero entero mayor. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 n =[Z/E]² El tamaño de la muestra no depende del tamaño de la población (N); el tamaño de muestra depende del grado de confianza deseado, el margen de error deseado y del valor de la desviación estándar . La duplicación del margen de error hace que el tamaño de la muestra requerida se reduzca a la cuarta parte de su valor original. Por otro lado, si se reduce a la mitad el margen de error se cuadruplicará el tamaño de la muestra. Lo que esto implica es que si queremos resultados más exactos, es preciso aumentar sustancialmente el tamaño de la muestra. Dado que las muestras grandes generalmente requieren más tiempo y dinero, a menudo es necesario efectuar un trueque entre el tamaño de la muestra y el margen de error E. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 n =[Z/E]² Caso I. Un economista desea estimar los ingresos medios durante el primer año de trabajo de un graduado universitario que, en un alarde de sabiduría, tomo un curso de estadística. ¿Cuantos de tales ingresos es necesario encontrar si queremos tener una confianza del 95% en que la media de muestra este a menos de US$500 dólares de la verdadera media de la población? Suponga que un estudio previo revelo que, para tales ingresos, = US$6250. DATOS: N.C.=95% ===> Z=1.96 Queremos que la media de la muestra este dentro de un margen de US$500 de la media de la población. E=US$500 =US$6,250 n = [(1.96 * 6250)/500]²= Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 MEGASTAT Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Caso II. ¿Que tan grande se requiere que sea una muestra para que proporcione una estimación del 90% del numero promedio de graduados de las universidades de la nación con un error de 2000 estudiantes si una muestra piloto reporta que s=8,659? Caso III. Nielsen Media Research quiere estimar la cantidad media de tiempo (en horas) que los estudiantes universitarios de tiempo completo dedican a ver televisión cada día entre semana. Determine el tamaño de muestra necesario para estimar esa media con un margen de error de 0.25 horas (15 minutos). Suponga que se desea un grado de confianza del 96%, y que un estudio piloto indico que la desviación estándar se estima en 1.87 horas. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 ¿QUE PASA SI SE DESCONOCE ? 1.- Podemos utilizar la REGLA PRACTICA DE INTERVALO. En conjuntos de datos representativos, el intervalo del conjunto tiene una anchura aproximada de cuatro desviaciones estándar (4s), así que la desviación estándar se puede aproximar de la siguiente manera: desviación estándar intervalo/4 intervalo/4 Esta expresión proporciona una estimación burda de la desviación estándar, si conocemos los puntajes máximo y mínimo. Si conocemos el valor de la desviación estándar, podemos usarlo para entender mejor los datos, obteniendo estimaciones burdas de los puntajes máximo y mínimo como se indica. mínimo (media) - 2 * (desviación estándar) máximo (media) + 2 * (desviación estándar) Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 ¿QUE PASA SI SE DESCONOCE ? Caso I. n =[Z/E]² Si razonamos que los precios de los libros de textos universitario típicamente varían entre US$10 y US$90 dólares. Usted planea estimar el precio de venta medio de un libro de texto universitario. ¿Cuantos libros de textos deberá muestrear si desea tener una confianza del 95% en que la media de la muestra estará a menos de US$2 dólares de la verdadera media de la población ? DATOS: intervalo/4 (US$90-US$10)/4 US$20 N.C.=95% ===> Z=1.96 E=US$2 dólares Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 ¿QUE PASA SI SE DESCONOCE ? n =[Z/E]² Caso II. Boston Marketing Company lo acaba de contratar para realizar una encuesta con el fin de estimar la cantidad media de dinero que los asistentes al cine de Massachussets gastan (por película). Primero use la regla practica del intervalo para hacer un estimado burdo de la desviación estándar de las cantidades gastadas. Es razonable suponer que las cantidades típicas varían entre US$3 dólares y unos US$15 dólares. Luego utilice esa desviación estándar para determinar el tamaño de muestra que corresponde a una confianza del 98% y a un margen de error de 25 centavos de dólar. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Si despejamos a "n" de la expresión del margen de error E. E = (Z) (pq/n) E² = (Z)²(pq/n)² E² = (Z)²(pq/n) E²n = (Z)²(pq) n = [(Z)²(pq)]/E² Cuando se puede obtener un estimado razonable de p utilizando muestras previas, un estudio piloto o los conocimientos de algún experto se utiliza la formula anterior. Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Cuando no se conoce el estimado puntual p: n = [(Z)²* 0.25]/E² Si no se puede conjeturarse un valor, puede asignarse el valor de 0.5 tanto a p como a q, con lo que el tamaño de muestra resultante será al menos tan grande como necesita ser. La justificación para la asignación de 0.5 es la siguiente: el valor mas alto posible del producto p*q es de 0.25, y ocurre cuando p=0.5 y q=0.5 como se puede observar en la siguiente tabla que usted debe completar: p q p*q 0.1 0.9 0.09 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Caso I. Las compañías de seguros se están preocupando porque el creciente uso de teléfonos celulares esta teniendo como resultado un mayor número de accidentes automovilísticos, y están considerando implementar tarifas más altas para conductores que usan tales aparatos. Queremos estimar, con un margen de error de tres puntos porcentuales, el porcentaje de conductores que hablan por teléfono mientras conducen. Suponiendo que queremos tener una confianza del 95% en nuestros resultados, ¿cuántos conductores deberán encuestar? a. Supongamos que tenemos un estimado de p basado en un estudio previo que indicó que el 18% de los conductores habla por teléfono (basados en datos de la revista Prevention). b. Suponga que no tenemos información previa que sugiera un posible valor de p. SOLUCION: a) DATOS: n = [(Z)²(pq)]/E² p=0.18 ; q=0.82 n = [(1.96)²(0.18*0.82]/(0.03)² = N.F.=95% ==> Z=1.96 E=0.03 = tres puntos porcentuales b) DATOS: n = [(Z)²* 0.25]/E² n = [(1.96)²* 0.25]/(0.03)² = Estimados y Tamaño de Muestra ESTRELLA, Rubén Darío. Modelos Estadísticos para la Toma de Decisiones. Edición 2016. Pág. 110 Caso II. Una compañía de comunicaciones esta considerando un proyecto para prestar servicio telefónico de larga distancia. Se le pide a usted realizar un sondeo de opinión para estimar el porcentaje de los consumidores que esta satisfecho con su servicio telefónico de larga distancia actual. Usted quiere tener una confianza del 90% en que su porcentaje de muestra estará a menos de 2.5 puntos porcentuales del valor real para la población, y un sondeo sugiere que el porcentaje en cuestión anda alrededor del 85%. ¿Que tan grande deberá ser la muestra?