MOVIMIENTO ARMÓNICO SIMPLE

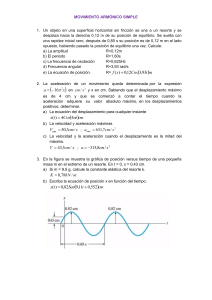
MOVIMIENTO ARMÓNICO SIMPLE
1. Un objeto en una superficie horizontal sin fricción se une a un resorte y se
desplaza hacia la derecha 0,12 m de su posición de equilibrio. Se suelta con
una rapidez inicial cero, después de 0,80 s su posición es de 0,12 m en el lado
opuesto, habiendo pasado la posición de equilibrio una vez. Calcule:
a) La amplitud
R=0,12m
b) El periodo
R=1,60s
c) La frecuencia de oscilación
R=0,625Hz
d) Frecuencia angular
R=3,93 rad/s
e) La ecuación de posición.
R= f ( x)  0,12Cos3,93t m
2. La aceleración de un movimiento queda determinada por la expresión


a   16 2 x en cm / s 2 y x en cm. Sabiendo que el desplazamiento máximo
es de 4 cm y que se comenzó a contar el tiempo cuando la
aceleración adquiere su valor absoluto máximo, en los desplazamientos
positivos, determinar.
a) La ecuación del desplazamiento para cualquier instante
x(t )  4Cos4t cm
b) La velocidad y aceleración máximas
Vmax  50,3cm / s ; amax  631,7cm / s 2
c) La velocidad y la aceleración cuando el desplazamiento es la mitad del
máximo.
V  43,5cm / s ; a  315,8cm / s 2
3. En la figura se muestra la gráfica de posición versus tiempo de una pequeña
masa m en el extremo de un resorte. En t = 0, x = 0,43 cm.
a) Si m = 9,5 g, calcule la constante elástica del resorte k.
K  0,788 N / m
b) Escriba la ecuación de posición x en función del tiempo.
x(t )  0,82Sen9,11t  0,552cm
4. Una partícula oscila con M.A.S. obedeciendo a la ecuación:


x(t )  10 2 Cos 8t  m
6

Donde x se mide en metros y t en segundos.
a) Realice la representación gráfica de x=x(t)
b) Calcule el tiempo que tarda la partícula en pasar por tercera vez por la
posición de equilibrio.
t
7
s
24
c) Calcule la distancia que recorre la partícula en ese tiempo.
d total  4,866cm
5. Un bloque de 5,00 kg que descansa en una superficie horizontal sin fricción
está conectada a un resorte en equilibrio de constante elástica k = 120 N/m,
determine la ecuación de posición del bloque en las siguientes situaciones:
a) Si la masa recibe inicialmente un empujón rápido (4,90 m/s) que comprime
el resorte.


x(t )  1Cos 4,90t  m
2

b) Si se comprime el resorte 4,0 m y luego se suelta.
x(t )  4Cos4,90t   m
6. Un Bloque P ejecuta movimiento armónico simple horizontal cuando se desliza
por una superficie sin fricción con una frecuencia de 1,50Hz. El bloque B se
apoya sobre el primero y el coeficiente de fricción estática entre los dos es de
  0,6
¿Qué amplitud máxima de oscilación puede tener el sistema si el bloque B no
debe resbalar?
A=6,63cm
7. Un cuerpo que desarrolla un M.A.S. en la horizontal, se encuentra inicialmente
a la derecha de su posición de equilibrio moviéndose a la izquierda, donde
además su energía cinética y potencial son iguales. Si luego de transcurrido
0,5s su rapidez es de 2π m/s, y durante una oscilación completa la energía
cinética es mayor que la energía potencial durante 2s; determine la ecuación
de su movimiento.
5 

x(t )  4 Sen t 
m
4 
2
8. En una M.A.S. la amplitud de las oscilaciones es A, con un periodo de 18s.
Determine el intervalo de tiempo mínimo que emplea la partícula en ir desde

x

A
A
hasta x  
2
2
Rspt=3s
9. Un bloque de 4kg, se encuentra en reposo. De pronto se desplaza hacia la
izquierda y luego es soltado. Determine la ecuación de su movimiento, si en
cada oscilación el bloque recorre 100cm
3

x(t )  25Sen 5t 
2


cm

10. Un resorte de constante elástica K=10N/m y longitud natural L0  1m ; se
sostiene del techo por uno de sus extremos, y está suspendido verticalmente.
Si un bloque de masa m=0,5Kg se cuelga suavemente del extremo libre del
resorte y luego se suelta, determine su la amplitud y la frecuencia angular.
A  0,5m ;   2 5rad / s