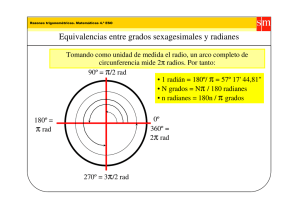
Guía de trabajo autónomo El trabajo autónomo es la capacidad de realizar tareas por nosotros mismos, sin necesidad .de que nuestros/as docentes estén presentes GTA 2 II SEMESTRE 2020 Centro Educativo: Liceo Laboratorio Emma Gamboa Educadora: Paola Guevara Ulloa Nivel: Noveno Asignatura: Matemáticas. Fecha de entrega al estudiante: Del 10 al 14 de agosto Fecha de devolución al profesor: Del 17 al 21 de agosto 1. Me preparo para hacer la guía Pautas que debo verificar antes de iniciar mi trabajo. Materiales o recursos que voy a necesitar Cuaderno de matemática, hojas adicionales, lápiz, lapicero y borrador. Puede utilizar calculadora sencilla. Buena iluminación, mesa con silla o un lugar donde pueda Condiciones que debe tener el lugar donde voy a apoyar el cuaderno cómodamente, buena ventilación. trabajar Tiempo en que se espera que realice la guía 60 minutos. Voy a recordar lo aprendido en clase. Indicaciones Se presentan en esta sección algunos de los conocimientos matemáticos correspondiste al tema de trigonometría del primer periodo para sétimo año, del programa de matemática. Se pretende que cada estudiante, analice la materia, observe videos y haga consultas a la docente si tiene dudas y realice los ejercicios propuestos. https://www.youtube.com/watch?v=seR9VVW4DaI https://www.youtube.com/watch?v=nKSylFrOzRw Ver cada video con atención, luego intente realizar independientemente los ejercicios que se indican en ellos con el fin de evacuar dudas y, por último, Realizar los ejercicios que se le proponen en la guía de trabajo autónomo. Para los estudiantes que NO CUENTAN con dispositivos móviles e internet para acceder a los enlaces anteriores, se les brinda la información necesaria para refrescar conocimientos. Introducción Actividad Sabes que hay diferentes unidades de medida para medir la misma cosa. Por ejemplo, la longitud se puede medir en pies y metros y la temperatura se puede medir en grados Centígrados y grados Fahrenheit. Normalmente usamos fórmulas para convertir entre distintas unidades de medida. También hay dos maneras de medir ángulos. Sabes cómo medirlos en grados. Ahora aprenderás a medirlos en radianes y cómo convertir entre éstas unidades de medida. Mientras que los grados se usan en las actividades diarias como en la construcción y la topografía, la medida en radianes se usa para muchos cálculos, como la velocidad y distancia de los satélites alrededor de la Tierra — ¡incluyendo la Estación Espacial Internacional! Es importante poder medir ángulos en radianes, así como en grados para poder convertir entre los dos sistemas. ¿Qué es un ángulo central? Para poder definir los radianes, es necesario introducir el concepto de ángulo central. Un ángulo central es un ángulo cuyo vértice está en el centro de un círculo. En el círculo siguiente, el centro es el punto O, la longitud del radio es r, y es el ángulo central. Observa que determina un arco con longitud s. La medida en radianes del ángulo central, normalmente denotada por la letra Griega teta ( ), se define como la razón de la longitud del arco y la longitud del radio. Entonces la medida en radianes de está dada por: ¿Qué es un radián? El radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia que subtiende un arco cuya longitud es igual a la del radio. Su símbolo es rad. Usaremos esto para convertir de grados a radianes y vice versa. Si bien los grados siempre se escriben con el símbolo (°), los radianes normalmente se escriben sin ningún símbolo o unidad. Preguntas para reflexionar y responder Al finalizar esta guía de trabajo el estudiante debe poder responder a preguntas como: 1) ¿Qué es un radian? 2) ¿Cuál es el factor para convertir de radianes a grados? 2. Pongo en práctica lo aprendido. Indicaciones Se le presentan una serie de ejercicios y problemas que pretenden reforzar su aprendizaje. El error es parte del aprendizaje, si no puede resolver algún ejercicio o surgen dudas no dude en consultar con la docente, a través de los medios antes citados. Trabaje en orden, con paciencia y entusiasmo por adquirir o reforzar los aprendizajes. Indicaciones o preguntas para auto regularse y evaluarse Para reflexionar sobre lo realizado, haga las siguientes preguntas: ¿Qué sabía antes de estos temas y qué sé ahora? ¿Qué puedo mejorar de mi trabajo? ¿Cómo le puedo explicar a otra persona lo que aprendí? ¿En qué áreas se pueden aplicar estos conocimientos? Práctica Convierta de grados a radianes o viceversa los siguientes ángulos 180º= 200º= 155º = 430º= 300º= 330º= 78º= 86º= 60º= Estudiante Con el trabajo autónomo voy a aprender a aprender Reviso las acciones realizadas durante la construcción del trabajo. Marco una X encima de cada símbolo al responder las siguientes preguntas ¿Leí las indicaciones con detenimiento? ¿Subrayé las palabras que no conocía? ¿Busqué en el diccionario o consulté con un familiar el significado de las palabras que no conocía? ¿Me devolví a leer las indicaciones cuando no comprendí qué hacer? Con el trabajo autónomo voy a aprender a aprender Valoro lo realizado al terminar por completo el trabajo. Marca una X encima de cada símbolo al responder las siguientes preguntas ¿Leí mi trabajo para saber si es comprensible lo escrito o realizado? ¿Revisé mi trabajo para asegurarme si todo lo solicitado fue realizado? ¿Me siento satisfecho con el trabajo que realicé? Explico ¿Cuál fue la parte favorita del trabajo? ¿Qué puedo mejorar, la próxima vez que realice la guía de trabajo autónomo? AUTOEVALUACIÓN Habilidad: Convertir medidas angulares de grados a radianes y viceversa. Marco con una equis dentro del paréntesis que más se acerca a mi nivel de desempeño al realizar la guía de trabajo autónomo. Indicador (Pautas para el desarrollo de la habilidad) Causalidad entre componentes sistema Indicadores del aprendizaje esperado los Descubre del relaciones entre diferentes medidas angulares. Inicial ( ) Proceso Intermedio ( ) Cito la diferencia Determino las entre medidas relaciones entre angulares en grados y radianes. grados y en radianes. Avanzado ( ) Realizo conversiones de medidas angulares a radianes y viceversa.