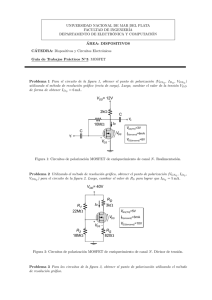
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
1
Taller del laboratorio No. 4
CARACTERIZACIÓN Y AMPLIFICACIÓN CON
TRANSISTORES MOSFET
Johan Alejandro López Arias, johalopezari@unal.edu.co
Electrónica Análoga
Departamento de Ingeniería Mecánica y Mecatrónica
Universidad Nacional de Colombia.
Bogotá. Colombia.
I Marco teórico
I-A TRANSISTOR MOSFET:
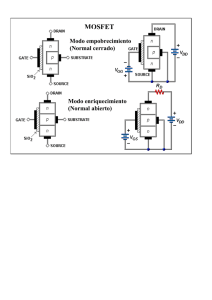
El MOSFET es un transistor con 3 terminales, gate (G),
source (S) y drain (D).
VDD Es la tensión que se ingresa a drain.
VSS Es la tensión que esta en source.
VDS Es la tensión entre drain y source.
Vt Voltaje mínimo necesitado para permitir conducción entre soruce y gate.
La figura 1 muestra las curvas de I D vs VDS para distintos
valores de VGS , esta gráfica permite observar dos regiones
de operación del transistor BSS138. La primera región es
la región triodo que se observa en todas las curvas, y
la segunda región es la región de saturación que solo se
observa para las curvas cuyo valor VGS es 2V, 2.5V y 3v,
correspondiendo esta región a la parte plana de la curva.
I-C Transistor 2N7000.
I-C1 Condiciones de VT N
I-B Transistor BSS138.
VGS t h
VGS t h
Coditions
Min
Typ
Max
Unit
VDS = VGS
I D = 1mA
0.8
2.1
3
V
Tabla I: Valores de VT N para el transistor BSS138.
La tabla anterior contiene la tensión VT N a la cual puede
llegar a operar el transistor BSS138, se observa que el
mínimo valor al que puede operar es a 0.8V con valor
promedio o típico de 2.1V. Esto cuando VDS y VGS son
iguales y operando a una corriente de 1mA.
Coditions
Min
Typ
Max
Unit
VDS = VGS
I D = 1mA
0.8
1.3
1.5
V
Tabla II: Valores de VT N para el transistor 1N7000.
La tabla anterior contiene la tensión VT N a la cual puede
llegar a operar el transistor 2N7000, se observa que el
mínimo valor al que puede operar es a 0.8V con valor
promedio o típico de 2.1V. Esto cuando VDS y VGS son
iguales y operando a una corriente de 1mA.
Figura 2: Curva I D vs VDS para distintos valores de VGS en el transistor 2N7000.
Figura 1: Curva I D vs VDS para distintos valores de VGS en el transistor BSS138.
La figura 1 muestra las curvas de I D vs VDS para distintos
valores de VGS , esta gráfica permite observar dos regiones
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
de operación del transistor 2N7000. La primera región es
la región triodo que se observa en todas las curvas, y
la segunda región es la región de saturación que solo se
observa para las curvas cuyo valor VGS es 3V, 4V,5V y 6V,
correspondiendo esta región a la parte plana de la curva.
2
puesto que la gráfica es una función de transferencia .Así
se tiene el circuito visto en la siguiente figura:
I-C2 Condiciones en Saturación
Coditions
Min
Typ
Max
Unit
VGS = 4.5V,
VDS = 10V
75
600
0
mA
Tabla III: ON-State Drain Current
La tabla III contiene la información de la región de
saturación del transistor 2N7000 para un valor definido de
VGS y VDS .
II Simulaciones.
II-A Simulación 1: Circuito básico para la
caracterización de un MOSFET.
II-A1 Simulación 1.1: Circuito de caracterización.
Como el circuito de caracterización ya esta hecho, solo
se ponen los comandos spice de la simulación.
Para la simulación 1.1. el comando de simulación es el
siguiente.
.t r an
0 1 0 1m
Figura 3: Comando de simulación para el circuito 1.
El siguiente es el comando spice para variar la resistencia.
.st ep
par am
r
1k
10k
1
Figura 4: Comando spice para variar la resistencia.
Figura 5: Circuito de simulación 1.2..
Como se ve en la figura anterior, el circuito se parece
al de la simulación 1.1. visto en la guía pero el source y
drain ya no están conectados. Por lo que VGS = VG . Para
obtener el valor máximo del pulso de la fuente del drain
se conoce el valor VDS e Id, y se toma una resistencia de
valor comercial de 1 Ω para que el valor de VDD no difiera
mucho de VDS .
VDD − VDS
= ID
R
VDD = I D (R) + VDS
VGS max
La idea de los circuitos de la simulación 1.2. es obtener
una curva I D vsVDS para ciertos valores de VGS . Por este
motivo se toma en cuenta las curvas vistas en las figuras
2 y 1. Como la idea es obtener todas las curvas en una
única simulación, y esto no es posible si en ltspice si se
tiene mas de una variable. Se usara un único comando .step
para variar la tensión VGS . La única resistencia a usar sera
constante pues solo se puede variar con el comando .step y
se encuentra entre drain y VDD , y la fuente VDD variara pero
usando un pulso que va desde 0 hasta un valor máximo
calculado. En este caso no hay problema en usar un pulso
(2)
Como en las figuras 2 y 1 no se observan los valores en los
cuales las curvas con mayores valores de VGS , se tomo una
regla de 3 de manera que el valor máximo de VDD sigue
que:
VDD max
II-A2 Simulación 1.2: Diseño de circuito para la obtención de
gráfica I D vs VDS
(1)
=
VDD
VGS
VDD max = VGS max
(3)
VDD
VGS
(4)
Si bien el método no es preciso, lo importante es que el
valor de VDD máximo permita que la curva sea mostrada,
lo importante es seleccionar un curva cuyos valores sean
fácilmente visibles. Por esto, para la figura 1 del transistor
BSS138 se eligió la curva para VGS =2V con un valor de I D
= 0.175A y VDS en saturación de VDS =1V. Para la figura 2
del transistor 2N7000 se eligió la curva de VGS = 3V con
I D =0.053 y para VDS en saturación VDS =1V . Así se tiene
que:
VDD B SS138 = 0.175A(1Ω) + 1V = 1.175V
(5)
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
VDD 2N 7000 = 0.05A(1Ω) + 1V = 1.053V
(6)
(11)
Tambien se tienen la siguientes condiciones generales:
Se obtiene VDD máximo.
1.175V
= 5.875V
2V
1.05V
= 10V
= 3.5V
3V
VDD max = 10V
(7)
VDD max
(8)
C 1 = C 2 = C 3 = C s = 10µF
0 500ms
(12)
f = {1, 1k, 10k, 100k, 1M }H z
Con esto ya se tiene suficiente información para hacer los
comandos spice, el comando de simulación es igual para
los dos transistores:
.t r an
3
(13)
II-B1 Análisis DC y punto de polarización DC para amplificadores de fuente común, fuente común degenerada y
compuerta común:
0 1m
Figura 6: Comando de simulación S1.2
II-A2a Los comandos para las fuentes VDD y VG en el
transistor BSS138:
PU LSE (0 11 1p
500ms
500ms
1p
1000ms)
Figura 7: Comando spice para variar la fuente VDD
.st ep
par am
vg
3 10 1
Figura 8: Comando spice para variar la fuente VG
Figura 11: Circuito en DC de amplificador fuente común.
Se obtiene el valor de VG usando divisor de tensión:
II-A2b Los comandos para las fuentes VDD y VG en el
transistor 1N47000:
VG =
RG2
VDD
RG1 + RG2
(14)
Con el valor de VG se obtiene el valor de VGS :
VGS = VG − I D (R S )
PU LSE (0 11 1p
500ms
500ms
1p
1000ms)
Se recuerda que el valor de I D para un NMOS es:
Figura 9: Comando spice para variar la fuente VDD
.st ep
par am
vg
l i st
ID =
2 2.5 3 3.5 4.5 6 10
VG −
A
K nB SS138 = 0.6189 2
V
VT N2N 7000 = 2, 235V
A
K n2N 7000 = 0, 0906 2
V
(9)
(10)
(16)
Kn
(VGS − VT N )2 (R S ) = VGS
2
Kn
(VGS − VT N )2 R S − VG = 0
2
¡ 2
¢
Kn
VGS +
R S VGS
− 2VGS VT N + VT2N − VG = 0
2
VGS +
II-B Simulación 2: de amplificadores con MOSFETs.
Para esta simulación se usaran los valor de VT N y K n
obtenidos en el procedimiento de la simulación 1 y que se
explican en los resultados y análisis, estos son:
Kn
(VGS − VT N )2
2
Sustituyendo la ecuación 16 en la ecuación 15
Figura 10: Comando spice para variar la fuente VG
VT NB SS138 = 1, 294V
(15)
Si
Kn
2
(17)
(18)
(19)
RS = K
2
VGS + kVGS
− 2VT N kVGS + VT2N k − VG = 0
(20)
2
kVGS
(21)
+ VGS − 2VT N kVGS + VT2N k − VG
=0
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
¡
¢
2
kVGS
+ (1 − 2VT N k)VGS + VT2N k − VG = 0
(22)
4
II-B2b Análisis AC:
(23)
De esta manera se tiene una ecuación cuadrática de la
forma:
ax 2 + bx + c = 0
(24)
En la que se tiene que:
x = VGS
(25)
Kn
a =k =
RS
2
(26)
µ
¶
Kn
b = (1 − 2VT N k) = 1 − 2VT N
RS
2
Kn
c = VT2N k − VG = VT2N
R S − VG
2
Así se puede obtener VGS :
(27)
(28)
Figura 12: Circuito en AC de amplificador fuente común.
1 − 2VT N K2n R S
VGS = −
2 (K n R S )
r³
±
³
´2
´³
1 − 2VT N K2n R S − 4 K2n R S VT2N K2n R S
2
³
Kn
2 RS
− VG
´ (29)
La figura 12 enseña el circuito del amplificador en fuente
común para
´
De esta manera se pueden obtener se obtienen dos valores distintos para VGS , siendo estos VGS 1 y VGS 2 . Usando la
ecuación 16 se pueden obtener dos valores para I D siendo
estos I D 1 y I D 2 . Usando ley de voltajes de Kirchhoff para
obtener VDS se tiene:
I D 1,2 R D + VDS 1,2 + I D R S = VDD
(30)
VDS 1,2 = VDD − I D 1,2 R D − I D 1,2 R S
(31)
VDS 1,2 = VDD − I D 1,2 (R D + R S )
(32)
Luego de que se obtienen los dos valores de VDS se
procede a comprobar la condición de saturación para el
transistor:
VDS 1,2 ≥ VGS 1,2 − VT N
Figura 13: Circuito en AC en modelo de pequeña señal amplificador fuente
común.
(33)
Así se elije cualquier uno de los dos valores de VDS que
cumpla la condición vista en la ecuación 33
II-B2 Simulación 2.1: Amplificador CMOS de Fuente Común.
II-B2a Condiciones para calculo de la simulación 2.1
II-B2c Obtención de parámetros:
Impedancia de entrada Zi n :
Como se ve en la figura 13 la impedancia de entrada Zi n
será igual a:
Zi n = R i n + RG1 ||RG2
1
Zi n = R i n + 1
1
R +R
G1
R L = 10kΩ
(34)
Vi n p = 0.05V
(35)
Vout p = 0.25V
Vout p
=5
Av =
Vi n p
f i ni ci al = 10k H z
(36)
(37)
(38)
(39)
(40)
G2
Impedancia de salida Zout :
Como se ve en la figura 13 la impedancia de salida Zout
será igual a:
Zout = R o ||R D ||R L
1
Zout = 1
1
1
Ro + R + R
D
L
(41)
(42)
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
Sin embargo, puede darse el caso en que la resistencia R o
es lo suficientemente grande como para que su efecto en
Zi n sea despreciable, en ese caso Zi n es:
Zout = R D ||R L
1
Zout = 1
1
R +R
D
(43)
(45)
(46)
(47)
Luego se obtiene el valor del voltaje de salida Vout :
Vout = −g m Vg s Zout
(48)
Vout = −K n (VGS − VT N )Vg s Zout
(49)
Así se obtiene el valor de la ganancia:
Av =
Vg s R
Zi n
G1 ||RG2
µ
A v = −K n (VGS − VT N )
¶
RG1 ||RG2
Zout
Zi n
Sustituyendo el valor de VGS por el visto en 46
¶
µ
RG1 ||RG2
A v = −K n (VGS − VT N )
Zout
R i n + RG1 ||RG2
Para obtener RD , se empieza por despejar ZD :
¶
µ
RG1 ||RG2
Zout
A v = −K n (VGS − VT N )
R + RG1 ||RG2
µ in
¶
Av
R i n + RG1 ||RG2
Zout = −
K n (VGS − VT N )
RG1 ||RG2
A v (R i n + RG1 ||RG2 )
Zout = −
K n (VGS − VT N ) (RG1 ||RG2 )
(62)
RG1 = RG2 = 10M Ω
Primero se obtiene el valor de la tensión de entrada Vi n
Vout
Vi n
−K n (VGS − VT N )Vg s Zout
Para el circuito amplificador en fuente común del transistor 2N7000 se tienen los siguientes parámetros:
VDD = 5V
Ganancia de voltaje del amplificador A v :
Av =
II-B2d Parámetros para transistor 2N7000
(44)
L
RG1 ||RG2
Vg s =
Zi n
Zi n
Vi n = V g s
RG1 ||RG2
R i n + RG1 ||RG2
Vi n = V g s
RG1 ||RG2
5
(50)
(51)
(52)
(53)
(64)
R i n = 50Ω
(65)
R L = 10kΩ
(66)
VT N = 2.235V
(67)
K n = 0.0906
A
V2
Av = 5
(55)
(56)
(68)
(69)
El valor de VDD se eligió tomando en cuenta las limitaciones que puede tener la fuente en la práctica. Los valores de
RG1 Y RG2 se eligieron pensando en la obtención del valor
VG , también se tomo el valor mas grande de resistencia
comercial disponible debido a que el transistor presenta
un mejor comportamiento cuando la corriente por VG es
pequeña. Ri n es un valor aproximado a los acoples que se
usan en la fuente .Los valores de R L , K n , VT N y A v son
condiciones que no se pueden cambiar como se menciono
antes.
II-B2e Análisis para transistor 2N7000
Usando la ecuación 14 para la obtención del valor de VG ,
se tiene que:
VG = 0.5VDD = 2.5V
(54)
(63)
R S = 1Ω
(70)
Usando la ecuación 29 para la obtención de los valores
de VGS se tiene:
VGS 1 ' 2, 4968V
(71)
VGS 2 ' −19, 4801V
(72)
Ahora se puede despejar el valor de Zout :
Zout =
1
1
RD
+ R1
L
1
1
1
=
+
Zout R D R L
1
1
1
=
−
RD
Zout R L
µ
¶
1
1 −1
RD =
−
Zout R L
µ
¶
K n (VGS − VT N ) (RG1 ||RG2 )
1 −1
RD = −
−
A v (R i n + RG1 ||RG2 )
RL
(57)
(58)
(59)
(60)
A partir de estos valores se pueden obtener los valores
correspondientes para ID usando la ecuación 16:
I D 1 ' 3, 17088m A
(73)
I D 2 ' 21.98A
(74)
Con estos valores ahora es necesario obtener el valor de
RD para poder continuar con el análisis. Para esto se usa la
ecuación 61, para la cual ya se cuentan con todos los datos
necesarios, así se tienen dos valores de R D :
(61)
R D 1 ' 210Ω
(75)
R D 2 ' −2Ω
(76)
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
Dado que el valor de R D 2 es negativo se descarta para
el valor de VGS 2 , esto era previsible pues el valor de I D 2
superaba por mucho la corriente que puede manejar el
transistor. Ahora se obtiene el valor de VDS usando la
ecuación 32:
6
II-B2f Parámetros para transistor BSS138
Para el circuito amplificador en fuente común del transistor 2N7000 se tienen los siguientes parámetros:
(77)
VDD = 3V
Se comprueba la condición de operación de la ecuación 33:
R S = 1Ω
(91)
R i n = 50Ω
(92)
VDS ' 4, 3510V
4, 3510 ≥ 2, 4968V − 2.236V
(78)
Como se puede observar la condición se cumple.
Para la resistencia R D 1 se selecciona el valor mas cercano
de resistencia comercial, así R D 1 será:
R D 1 = 220Ω
(79)
Ahora con estos nuevos valores se obtienen los nuevos
datos de VGS ,VDS y A v , los cuales se muestran a continuación:
VGS = 2, 4969V
(80)
VDS = 4, 3133V
(81)
4, 3133V ≥ 2, 4969V − 2, 235V
RG1 = RG2 = 10M Ω
R L = 10kΩ
(93)
VT N = 1.35V
A
K n = 1.1 2
V
Av = 5
(94)
(83)
Como el valor de la ganancia es aproximadamente 2.1 %
mayor al pedido como condición. Por lo que la elección
del valor comercial de R D es aceptable.
Ahora se obtiene el valor de la potencia en cada una de
las 5 resistencias en la configuración (se excluye Ri n que
corresponde a la resistencia de los acoples de la fuente).
P RG1 =
VG2
(2.5V )2
= 6.25µW
RG2
RG2
1M Ω
2
= ID
R D = (3.11m A)2 (220Ω) = 2.13mW
P RG2 =
P RD
RG1
VR2G2
(VDD − VG )2 (2.5V )2
=
=
= 6.25µW
RG1
1M Ω
2
P RS = I D
RS
2
V
R RL = out
RL
=
=
2
= (3.11m A) (1Ω) = 9, 67µW
(84)
(85)
(86)
(87)
2
(0.25V )
=
= 6.25µW
10K Ω
(95)
(96)
El valor de VDD se eligió tomando en cuenta las limitaciones que puede tener la fuente en la práctica. Los valores de
RG1 Y RG2 se eligieron pensando en la obtención del valor
VG , también se tomo el valor mas grande de resistencia
comercial disponible debido a que el transistor presenta
un mejor comportamiento cuando la corriente por VG es
pequeña. Ri n es un valor aproximado a los acoples que se
usan en la fuente .Los valores de R L , K n , VT N y A v son
condiciones que no se pueden cambiar como se menciono
antes.
II-B2g Análisis para transistor BSS138
Usando la ecuación 14 para la obtención del valor de VG ,
se tiene que:
VG = 0.5VDD = 2.5V
VR2G1
(90)
(82)
Se cumple la condición para saturación. Ahora se observa
el valor de AV
AV = 5.107
(89)
(88)
Como todos los valores de potencia son tan pequeños,
se puede usar cualquier resistencia comercial.
(97)
Usando la ecuación 29 para la obtención de los valores
de VGS se tiene:
VGS 1 ' 1, 4893V
(98)
VGS 2 ' −0, 6075V
(99)
A partir de estos valores se pueden obtener los valores
correspondientes para ID usando la ecuación 16:
I D 1 ' 10, 676m A
(100)
I D 2 ' 2, 107A
(101)
Con estos valores ahora es necesario obtener el valor de
RD para poder continuar con el análisis. Para esto se usa la
ecuación 61, para la cual ya se cuentan con todos los datos
necesarios, así se tienen dos valores de R D :
R D 1 ' 33Ω
(102)
R D 2 ' −2Ω
(103)
Dado que el valor de R D 2 es negativo se descarta para el
valor de VGS 2 . Ahora se obtiene el valor de VDS usando la
ecuación 32:
VDS ' 2, 6398V
(104)
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
Se comprueba la condición de operación de la ecuación 33:
2, 6398 ≥ 1, 4893V − 1, 35V
7
II-B3b Análisis AC:
(105)
Como se puede observar la condición se cumple.
La resistencia R D 1 ya es un valor comercial de resistencia.
Por esto, ahora se puede obtener el valor de la potencia
en cada una de las 5 resistencias en la configuración (se
excluye Ri n que corresponde a la resistencia de los acoples
de la fuente).
P RG1 =
RG1
VR2G2
=
(VDD − VG )2 (2.5V )2
=
= 6.25µW
RG1
1M Ω
VG2
(2.5V )2
= 6.25µW
RG2
RG2
1M Ω
2
= ID
R D = (10.676m A)2 (33Ω) = 3.76mW
P RG2 =
P RD
VR2G1
=
=
2
P RS = I D
R S = (10.676m A)2 (1Ω) = 114µW
R RL =
2
Vout
RL
(106)
Figura 14: Circuito en AC de amplificador fuente degenerada.
(107)
(108)
(109)
2
=
(0.25V )
= 6.25µW
10K Ω
(110)
Como todos los valores de potencia son tan pequeños,
se puede usar cualquier resistencia comercial.
II-B2h Obtención de valores limite de pequeña señal:
II-B2i Gráficas de recta de carga AC y DC:
Figura 15: Circuito en AC en modelo de pequeña señal amplificador fuente
degenerada.
II-B2j Función de transferencia Vi n vs Vout :
II-B3 Simulación 2.2: Amplificador CMOS de Fuente Degenerada.
II-B3c Obtención de parámetros:
A partir de la imagen 15 se puede observar que al aplicar
ley de voltajes de Kirchhoff se obtiene el valor Vi n :
Vi n = V g s + V s
II-B3a Condiciones para calculo de la simulación 2.2
R L = 2kΩ
(111)
Vi n p = 0.05V
(112)
Vout p = 0.3V
Vout p
Av =
=6
Vi n p
(113)
(115)
Vi n = V g s + I s R S
(116)
Vi n = Vg s + (g m Vg s )R S
(117)
Vi n = Vg s (1 + g m R S )
(118)
Ganancia de voltaje del amplificador A v :
Si R o = ∞, la impedancia de salida Zout es:
(114)
Zout = R D ||R L
(119)
Vout = −g m Vg s Zout
(120)
Entonces Vout es:
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
Asi la ganacia A v es:
Av =
Av =
Vout
Vi n
−g m Vg s Zout
Vg s (1 + g m R S )
−g m Zout
Av =
1 + g m RS
(121)
(122)
8
RG1 Y RG2 se eligieron pensando en la obtención del valor
VG , también se tomo el valor mas grande de resistencia
comercial disponible debido a que el transistor presenta
un mejor comportamiento cuando la corriente por VG es
pequeña. .Los valores de R L , K n , VT N y A v son condiciones
que no se pueden cambiar como se menciono antes.
(123)
II-B3e Análisis para transistor 2N7000
Impedancia de salida Zout :
Con la ecuación 123 para la ganancia se puede obtener
el valor de R D al obtener primero Zout :
VG = 0.5VDD = 2.5V
−g m Zout
= Av
1 + g m RS
Zout
(124)
1 + g m RS
= −A v
gm
Ahora se obtiene R D :
¶
µ
1 −1
1
+
= Zout
RD RL
1
1
1
+
=
R D R L Zout
1
1
1
=
−
RD
Zout R L
µ
¶
1 −1
1
1
=
−
RD
Zout R L
µ
¶
gm
1 −1
1
¡
¢−
= −
RD
RL
A v 1 + g m RS
(125)
(126)
(128)
(129)
(130)
La impedancia de entrada es, como se ve en la figura 15,
las resistencias RG1 y RG2 en paralelo.
Zi n = RG1 ||RG2
1
Zi n = 1
1
R +R
Usando la ecuación 29 para la obtención de los valores
de VGS se tiene:
VGS 1 ' 2, 4863V
(141)
VGS 2 ' −2, 5792V
(142)
A partir de estos valores se pueden obtener los valores
correspondientes para ID usando la ecuación 16:
I D 1 ' 2, 9195m A
(143)
I D 2 ' 1, 0807A
(144)
Con estos valores ahora es necesario obtener el valor de
RD para poder continuar con el análisis. Para esto se usa la
ecuación 61, para la cual ya se cuentan con todos los datos
necesarios, así se tienen dos valores de R D :
R D 1 ' 333Ω
(145)
R D 2 ' 15Ω
(146)
Ahora se obtiene VDS usando la ecuación 32:
(131)
VDS 1 ' 4, 0144V
(147)
(132)
VDS 2 ' −16, 2286V
(148)
G2
Se comprueba la condición de operación de la ecuación 33:
VDS 1 = 4, 3510 ≥ 2, 4968V − 2.236V
II-B3d Parámetros para transistor 2N7000
VDS 2 = −16, 2286V ≤ −2, 5792V − 2.236V
Para el circuito amplificador en fuente común del transistor 2N7000 se tienen los siguientes parámetros:
VDD = 5V
(133)
RG1 = RG2 = 10M Ω
(134)
R S = 4.7Ω
(135)
R L = 2kΩ
(136)
VT N = 2.235V
(137)
K n = 0.0906
Av = 6
A
V2
(140)
(127)
Impedancia de entrada Zi n :
G1
Usando la ecuación 14 para la obtención del valor de VG ,
se tiene que:
(138)
(139)
El valor de VDD se eligió tomando en cuenta las limitaciones que puede tener la fuente en la práctica. Los valores de
(149)
(150)
Se observa que la condición solo se cumple para VDS 1
Para la resistencia R D 1 se selecciona el valor mas cercano
de resistencia comercial, así R D 1 será:
R D 1 = 330Ω
(151)
Ahora con estos nuevos valores se obtienen los nuevos
datos de VGS ,VDS y A v , los cuales se muestran a continuación:
VGS = 2, 4862V
(152)
VDS = 4, 0158V
(153)
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
4, 0158V ≥ 2, 4862V − 2, 235V
(154)
Se cumple la condición para saturación. Ahora se observa
el valor de AV
AV = 5.97
P RG1 =
=
2
(2.5V )
(VDD − VG )
=
= 625nW
RG1
10M Ω
VG2
(2.5V )2
= 625nW
RG2
RG2
10M Ω
2
= ID
R D = (3.11m A)2 (330Ω) = 2.85mW
P RG2 =
P RD
RG1
VR2G2
2
2
P RS = I D
RS
2
V
R RL = out
RL
=
Usando la ecuación 29 para la obtención de los valores
de VGS se tiene:
(155)
El valor de la ganancia es aproximadamente EL 99.5 % de
la ganancia pedida como condición. Por lo que la elección
del valor comercial de R D es aceptable.
Ahora se obtiene el valor de la potencia en cada una de
las 5 resistencias en la configuración (se excluye Ri n que
corresponde a la resistencia de los acoples de la fuente).
VR2G1
9
=
2
= (3.11m A) (4, 7Ω) = 40, 6µW
(156)
(0.3V )
=
= 45µW
2K Ω
VGS 2 ' 0, 8798V
(170)
I D 1 ' 7, 113m A
(171)
I D 2 ' 122m A
(172)
Con estos valores ahora es necesario obtener el valor de
RD para poder continuar con el análisis. Para esto se usa la
ecuación 61, para la cual ya se cuentan con todos los datos
necesarios, así se tienen dos valores de R D :
(158)
(159)
(169)
A partir de estos valores se pueden obtener los valores
correspondientes para ID usando la ecuación 16:
(157)
2
VGS 1 ' 1, 4637V
R D 1 ' 82Ω
(173)
R D 2 ' 19Ω
(174)
Ahora se obtiene VDS usando la ecuación 32:
(160)
Como todos los valores de potencia son tan pequeños,
se puede usar cualquier resistencia comercial.
VDS 1 ' 2, 3820V
(175)
VDS 2 ' 0, 0469V
(176)
Se comprueba la condición de operación de la ecuación 33:
II-B3f Parámetros para transistor BSS138
Para el circuito amplificador en fuente común del transistor BSS138 se tienen los siguientes parámetros:
VDD = 3V
(161)
RG1 = RG2 = 10M Ω
(162)
R S = 5, 1Ω
(163)
R L = 2kΩ
(164)
VT N = 1.35V
A
K n = 1, 1 2
V
Av = 6
(165)
(166)
(167)
El valor de VDD se eligió tomando en cuenta las limitaciones que puede tener la fuente en la práctica. Los valores de
RG1 Y RG2 se eligieron pensando en la obtención del valor
VG , también se tomo el valor mas grande de resistencia
comercial disponible debido a que el transistor presenta
un mejor comportamiento cuando la corriente por VG es
pequeña. .Los valores de R L , K n , VT N y A v son condiciones
que no se pueden cambiar como se menciono antes.
II-B3g Análisis para transistor BSS138
Usando la ecuación 14 para la obtención del valor de VG ,
se tiene que:
VG = 0.5VDD = 2.5V
(168)
VDS 1 = 2, 3820V ≥ 1, 4637V − 1, 35V
(177)
VDS 2 = 0, 0469V ≤ 0, 8798V − 1.35V
(178)
Se observa que la condición solo se cumple para VDS 1
Para la resistencia R D 1 se selecciona el valor mas cercano
de resistencia comercial, así R D 1 será:
R D 1 = 330Ω
(179)
Ahora con estos nuevos valores se obtienen los nuevos
datos de VGS ,VDS y A v , los cuales se muestran a continuación:
VGS = 2, 4862V
(180)
VDS = 4, 0158V
(181)
4, 0158V ≥ 2, 4862V − 2, 235V
(182)
Se cumple la condición para saturación. Ahora se observa
el valor de AV
AV = 5.97
(183)
El valor de la ganancia es aproximadamente EL 99.5 % de
la ganancia pedida como condición. Por lo que la elección
del valor comercial de R D es aceptable.
Ahora se obtiene el valor de la potencia en cada una de
las 5 resistencias en la configuración (se excluye Ri n que
corresponde a la resistencia de los acoples de la fuente).
P RG1 =
VR2G1
RG1
=
(VDD − VG )2 (2.5V )2
=
= 625nW
RG1
10M Ω
(184)
Taller del laboratorio No.4.
VG2
(2.5V )2
= 625nW
RG2
RG2
10M Ω
2
= ID
R D = (3.11m A)2 (330Ω) = 2.85mW
P RG2 =
P RD
VR2G2
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
2
P RS = I D
RS
2
V
R RL = out
RL
=
=
2
(185)
10
Para la obtención de los valores VGS 1,2 suponiendo que
se cuenta con el valor de I D se tiene que:
(186)
= (3.11m A) (4, 7Ω) = 40, 6µW
(187)
(0.3V )2
=
= 45µW
2K Ω
(188)
Como todos los valores de potencia son tan pequeños,
se puede usar cualquier resistencia comercial.
II-B3h Obtención de valores limite de pequeña señal:
kn
(VGS − VT N )2 = I D
2
2I D
(VGS − VT N )2 =
K
sn
2I D
VGS − VT N =
Kn
s
2I D
VGS =
+ VT N
Kn
(193)
(194)
(195)
(196)
II-B3i Gráficas de recta de carga AC y DC:
Para obtener el valor de VDS se usa la ley de voltajes de
Kirchhoff en I D , así se tiene:
II-B3j Función de transferencia Vi n vs Vout :
II-B4 Simulación 2.3: Amplificador CMOS de Drenador Común.
II-B4a Condiciones para calculo de la simulación 2.3
VDD = VDS + I D R S
(197)
VDS = VDD − I D R S
(198)
De esta manera se puede cumplir comprobar la condición de saturación vista en la ecuación 33.
Conociendo el valor de VGS se puede obtener VG de la
siguiente manera:
R L = 100Ω
(189)
Vi n p = 0.1V
(190)
f i ni ci al = 10k H z.
(191)
VG + V S = VGS
VG = VGS + I D R S
(199)
(200)
II-B4b Análisis DC y punto de polarización DC:
II-B4c Análisis AC:
Cuando se observa el modelo en AC, todas las fuentes
DC se apagan y los condensadores se observan en corto.
Así se ve la imagen 17:
Figura 16: Circuito en DC amplificador de drenador común.
Figura 17: Circuito en AC amplificador de drenador común.
Para la obtención del valor de VG se sigue el mismo
procedimiento que en el usado en la sección II-B2, así se
tiene que:
RG1
VG = VDD
(192)
RG2 + RG1
Usando el modelo π en la figura 17 se tiene la figura 18
en la cual no se observa una resistencia r o pues esta se
supone infinita.
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
11
Zout =
1
1
RL
+ R1
(205)
L
Así también se puede obtener a R S si se tiene la impedancia de salida:
1
1
1
+
=
R S R L Zi n
1
1
1
−
=
R S Zi n R L
¶
µ
1 −1
1
−
RS =
Zi n R L
(206)
(207)
(208)
Ganancia de voltaje del amplificador A v :
Como se ve en la figura 19 el voltaje de salida Vout será:
Figura 18: Circuito en AC en modelo de pequeña señal amplificador de drenador
común.
Como se observa en la figura 17, drain se encuentra
conectado a tierra y el voltaje de salida Vout se encuentra
conectado a source. De esta manera las resistencias R S , R L
y la fuente g m Vg s se encuentran en paralelo como se ve en
la figura 19
Vout = Vg s g m Zout
(209)
También si se realiza ley de voltajes de Kirchhoff se
observa que Vi n es:
Vi n = Vg s + Vg s g m Zout
(210)
Asi, se puede obtener la ganancia A v como:
Av =
Av =
Av =
Av =
Vout
Vi n
Vg s g m Zout
Vg s + Vg s g m Zout
Vg s g m Zout
−1
Vg s g m (g m
+ Zout )
Zout
−1
gm
+ Zout
(211)
(212)
(213)
(214)
Si ya se cuenta con el valor de la ganancia A v y Zout
,entonces se puede obtener g m de la siguiente manera:
Zout
Figura 19: Circuito en AC en modelo simplificado de pequeña señal amplificador
de drenador común.
−1
gm
+ Zout
= Av
¡ −1
¢
Zout = A v g m
+ Zout
(216)
−1
Zout = A v g m
+ A v Zout
(217)
Zout − A v Zout =
Zout (1 − A v ) =
II-B4d Obtención de parámetros:
Impedancia de entrada Zi n :
Como se observa en la figura 19 la impedancia de entrada
será la suma de las resistencias en paralelo de RG1 Y RG2
Zi n = RG1 ||RG2
1
Zi n = 1
1
+
R
R
G1
Zi n =
(215)
−1
Av gm
−1
Av gm
Av
Zout =
g m (1 − A v )
Av
gm =
Zout (1 − A v )
(218)
(219)
(220)
(221)
(201)
(202)
II-B4e Parámetros para transistor 2N7000
G2
RG1 RG2
RG1 + RG2
(203)
Para el circuito amplificador en fuente común del transistor 2N7000 se tienen los siguientes parámetros:
Impedancia de salida Zout :
VDD = 12V
Como se observa en la figura 19 la impedancia de salida
será la suma de las resistencias en paralelo de R S Y R L
Zout = R L ||R S
(204)
(222)
R S = 3900Ω
(223)
R L = 100Ω
(224)
VT N = 2.236V
(225)
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
K n = 0.0932
A
V2
(226)
Vi n = 0.1V
(227)
A v = 0.6
(228)
Los parámetros de A v y R S se eligieron arbitrariamente.
12
De esta manera se puede obtener el valor de VG usando
la ecuación 200:
VG = 2.4V + 1, 27m A(3900Ω)
(246)
VG ' 7.353V
(247)
Ahora se busca obtener el valor de RG1 y RG2 , primero
se ve que según la ecuación 203 :
II-B4f Análisis para transistor 2N7000
Con el valor de R S y R L se puede obtener Zout :
µ
¶
1
1 −1
Zout =
+
RS RL
¶
µ
1
1 −1
Zout =
+
Ω
3900 100
Zout = 97.5Ω
(229)
(230)
(231)
Usando la ecuación 221 se obtiene el valor de g m .
Av
Zout (1 − A v )
0.6
gm =
97.5Ω(1 − 0.6)
A
g m ' 0, 0154
V
Se puede obtener ID recordando que g m es también:
p
2K n I D = g m
(232)
gm =
2
2K n I D = g m
ID =
2
0, 01542 VA 2
´
ID = ³
2 0, 0932 vA2
(235)
I D ' 1, 27m A
(236)
Usando la ecuación 196 para obtener VGS y sustituyendo
ID .
v ³
u g2 ´
u2 m
t 2K n
+ VT N
(237)
VGS =
Kn
gm
VGS =
+ VT N
(238)
Kn
0, 0154 VA
VGS =
+ 2.235V
(239)
0.0932 VA2
VGS ' 2.4V
VDS = VDD − I D R S
(241)
VDS = 12V − (1, 27m A)(3900Ω)
(242)
VDS = 7.047V
(243)
Así se comprueba la condición de saturación.
(244)
7.047V ≥ 2.4V − 2.235V
(245)
(254)
Por lo tanto, el valor de Zi n es:
7.353V
12V
Zi n = 613kΩ
Zi n = 1M Ω
RG2 se puede obtener entonces como:
µ
¶
1 −1
1
−
RG2 =
Zi n RG1
¶−1
µ
1
1
RG2 =
−
613kΩ 1M Ω
RG2 ' 1.58M Ω
(255)
(256)
(257)
(258)
(259)
Se escoge la resistencia de valor comercial mas cercano
para RG2 , asi se tiene que:
RG2 = 1, 5M Ω
(260)
Así se comprueba el cambio en el valor de VG .
1, 5M Ω
1, 5M Ω + 1M Ω
VG = 7, 2V
VG = 12V
(261)
(262)
El cambio es de un 2 % del valor original calculado para
VG , por lo que los valores elegidos para las resistencias RG1
y RG2 son aceptables.
Ahora se obtiene el valor de potencia para cada una de
las 4 resistencias:
VR2G1
(VDD − VG )2
RG1
RG1
(12V − 7.353V )2 (4.647V )2
=
= 21.6µW
=
1M Ω
1M Ω
P RG1 =
VDS ≥ VGS − VT N
(249)
RG1 = 1M Ω
(240)
Ahora se obtiene VDS usando la ecuación 198 y sustituyendo a I D .
Zi n
RG1
Por medio de iteración entre los valores comerciales de
resistencias se eligió:
(234)
2K n
(248)
Se puede ver que este valor se puede sustituir en la
ecuación 192
RG2
VDD
= VG
(250)
RG1 + RG2
Zi n
VDD
= VG
(251)
RG1
VG
(252)
Zi n = RG1
VDD
(253)
(233)
2
gm
RG1 RG2
RG1 + RG2
RG2
=
RG1 + RG2
Zi n =
=
(263)
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
13
II-B6a Condiciones para calculo de la simulación 2.5
VG2
2
(7.353V )
= 36µW
RG1
RG1
1.5M Ω
2
= ID
R S = (1.27m A)2 (3900Ω) = 6, 29mW
P RG2 =
P RS
VR2G2
P RL =
=
2
VOU
T
RL
=
(264)
(265)
2
(0.06V )
=
= 36µW
100Ω
(266)
R L = 220Ω
(272)
Vi n p = 0.05V
(273)
Vout p =?
Vout p
=?
Av =
Vi n p
II-B4g Gráficas de recta de carga AC y DC:
f i ni ci al = 10k H z.
(274)
(275)
(276)
II-B4h Función de transferencia Vi n vs Vout :
II-B6b Análisis DC y punto de polarización DC:
II-B5 Simulación 2.4: Amplificador CMOS de Compuerta Común.
II-B6c Análisis AC:
II-B5a Condiciones para calculo de la simulación 2.4
II-B6d Obtención de parámetros:
Ganancia de voltaje del amplificador A v :
Impedancia de entrada Zi n :
R L = 10kΩ
(267)
Vi n p = 0.05V
(268)
Vout p = 0.1V
Vout p
Av =
=2
Vi n p
f i ni ci al = 10k H z.
Impedancia de salida Zout :
(269)
(270)
(271)
II-B5b Análisis DC y punto de polarización DC:
II-B6e Obtención de valores limite de pequeña señal:
II-B6f Gráficas de recta de carga AC y DC:
II-B6g Función de transferencia Vi n vs Vout :
III Resultados y análisis.
III-A S.1. Resultados y análisis:
II-B5c Análisis AC:
II-B5d Obtención de parámetros:
Ganancia de voltaje del amplificador A v :
III-A1 S1.1. resultados y análisis:
Impedancia de entrada Zi n :
Impedancia de salida Zout :
II-B5e Obtención de valores limite de pequeña señal:
II-B5f Gráficas de recta de carga AC y DC:
II-B5g Función de transferencia Vi n vs Vout :
II-B6 Simulación 2.5: Amplificadores en Cascada.
Figura 20: Circuito de la simulación 1 con el transistor BSS138.
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
La figura 20 muestra la gráfica de la raíz cuadrada de
la corriente vs tensión VGS para el transistor BSS138. La
ecuación de obtenida para la recta es:
p
I = 0, 5563x − 0, 7199
(277)
De esta manera la intersección en el eje x es:
(279)
VT N = 1, 294V
(281)
(278)
(280)
Se observa que el valor obtenido es muy cercano al valor
típico visto la tabla I pues la diferencia es apenas de 0,006V
. Ahora se obtiene el valor K n .
(289)
(290)
Se observa que el valor obtenido es muy cercano al valor
típico visto la tabla II pues la diferencia es apenas de
0,135V.Ahora se obtiene K n .
(291)
Se toman los valores para una resistencia de 1000 Ω de I D ,
VGS de la simulación, al igual que se usa el valor obtenido
de VT N .
0, 5K n (2, 47V − 2, 235V )2 = 0, 00253A
0, 00253A
Kn =
0, 5(2, 47V − 2, 235V )2
mA
K n = 91, 62 2
V
(292)
(293)
(294)
(282)
Se toman los valores para una resistencia de 1000 Ω de I D ,
VGS de la simulación, al igual que se usa el valor obtenido
de VT N .
0.5K n (1.4V − 1, 294V )2 = 0.0036A
0.0036A
Kn =
0.5(1.4V − 1, 294V )2
mA
K n = 640, 7 2
V
x = 2, 235
VT N = 2, 235V
I D = 0.5K n (VGS − VT N )2
0, 5563x − 0, 7199 = 0
0, 7199
x=
0, 5563
x = 1, 294
I D = 0.5K n (VGS − VT N )2
14
(283)
III-A1a Región de polarización del transistor y su comportamiento:
Drain y Gate se encuentran conectados , por lo tanto, sus
tensiones son igual y la tensión en source es 0 por lo que:
VGS = VDS
(295)
(284)
De esta manera , se cumple la condición para la saturación:
(285)
VDS ≥ VGS − VT N = VDS − VT N
(296)
En adición, el cambio de resistencia no afecta significativamente la región de polarización dado que las condiciones anteriormente explicadas no son dependientes de la
corriente. Sin embargo, el cambio de la corriente afecta el
valor VT N . A medida que la resistencia es menor la corriente
que pasa por ella es mayor aumentando proporcionalmente
el valor de VT N como se ve en la figuras 21 y 20.
III-A1b Comportamiento lineal de la curva
obtención del parámetro VT N :
p
I D vs VGS , y
La razón por la que se encuentra un comportamiento
lineal en las curvas de las figuras 21 y 20, se debe a la
ecuación para encontrar I D .Se observa a continuación.
I D = 0.5K n (VGS − VT N )2
(297)
p
I D = (VGS − VT N ) 0.5K n
(298)
p
p
p
I D = VGS 0.5K n − VT N 0.5K n
(299)
p
Figura 21: Circuito de la simulación 1 con el transistor 2N7000.
La figura 21 muestra la gráfica de la raíz cuadrada de
la corriente vs tensión VGS para el transistor 2N7000. La
ecuación de obtenida para la recta es:
p
I = 0, 2129x − 0, 4758
(286)
De esta manera la intersección en el eje x es:
0, 2129x − 0, 4758 = 0
0, 4758
x=
0, 2129
(287)
(288)
Los valores K n y VT N son constantes, VGS es una variable,
por lo tanto, si se hace 0 a I D se tiene:
p
p
VGS 0.5K n − VT N 0.5K n = 0
(300)
p
VT N 0.5K n
VGS = p
(301)
0.5K n
VGS = VT N
(302)
De esta manera, tambien se explica porque las ecuaciones
de las rectas tienen la forma ax -b y no únicamente ax. El
Taller del laboratorio No.4.
CARACTERIZACIÓN Y AMPLIFICACIÓN CON TRANSISTORES MOSFET
valor de a no es mas que la raíz cuadrada de la constante
K n multiplicado por 0.5. Asi se tiene que:
p
y = ID
(303)
x = VGS
p
a = 0.5K n
p
b = VGS 0.5K n
15
La figura anterior contiene las curvas para VGS a 2V,2.5V
3V,3.5V,4.5V,6V Y 10V siendo la curva de 2V las de color
verde mas cercana al eje x y la de 10V la de color gris mas
alejada.
(304)
(305)
(306)
De esta manera, también se puede estimar un valor para
K n a partir de la la ecuación de la recta obtenida en las
figuras 21 y 20.Siendo K n
p
0.5K n = a
0.5K n = a
(307)
2
K n = 2a
(308)
2
(309)
Así podemos obtener el valor de K n a partir de la constante
a
K nB SS138 = 2(0.5563)2
K n2N 7000 = 2(0.2129)2
(310)
K nB SS138 = 0, 6189
K n2N 7000 = 0, 0906
(311)
Comparado con los valores anteriormente obtenidos vemos
A
A
para BSS138 y 1.02 m
.
que hay una diferencia de 21,8 m
V2
V2
Figura 23: Circuito de la simulación 1.2 con el transistor 2N7000.
(312)
III-A2 S2.1. resultados y análisis:
III-A2a Importancia de las curvas en la gráfica I D vs VGS
y su relación única con el MOSFET:
Las figuras 23 y 22 están hechas para parecerse a las
gráficas correspondientes 2 y 1 de los datasheet.
La figura anterior contiene las curvas dese 1V hasta 10V
siendo la la de 1V la de color azul mas cercana al eje x y
la de 10V la color café mas alejada.
La importancia de estas radica en que se puede observar
dos regiones de operación del transistor en las curvas (no
en todas),especialmente visible en las 4 primeras curvas de
la figura 22 en la que la región plana de la curva es la región
de saturación donde VDS es mayor a Vov , y la parte inicial
de curva corresponde a la región triodo.
Referencias
[1] Taller de laboratorio No. 4: CARACTERIZACIÓN Y AMPLIFICACIÓN
CON TRANSISTORES MOSFET.
[2] Tabla sobre valores de resistencias comerciales - Disponible en:
https://www.electrontools.com/Home/WP/
valores-comerciales-de-resistencias/
[3] D.diode ltspice wiki - Disponible en :
http://ltwiki.org/LTspiceHelp/LTspiceHelp/D_Diode.htm
[4] Microelectronic Sedra Smith. Sexta edición.
[5] Electrónica: Teoría de circuitos y dispositivos electrónicos. Décima
Edición. Robert L. Boylestad. Louis Nashelsky
Figura 22: Circuito de la simulación 1.2 con el transistor BSS138.