República Bolivariana de Venezuela
Ministerio del Poder Popular para la Educación Universitaria
Instituto Universitario Politécnico “Santiago Mariño”
Extensión - Maturín
Relaciones
Profesora:
Alumno:
Diana García
Pedro Montañez
C.I: 29.879.125
Escuela: 47
Maturín, Mayo del 2021
Índice
Introducción……………………………………………………………..…..pág.3
Desarrollo…………………………………………………..……………..pág.4-9
Conclusión………………………………………………………………...pág.10
Mapa Conceptual…………………………………………….…………...pág.11
Ejercicios………………………………………………………….…...pág.12-13
Introducción
Las relaciones se vienen viendo en todas partes pero se aprecia mejor
en las matemáticas en el cual podemos definirlos teóricamente para
ayudar en el procesamiento de información, lo cual saber este
conocimiento es importante, por ese iniciaremos el estudio de que son las
relaciones, las propiedades que presentan como representarlos, entre
otros. Debido el conocimiento que nos puede presentar a futuro como
ingenieros que seremos.
Definición de Relaciones
Las relaciones son una pertenencia de dos elementos entre conjuntos,
en el cual en un conjunto hipotético de A y B cada elemento de A va a ir
enlazado con un elemento de B. Este se representa en pares (a, b)
llamándose grafos el cual define un elemento del primer conjunto (a) y lo
relaciona con el elemento de otro conjunto (b) esto se denomina producto
cartesiano. Las relaciones nos ofrece la posibilidad de manejar grandes
volúmenes de datos de manera simple como también su comprensión
facilitando la toma de decisiones en la vida diaria como por ejemplo en
una organización.
Propiedades de las Relaciones
Reflexiva
Una relación es reflexiva si todos sus elementos que la comprenden
están relacionados consigo mismo, es decir, que todas las parejas
formadas en el R sean parejas que con
componentes que sean
relacionados consigo mismo.
Anti-Reflexiva
A diferencia de la anterior una relación anti-reflexiva es lo contrario en
el cual se cumple si sus elementos no están relacionados consigo mismo
es decir que todas las parejas conformadas en R de los elementos del
conjunto no son iguales.
No Reflexiva
Para que una relación sea no reflexiva todos los elementos que
componen el conjunto originario en donde se van a formar parejas en R
no todas van a estar relacionadas consigo mismas.
Simétrica
Para que una relación sea simétrica en con un conjunto todos los
pares definidos en R tienen que tener su reciproco, es decir, si hay un par
denominado (a, b) también tiene que ver un (b, a) para los pares
reflexivos no hace falta colocar su reciproco ya que es el mismo.
Anti-simétrica
Cuando una relación es anti-simétrica en un conjunto denominado A
los pares originados en R no tienen su reciproco esto afecta a todos así
que si hay un par (a, b) no debe haber un par (b, a).
Relación no simétrica
Este mezcla las características de la anti-simétrica y la simétrica en
conjunto se denomina no simétrica cuando los pares definidos en R
algunos tienen su reciproco pero no todos.
Transitiva
Para que una relación R sea transitiva los elementos deben de estar
relacionado con un segundo y este segundo con un tercero para que el
primero se relacione con el tercero generando un secuencia, es deicr, en
un conjunto A se tiene los elemento m, n y k en donde se cumple esta
propiedad si (m, n) E R y (n, k) E R para que entonces (m, k) E R.
Clasificación de las Relaciones
Relación de orden
Una relación R de un conjunto A es una relación de orden cuando
dicha relación presenta las propiedades de reflexividad, anti-simétrica y
transitiva, es decir, sus elementos se relacionan con el mismo en el
conjunto A, los elementos de R no tienen su reciproco y los elementos de
R se relacionan con un segundo y un tercero.
Relación de equivalencia
Una relación es de equivalencia cuando posee las propiedades
reflexiva, simétrica y transitiva en propiedades es casi igual a la de orden
per cambiando de anti-simétrica a simétrica en el cual esta relación posee
todas la combinaciones posibles de los elementos del conjunto A en R.
Relación binaria
Las relaciones binarias en R comprende que existe entre dos
elementos de a y b de dos conjuntos indicando que el elemento de a está
relacionado con el elemento b. Esta relación puede tener varias
propiedades de las hablas anteriormente, esta se puede representar en
forma de pares ordenados, indicando que aRb o los dos a la vez R(a, b).
Relación de Orden Parcial (Ejemplos)
La relación de orden parcial de R que está definida por un conjunto
denominado A se denomina con ese nombre si contiene las propiedades
reflexiva, asimétrica y transitiva explicadas anteriormente pero en estos
pares no existen una relación entre los elementos de A. Ejemplo:
Sea A = {a, b, c, d, e} y sea una relación sobre A definida por
R = {(a, a), (a, b), (a, c), (a, d), (a, e), (b, b), (b, c), (b, e), (c, c), (c, e), (d,
d), (d, e), (e, e)}
Este es de orden parcial que faltarían pares para completar la
relaciones entre los elementos pero al no se así quedan ciertos ejemplos
sin relacionar siendo como lo dice su nombre relacionado parcialmente,
es decir, por parte.
Relación de Equivalencia (Ejemplos)
Una relación se define de equivalencia en un conjunto denominado A
si estrictamente posee las propiedades reflexivas, simétricas y transitivas
en el cual contiene todas las combinaciones pasibles de cada elemento
del conjunto A. Ejemplo:
Si
A={2,4,5,6,7}
y
R:A→A
es
una
relación
definida
por
R={(2,2),(4,4),(5,5),(6,6),(7,7),(2,4),(4,2),(2,5),(5,2),(2,6),(6,2),(2,7),(7,2),(4
,5),(5,4), (5,6),(6,5),(6,7),(7,6),(4,6),(4,7),(6,4),( 7,4),(5,7),(7,5)}
Esta relación es de equivalencia ya que posee todas la combinaciones se
puede ver pares de (2-7,2-7) de todas formas posibles.
Grafo Dirigido (Ejemplos)
Un grado también denominado dígrafo es una representa de
relaciones en el cual contiene un conjunto de vértices y aristas en donde
cada arista se va a ir asociando a de manera unidireccional con una
flecha con otra arista, las flechas definen si la información es entrante o
saliente en donde siempre tienen un destino de un nodo hacia otro.
Ejemplo:
Si A = {a, b, c, e}
B = {(a, b), (a, c), (a, e), (b, e), (c, e) }
Trayectoria de Grafos Dirigidos
En un grafo dirigido o dígrafo las aristas están representadas por
flechas al ser de esta forma este tienen una trayectoria en el cual se
define viendo los pares ordenados en el cual, el vértice llamado a que
comprendo el elemento a del par ordenado es en donde inicia la flecha y
su destino es el vértice b que es del par ordenado b (a, b), definiendo así
la trayectoria de las aristas y del dígrafo en general.
Conclusión
Para finalizar se ha visto que las relaciones pueden presentar
propiedades que a partir de estas se definen los tipos de relaciones en el
cual nos permiten manejar un volumen de información simplificando las
cosas. Al tener estas propiedades se puede definir qué tipo son, justificar
si un par ordenado pertenece a esa relación y llevado de la mano con sus
representaciones se puede ver cuántas relaciones tiene cada uno y
verificar de manera más grafica cuáles son sus propiedades.
Pedro Montañez
C.I: 29.879.125
Escuela: 47
Relaciones
Las relaciones comprende las pertenencia que tiene un conjuntos
o varios entre si esta mayormente se representa en pares de a y
b llamados pares ordenados (a , b), permitiendo generar un
modelo de base de datos relaciones que nos ayudara a tener
registros y manejar facilmente grandes cantidades de información
Esta comprende
Conceptos Basicos
Producto Cartesiano
Propiedades
Relaciones como
Reflexiva
Tipos de relaciones
Simétrica
Relaciones de orden
Otras
Representaciones
Relaciones de equivalencia
Matricial
El producto cartesiano es una operación de dos
conjuntos que resulta en otro conjunto cuyos
elementos van a estar representado en pares
ordenados el primer elemento del par va a ser
del conjunto 1 y el segundo del conjunto 2, para
indicar que es un producto cartesiano se
representa con un x entre los nombres de los
conjuntos. Ejemplo: AxB
Relación binaria define un subconjunto de dos
conjuntos llamados A y B originado del
producto cartesiano en donde para que sea
una relación binaria los pares ordenados (x, y)
tiene que pertenecer a R relacionándose con y
llegando al caso de que si X = Y se afirma que
los pares ordenados del conjunto R son de
relación binaria
También tiene cosas como:
Relación inversa
La relación reflexiva comprende si los pares
ordenados de una relación R tengas los
componentes o elementos que estén
relacionados con sigo mismo es decir que (a,
b) en donde b = a, también están las antireflexivas en donde ningunas de los
componentes de los pares ordenados están
relacionado consigo mismo y las no reflexivas
en donde solo algunos cumplen esta relación
Para que una relación sea simétrica cada par
ordenado que se presente en dicha relación debe
de tener su reciproco o inverso como lo explicado
anteriormente, es decir, si en R hay un par (a, b)
debe de haber otro (b, a) para que se cumpla esta
propiedad. También esta los anti-simétricos que
ningunos cumplen esta función y los no
simétricos que solamente algunos de los pares
tienen un reciproco
Para que una relación sea de orden la relación
que se presenta debe de tener las propiedades
reflexiva, anti-simétrica y transitiva siendo ya
con estas propiedades de carácter de orden
Una relación es de equivalencia cuando R de
conjunto A contiene las propiedades reflexiva,
simétrica y transitiva, al representarlo en forma
de matriz se puede ver que está lleno de unos (
1)
Esta se divide en
Se pude representar una relación de forma
matricial también llamado Mr en el cual cada
fila y columna contiene los elementos del
conjunto A, en el cual se va a escribir con un
uno (1) la coordenada en donde tenga a "a"
como columna y "b" proveniente del par
ordenado (a, b)como fila los espacios que no
se indicaron se les coloca un cero (0)
Grafos
Los grafos están constituido por vertices que
son círculos que representa a cada elemento del
conjunto unidas por unas aristas que son la
unión o relación en R entre estos, es una forma
mucho más gráfica de representar las
relaciones. Con este también se origina
Digrafos
Transitiva
Dominio
Son todos lo elementos que representa el
primer conjunto representado como Dr = {x E X
tal que (x, y) E R para algún y E Y}
Contradominio
Son todos lo elementos que representa el
segundo conjunto representado como Ir = {y E
Y tal que (x, y) E R para algún x E X}
Las relaciones inversas entre dos conjuntos A y
B en R son los inversos delos pares ordenados
en la relación original, es decir, si el par es (a, b)
la inversa es (b, a)
Relación complementaria
Aplicando esta en un relación R que es igual a {(
1, a),(2, b),(3, c),(4, d)} su conjunto dominio es
Dr= {1, 2, 3, 4} y el conjunto contradominio es
Ir = {a, b, c, d}
La relación complementaria se define como la
sustracción del producto cartesiano con el
conjunto de relación R para darnos este tipo de
relación. Este es representado como A → B tal
que R(complementaria) = {(x, y)/(x, y) } ∉ R}
Una relación se dice que es transitiva cuando
los elementos de los pares están relacionados
con un segundo y ese segundo con un tercero
habiendo un orden en estos o una secuencia en
donde si se tiene este orden el primero se
relaciona con el ultimo
Si A={2,4,5,6,7} y R:A→A es una relación
definida por
R={(2,2),(4,4),(5,4),(5,6),(6,5),(4,5),(4,6),(5,5),(7,
7),(6,6)}
Si A={2,4,5,6,7} y R:A→A es una relación
definida por
R={(2,2),(6,4),(5,6),(6,5),(4,6)}
Si A={2,4,5,6,7} y R:A → A es una relación
definida por R={(2,2),(4,4),(5,5),(6,6),(7,7)}
Relación de orden parcial se cumple las
propiedades de orden pero no todos los pares
o elementos de la relación tienen relación con
el conjunto originario
Relación de orden total en donde se cumplen
las mismas propiedades que las de orden pero
todos los pares ordenados tienen relación con
el conjunto originario
Los dígrafos comprenden lo mismo que un
grafo pero las aristas tienen un dirección que
se pueden ver en forma de flecha. El sentido de
las aristas vienen dado por el elemento "a" de
inicio y elemento "b" final tomando referencia
del par ordenado debido esto los dígrafos
tienen grados internos y externos dependiendo
de la orientación de las aristas
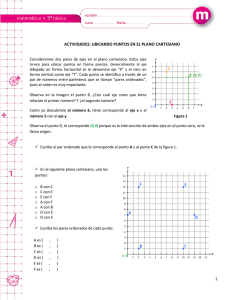
Grafica
Debido a que se puede representar las
relaciones de forma de par ordenado (a, b)
también se puede tomar cada relación que hay
en el conjunto de R y tomarlo como
coordenadas en un eje cartesiano en el cual en
el eje de las X van a ir "a" y el de las Y "b" para
definir los puntos de R