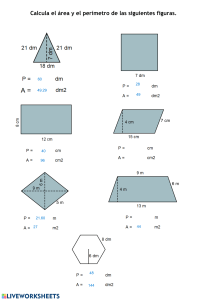
lOMoARcPSD|35117404 GA2-240201528-AA4-EV01 Analisis Y Desarrollo De Software (SENA SofiaPlus) Escanea para abrir en Studocu Studocu no está patrocinado ni avalado por ningún colegio o universidad. Descargado por Marsel Lobo (marselobo123@gmail.com) lOMoARcPSD|35117404 ALGORITMO PARA EL CÁLCULO DE ÁREAS Y VOLÚMENES GA2-240201528-AA4-EV01 Complejo Agroindustrial, Pecuario y Turístico SENA Regional Antioquia Tecnología Análisis y Diseño de Software Descargado por Marsel Lobo (marselobo123@gmail.com) lOMoARcPSD|35117404 Si tuviera un sólido irregular ¿qué método utilizaría para calcular el volumen? Para calcular el volumen de un sólido irregular, se puede utilizar el método de desplazamiento de agua. Este método consiste en sumergir el sólido en un recipiente con agua y medir la diferencia entre el nivel inicial y el nivel final del agua. El volumen del sólido es igual al volumen de agua desplazado. Este método se basa en el principio de Arquímedes, que dice que todo cuerpo sumergido en un fluido experimenta un empuje hacia arriba igual al peso del fluido desalojado. La diferencia entre el volumen final y el inicial es el volumen de la piedra. En este caso, los datos son: Vi = (11,0 ± 0,5) mL Vf = (13,5 ± 0,5) mL Para calcular el volumen de la piedra, se resta el volumen inicial del final: Vp = Vf - Vi Vp = (13,5 ± 0,5) mL - (11,0 ± 0,5) mL Vp = (2,5 ± 1,0) mL El resultado se expresa con una cifra significativa, ya que el dato con menor precisión tiene una cifra decimal. Además, se tiene en cuenta la propagación de incertidumbre al restar cantidades con error absoluto. Por lo tanto, el volumen de la piedra es: Vp = (2,5 ± 1,0) Ml Descargado por Marsel Lobo (marselobo123@gmail.com) lOMoARcPSD|35117404 Figuras Planas CUADRADO AREA A=L*L A=L^2 P=4L El área de un cuadrado se calcula multiplicando la longitud de uno de sus lados por sí misma. Es decir, si L es la longitud de un lado, el área es L x L. El perímetro de un cuadrado se calcula sumando la longitud de los cuatro lados. Como todos los lados son iguales, el perímetro es 4 x L. Por ejemplo, si un cuadrado tiene un lado de 5 cm, su área es 5 x 5 = 25 cm2 y su perímetro es 4 x 5 = 20 cm. TRIANGULO B es la base, H es la altura y A, B y C son los lados del triángulo. Si tenemos un triángulo con una base de 10 cm y una altura de 8 cm, su área sería: Área = (10 x 8) / 2 Área = 40 cm^2 Además, sabemos que los otros dos lados del triángulo miden 12 cm y 13 cm respectivamente, su perímetro sería: Perímetro = 10 + 12 + 13 Perímetro = 35 cm Descargado por Marsel Lobo (marselobo123@gmail.com) lOMoARcPSD|35117404 RECTANGULO AREA A=b*h PERIMETRO P=2B+2H B es la base y H es la altura del rectángulo. Por ejemplo, si tenemos un rectángulo con B = 20 y H = 15, entonces: - Área = 20 x 15 = 300 - Perímetro = 2 x (20 + 15) = 70 Figuras Regulares CUBO a Para calcular el área y el volumen de un cubo que tenga A altura de 15, B base de 15 C profundidad de 15, se puede usar la siguiente fórmula: Área = 6 x L^2 c Volumen = L^3 b Donde L es la longitud de cualquiera de los lados del cubo. En este caso, L es igual a 15, ya que todos los lados son iguales. Por lo tanto, se tiene que: área = 6 x 15^2 Volumen = 15^3 área = 6 x 225 área= 1350 Volumen = 3375 El área y el volumen del cubo son 1350 y 3375, respectivamente. Descargado por Marsel Lobo (marselobo123@gmail.com) lOMoARcPSD|35117404 CILINDRO Para calcular el área total y el volumen de un cilindro con los siguientes datos, se puede usar la siguiente fórmula: h Área total = 2πr (r + h) Volumen = πr^2h r Donde r es el radio de la base, h es la altura del cilindro y π es una constante aproximada a 3.14. Sustituyendo los valores dados, se obtiene: Área total = 2 * 3.14 * 4 * (4 + 15) = 478.56 Volumen = 3.14 * 4^2 * 15 = 753.6 El área total del cilindro es de 478.56 unidades cuadradas y el volumen es de 753.6 unidades cúbicas. CONCLUSIÓN En conclusión, el trabajo de cálculo de áreas y volúmenes ha sido una actividad muy útil para aplicar los conceptos matemáticos aprendidos en clase. El documento de Excel nos ha permitido organizar los datos, realizar los cálculos y presentar los resultados de forma clara y precisa. Las fórmulas de Excel nos han facilitado el proceso de cálculo y nos han ahorrado tiempo y errores. Este trabajo nos ha mostrado la importancia de las matemáticas en la resolución de problemas reales y la utilidad de las herramientas informáticas para apoyar el aprendizaje. BIBLIOGRAFIA (1212) Cálculo de Área, Perímetro y Volumen en Excel - YouTube Cálculo de áreas y volúmenes. Fórmulas y Ejemplos (mundoestudiante.com) (1212) Perímetro, área y volumen - YouTube Descargado por Marsel Lobo (marselobo123@gmail.com)