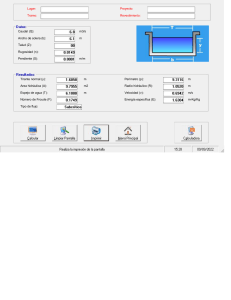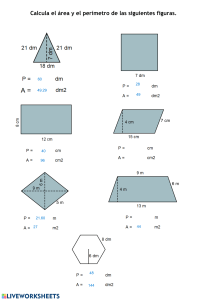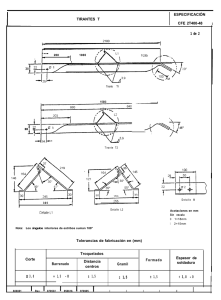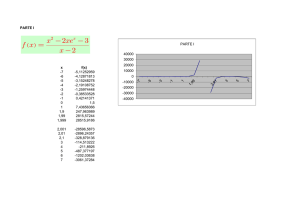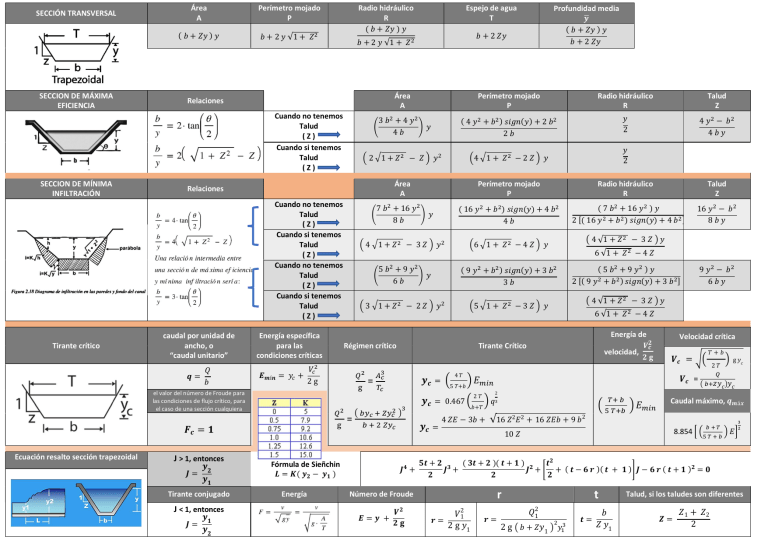
SECCIÓN TRANSVERSAL SECCION DE MÁXIMA EFICIENCIA Área A Perímetro mojado P ( 𝑏 + 𝑍𝑦 ) 𝑦 𝑏 + 2 𝑦 √1 + 𝑍 Radio hidráulico R ( 𝑏 + 𝑍𝑦 ) 𝑦 Área A Relaciones 3𝑏 +4𝑦 4𝑏 2 1+𝑍 Cuando no tenemos Talud (Z) Cuando si tenemos Talud (Z) Cuando no tenemos Talud (Z) Cuando si tenemos Talud (Z) Tirante crítico caudal por unidad de ancho, o “caudal unitario” Energía específica para las condiciones críticas 𝑄 𝒒= 𝑏 𝑉 𝑬𝒎í𝒏 = 𝑦 + 2g el valor del número de Froude para las condiciones de flujo crítico, para el caso de una sección cualquiera J > 1, entonces 𝒚 𝑱= 𝟐 𝒚𝟏 Tirante conjugado J < 1, entonces 𝒚 𝑱= 𝟏 𝒚𝟐 − 𝑍 Radio hidráulico R Talud Z ( 4 𝑦 + 𝑏 ) 𝑠𝑖𝑔𝑛(𝑦) + 2 𝑏 2𝑏 𝑦 2 4𝑦 − 𝑏 4𝑏𝑦 4 1+ 𝑍 −2𝑍 𝑦 2 𝑦 7 𝑏 + 16 𝑦 8𝑏 4 1+𝑍 𝑦 − 3𝑍 5𝑏 +9𝑦 6𝑏 3 1+𝑍 Radio hidráulico R Talud Z ( 16 𝑦 + 𝑏 ) 𝑠𝑖𝑔𝑛(𝑦) + 4 𝑏 4𝑏 ( 7 𝑏 + 16 𝑦 ) 𝑦 2 [( 16 𝑦 + 𝑏 ) 𝑠𝑖𝑔𝑛(𝑦) + 4 𝑏 ] 16 𝑦 − 𝑏 8𝑏𝑦 𝑦 6 1+ 𝑍 −4𝑍 𝑦 5 1+ 𝑍 −3𝑍 − 3𝑍 𝑦 6 √1 + 𝑍 − 4 𝑍 (5𝑏 +9𝑦 )𝑦 2 [( 9 𝑦 + 𝑏 ) 𝑠𝑖𝑔𝑛(𝑦) + 3 𝑏 ] 4 √1 + 𝑍 𝑦 Tirante Crítico = 4𝑇 𝒚𝒄 = 5 𝑇+𝑏 − 3𝑍 𝑦 𝒚𝒄 = Fórmula de Sieñchin 𝑳 = 𝑲( 𝒚𝟐 − 𝒚𝟏 ) 𝑱𝟒 + 𝑽𝟐 𝟐𝐠 𝟐𝐠 𝑽𝒄 = 2𝑇 𝑇+𝑏 𝑽𝒄 = 2 𝑞3 𝐸 2𝑇 g 𝑦𝑐 𝑦𝑐 𝑦𝑐 Caudal máximo, 𝒒𝒎á𝒙 4 𝑍𝐸 − 3𝑏 + √16 𝑍2 𝐸2 + 16 𝑍𝐸𝑏 + 9 𝑏2 8.854 10 𝑍 𝐸 𝟓𝒕 + 𝟐 𝟑 ( 𝟑𝒕 + 𝟐 )( 𝒕 + 𝟏 ) 𝟐 𝒕𝟐 𝑱 + 𝑱 + + ( 𝒕 − 𝟔 𝒓 )( 𝒕 + 𝟏 ) 𝑱 − 𝟔 𝒓 ( 𝒕 + 𝟏 )𝟐 = 𝟎 𝟐 𝟐 𝟐 r Número de Froude 𝑬=𝒚 + velocidad, Velocidad crítica 𝑽𝟐𝒄 𝐸 𝑏+𝑇 9𝑦 − 𝑏 6𝑏𝑦 6 √1 + 𝑍 − 4 𝑍 Energía de Régimen crítico = Energía 4 √1 + 𝑍 𝑦 ( 9 𝑦 + 𝑏 ) 𝑠𝑖𝑔𝑛(𝑦) + 3 𝑏 3𝑏 𝑦 − 2𝑍 𝑦 Perímetro mojado P 𝒚𝒄 = 0.467 𝑭𝒄 = 𝟏 Ecuación resalto sección trapezoidal 𝑦 Perímetro mojado P Área A Relaciones Profundidad media 𝒚 ( 𝑏 + 𝑍𝑦 ) 𝑦 𝑏 + 2 𝑍𝑦 𝑏 + 2 𝑍𝑦 𝑏 + 2 𝑦 √1 + 𝑍 Cuando no tenemos Talud (Z) Cuando si tenemos Talud (Z) SECCION DE MÍNIMA INFILTRACIÓN Espejo de agua T 𝒓= 𝑉21 2 g 𝑦1 𝒓= t 𝑄21 2 g 𝑏 + 𝑍 𝑦1 𝒕= 𝑦 𝑏 𝑍 𝑦1 Talud, si los taludes son diferentes 𝒁= 𝑍1 + 𝑍2 2 SECCIÓN RECTANGULAR SECCION DE MÁXIMA EFICIENCIA Tirante crítico Área A Perímetro mojado P 𝑏𝑦 𝑏+2𝑦 Relaciones caudal por unidad de ancho, o “caudal unitario” 𝒒= 𝑄 𝑏 el valor del número de Froude para las condiciones de flujo crítico, para el caso de una sección cualquiera Área A Energía específica para las condiciones críticas Radio hidráulico R 𝑏𝑦 𝑏+2𝑦 Espejo de agua T Profundidad media 𝒚 𝑏 𝑦 Perímetro mojado P Radio hidráulico R Energía de Régimen crítico Tirante Crítico Fórmula de Sieñchin 𝑳 = 𝑲( 𝒚𝟐 − 𝒚𝟏 ) velocidad, 𝑽𝟐𝒄 Talud Z Velocidad crítica 𝟐𝐠 2 = 𝒚𝒄 = 𝐸 2 𝑽𝟐𝒄 𝒚𝒄 = 0.467 𝑞3 𝟐𝐠 3 = 𝐸𝑚𝑖𝑛 Caudal máximo, 𝒒𝒎á𝒙 =𝑏 𝑦 1.704 𝐸 𝑭𝒄 = 𝟏 Ecuación resalto sección Rectangular Espejo de agua T Energía Número de Froude 𝑬=𝒚 + 𝑽𝟐 𝟐𝐠 Número de Froude Talud, si los taludes son diferentes SECCIÓN TRIANGULAR SECCION DE MÁXIMA EFICIENCIA Tirante crítico Área A Perímetro mojado P 𝑍𝑦 2 𝑦 √1 + 𝑍 Relaciones caudal por unidad de ancho, o “caudal unitario” Radio hidráulico R 𝑍𝑦 Profundidad media 𝒚 𝑦 2 2 𝑍𝑦 2 √1 + 𝑍 Área A Energía específica para las condiciones críticas Espejo de agua T Perímetro mojado P Radio hidráulico R Régimen crítico Tirante Crítico Espejo de agua T Profundidad media 𝒚 Energía de Velocidad crítica velocidad, 𝑄 𝒒= 𝑏 el valor del número de Froude para las condiciones de flujo crítico, para el caso de una sección cualquiera 𝑉 𝑬𝒎í𝒏 = 𝑦 + 2g J > 1, entonces 𝒚 𝑱= 𝟐 𝒚𝟏 Tirante conjugado J < 1, entonces 𝒚 𝑱= 𝟏 𝒚𝟐 𝟐𝐠 𝑽𝒄 = 𝟎. 𝟕𝟎𝟕 g 𝑦 Caudal máximo, 𝒒𝒎á𝒙 2 𝒚𝒄 = 0.935𝑞3 = 𝑭𝒄 = 𝟏 Ecuación resalto sección triangular = 𝑽𝟐𝒄 0.792 𝐸 Fórmula de Sieñchin 𝑳 = 𝑲( 𝒚𝟐 − 𝒚𝟏 ) Energía 𝑱𝟒 + 𝑱𝟑 + 𝑱𝟐 − 𝟔 𝒓( 𝑱 + 𝟏 ) = 𝟎 r Número de Froude 𝑬=𝒚 + 𝑽𝟐 𝟐𝐠 𝒓= 𝑉21 2 g 𝑦1 𝒓= t 𝑄21 2g𝑍 𝑦 𝒕= 0 Talud, si los taludes son diferentes 𝒁= 𝑍1 + 𝑍2 2 Área A SECCIÓN CIRCULAR Perímetro mojado P 1 ( 𝜃 − 𝑠𝑒𝑛𝜃 ) 𝐷 8 𝜃 = 2 𝑐𝑜𝑠 SECCION DE MÁXIMA EFICIENCIA Tirante crítico 1− 1 𝑠𝑒𝑛𝜃 1− 4 𝜃 Espejo de agua T 2 𝑦( 𝐷 − 𝑦 ) 𝐷 𝑠𝑒𝑛 1 𝜃 𝐷 2 2𝑦 𝐷 Relaciones caudal por unidad de ancho, o “caudal unitario” 𝒒= 1 𝜃𝐷 2 Radio hidráulico R Área A Energía específica para las condiciones críticas Perímetro mojado P Régimen crítico 𝑄 𝑏 el valor del número de Froude para las condiciones de flujo crítico, para el caso de una sección cualquiera 𝑬𝒎í𝒏 = 𝑦 + 𝑉 2g = 𝑭𝒄 = 𝟏 Ecuación resalto sección triangular Fórmula de Sieñchin 𝑳 = 𝑲( 𝒚𝟐 − 𝒚𝟏 ) Energía Número de Froude 𝑬=𝒚 + 𝑽𝟐 𝟐𝐠 Radio hidráulico R Tirante Crítico Espejo de agua T Profundidad media 𝒚 SECCIÓN PARABÓLICA Área A SECCION DE MÁXIMA EFICIENCIA Relaciones Área A Perímetro mojado P Radio hidráulico R Espejo de agua T Profundidad media 𝒚 𝑻 = 2 √2 𝑦 𝟒 √2 𝑦 𝟑 𝟖 √2 𝑦 𝟑 𝟏 𝑦 𝟐 2 √2 𝑦 𝟐 √2 𝑦 𝟑 caudal por unidad de ancho, o “caudal unitario” Energía específica para las condiciones críticas Tirante crítico Perímetro mojado P Radio hidráulico R Espejo de agua T Energía de Régimen crítico Tirante Crítico 3 𝒒= 𝒚𝒄 = 𝐸 𝑄 𝑏 el valor del número de Froude para las condiciones de flujo crítico, para el caso de una sección cualquiera 4 2 𝑬𝒎í𝒏 = 𝑦 + 𝑉 2g 𝒚𝒄 = 0.701 𝑞3 = 𝑭𝒄 = 𝟏 Ecuación resalto sección triangular J > 1, entonces 𝒚 𝑱= 𝟐 𝒚𝟏 Tirante conjugado J < 1, entonces 𝒚 𝑱= 𝟏 𝒚𝟐 Fórmula de Sieñchin 𝑳 = 𝑲( 𝒚𝟐 − 𝒚𝟏 ) Energía Número de Froude 𝑬=𝒚 + 𝑽𝟐 𝟐𝐠 velocidad, 𝑽𝟐𝒄 𝟐𝐠 Velocidad crítica