Introducción a Machine Learning

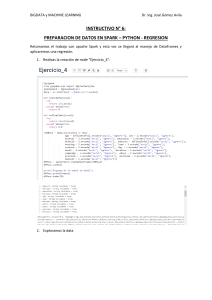
INTRODUCCIÓN A
MACHINE LEARNING
Mg. Heber Baldeón Paucar
heberjbaldeon@gmail.com
Análisis de Datos y
Econometría Aplicada con R
Índice
I. Machine Learning
II. Aprendizaje supervisado
1.
2.
3.
Decision trees y Randon Forest
Red Neuronales Artificiales
a. Gradiente decreciente
b. Algoritmo de aprendizaje (Función de activación sigmoidal y Backpropagation)
Suport Vector Machine (SVM o SVR)
III. Aprendizaje no supervisado
1.
2.
Clustering:
a. K means
b. Fuzzy c means
Reducción de dimensionalidad
a. Principal Component Analysis (PCA)
IV. Cross Validation
Data Science
Jim Gray, ganador del premio Turing en 1998, imaginó la ciencia de datos como un "cuarto
paradigma" de la ciencia (empírico, teórico, computacional y ahora basado en datos).
Data Science
Fuente: https://towardsdatascience.com/the-mathematics-of-machine-learning-894f046c568
I. Machine Learning
 Minería de datos: Proceso de extraer
conocimiento útil y comprensible,
previamente desconocido, desde grandes
cantidades de datos almacenados en
distintos formatos.
•
Machine learning permite a las
computadoras hacer lo que las
personas y animales hacen
naturalmente: aprender de la
experiencia.
•
Los algoritmos de Machine learning
usan los métodos computacionales
para “aprender” directamente de la
data sin depender de ninguna ecuación
predeterminada como un modelo.
•
Estos algoritmos mejoran su
performance cuando la muestra
disponible para el aprendizaje
aumenta.
I. Machine Learning
Fuente: https://towardsdatascience.com/coding-deep-learning-for-beginners-types-of-machine-learning-b9e651e1ed9d
I. Machine Learning
•
•
•
Machine learning usa 2 tipos de técnicas:
Aprendizaje supervisado (Supervised
learning), cuando entrenas un modelo
conociendo los inputs y outputs, por lo que
puedes hacer proyecciones sobre los
outputs, y
El entrenamiento excesivo origina la
memorización, la red deja de generalizar y
empieza a reproducir, sólo funciona bien
para los datos del entrenamiento, pero si
pruebo con otros no.
Aprendizaje no supervisado (Unsupervised
learning), cuando encuentras patrones
escondidos o estructuras intrínsecas solo con
inputs y sin conocer los outputs.
I. Machine Learning
II. Aprendizaje supervisado
•
•
Las técnicas de clasificación predicen
respuestas discretas —por ejemplo, si un
email es spam o no, o si un tumor es
benigno o maligno. Los modelos de
clasificación son entrenados para clasificar
datos en categorías. Aplicaciones incluyen
reconocimiento de imágenes médicas,
reconocimiento de discursos y credit
scoring.
Las técnicas de regresión predicen
respuestas continuas — por ejemplo,
cambios de temperatura o fluctuaciones de
la demanda de electricidad. Aplicaciones
incluyen forecasting stock prices,
reconocimiento de escritura a mano, y
procesamiento de señales acústicas.

Seleccionar un algoritmo de machine
learning es un proceso de ensayo y error.

Existe un trade-off entre las
características específicas de los
algoritmos, como:
 Velocidad de aprendizaje
 Uso de memoria
 Precisión predictiva en nueva data
 Transparencia e interpretabilidad
(cuan fácilmente se puede entender
la razón de las predicciones que hace
el algoritmo)
II. Aprendizaje supervisado
Regresión lineal: Las regresiones lineales son técnicas
estadísticas usadas para describir respuestas de
variables continuas como una función lineal de una o
más predictores. Como los modelos de regresión
lineal son los más simples de interpretar y de
entrenar.


Cuando necesitas un algoritmo fácil de interpretar y
rápido de estimar (fittear)
Como línea de base para evaluar otros modelos más
complejos
Support Vector Regression (SVR): Los algoritmos de
regresiones SVR encuentran un modelo que se desvía
de los datos medios por un valor pequeña, con valores
de parámetro que son tan pequeños como sea posible
(para minimizar la sensibilidad al error)

Para datos de alta dimensión (donde habrá un gran
número de variables predictoras)
II. Aprendizaje supervisado
Redes neuronales. Inspirado en el cerebro humano, una red
neuronal consiste en redes altamente conectadas de neuronas
que relacionan las entradas con las salidas deseadas. La red se
entrena modificando iterativamente las fuerzas de las
conexiones de modo que las entradas dadas se correspondan
con la respuesta correcta.
– Para modelar sistemas altamente no lineales o cuando podría haber
cambios inesperados en sus datos de entrada
– Cuando los datos están disponibles incrementalmente y desea
actualizar constantemente el modelo y la interpretabilidad del
modelo no es una preocupación clave
Regression Tree: Hay Decision Trees para clasificación y
Decision Tree para regresiones y son utilizadas para predecir
respuestas continuas.
 Cuando el predictor es categórica (discreta) o un
comportamiento no lineal
II. Aprendizaje supervisado
Decision Tree
 Particiones
 Excluyente
 Colectivamente exhaustivas
 Criterios para la selección de
particiones
𝐼 𝑠 = ෍ 𝑝𝑗 . 𝑓 𝑝𝑗1 , 𝑝𝑗2 , … , 𝑝𝑗𝑐
𝑗=1..𝑛
Criterios:
 Error esperado.
 Gini
 Entropía
 DKM
II. Aprendizaje supervisado
•
Decision Tree
¿Astigmatismo?
sí
no
NO
NO
¿Miopía?
¿Edad?
≤ 𝟐𝟓
> 𝟓𝟎
NO
NO
> 𝟐𝟓 𝒚 ≤ 𝟓𝟎
¿Miopía?
¿Miopía?
¿Miopía?
¿Miopía?
¿Miopía?
SÍ
¿Miopía?
¿Miopía?
NO
NO
¿Miopía?
¿Miopía?
¿Miopía?
> 𝟏, 𝟓 𝒚 ≤ 𝟏𝟎
NO
>𝟔
¿Miopía?
> 𝟏𝟎
≤ 𝟏, 𝟓
≤𝟔
NO
¿Miopía?
¿Miopía?
¿Miopía?
¿Miopía?
II. Redes Neuronales Artificiales (RNA)
Las Redes Neuronales Artificiales (RNA) son técnicas matemático – computacionales inspirados en el
funcionamiento del cerebro humano (almacena la información en forma de patrones y utiliza estos para
resolver problemas).
Usos: Reconocimiento de patrones, la comprensión de información y la reducción de dimensionalidad, el
agrupamiento, la clasificación, la visualización, predicción, etc.
II. Redes Neuronales Artificiales (RNA)
Problema OR
Distintas formas de las regiones generadas por
un perceptrón multinivel
Perceptrón Multicapa
II. Redes Neuronales Artificiales (RNA)
(2)
(1)
(1)
(1)
(1)
(2)
(1)
(1)
(1)
(1)
(2)
(1)
(1)
(1)
(1)
𝑎1 = 𝑔 𝜃10 𝑥0 + 𝜃11 𝑥1 +𝜃12 𝑥2 + 𝜃13 𝑥3
𝑎2 = 𝑔 𝜃20 𝑥0 + 𝜃21 𝑥1 +𝜃22 𝑥2 + 𝜃23 𝑥3
𝑎3 = 𝑔 𝜃30 𝑥0 + 𝜃31 𝑥1 +𝜃32 𝑥2 + 𝜃33 𝑥3
(3)
(2) (2)
(1)
(1)
(2) (2)
(2) (2)
(3) (2)
ℎ𝜃 𝑥 = 𝑎1 = 𝑔 𝜃10 𝑎0 + 𝜃11 𝑎1 + 𝜃12 𝑎2 + 𝜃13 𝑎3
(2)
𝑧1
(1)
(1)
= 𝜃10 𝑥0 + 𝜃11 𝑥1 + 𝜃12 𝑥2 + 𝜃13 𝑥3
(2)
(1)
(1)
(1)
(1)
𝑧2 = 𝜃20 𝑥0 + 𝜃21 𝑥1 + 𝜃22 𝑥2 + 𝜃23 𝑥3
(2)
(1)
(1)
(1)
𝑥0
𝑥1
𝑥= 𝑥
2
𝑥3
2
𝑧1
⋀ 𝑧 2 = 𝑧22
⋀ 𝑎 2 = 𝑔(𝑧 2 )
2
𝑧2
(1)
𝑧3 = 𝜃30 𝑥0 + 𝜃31 𝑥1 + 𝜃32 𝑥2 + 𝜃33 𝑥3
𝑧 (3) = ℎ𝜃 𝑥 = 𝑎(3) = Ɵ(2) 𝑎(2)
II. Redes Neuronales Artificiales (RNA)
La función de activación
define el nuevo estado o
la salida de la neurona
en términos del nivel de
excitación de la misma.
II. Redes Neuronales Artificiales (RNA)
𝑋Ɵ(1) = 𝑍 (2)
𝑎(2) = 𝑓(𝑍 (2) )
𝑎(3) = 𝑎(2) Ɵ(2)
𝑌෠ = 𝑓(𝑎 3 )
3
𝐽=
𝜃21
1
𝜃31
1
𝜃22
1
𝜃32
𝜃12
𝜃10
1
Ɵ 1 = 𝜃111
1
1
𝛿𝜃30
𝛿𝐽
1
𝛿𝜃31
, Ɵ2 =
𝛿𝜃21
𝛿𝐽
1
𝛿𝜃22
1
2
𝜃30
1
𝛿𝐽
𝑛=1
1
𝛿𝜃20
𝛿𝐽
𝛿𝜃20
3
𝜃20
1
1
𝑛=1
1
2
𝐽 = ෍ 𝑦 − 𝑓(𝑓(𝑋Ɵ 1 )Ɵ 2 )
2
1
𝛿𝐽
𝜕𝐽
=
1
𝛿𝜃11
𝜕Ɵ 1
𝛿𝐽
1
1
෍ (𝑦 − 𝑦)
ො 2 = ෍ (𝑒𝑛 )2
2
2
𝜃10
𝛿𝐽
𝛿𝜃10
𝛿𝐽
3
𝑛=1
𝛿𝐽
2
𝜃11
2
𝜃12
2
𝜃13
𝛿𝜃10
𝛿𝐽
1
𝜕𝐽
𝛿𝜃11
=
𝛿𝐽
𝜕Ɵ 2
1
𝛿𝜃12
𝛿𝐽
1
𝛿𝜃13
1
1
𝛿𝐽
1
𝛿𝜃32
II. Redes Neuronales Artificiales (RNA)
1
1
𝜕 σ 𝑦 − 𝑦ො 2
𝜕 𝑦 − 𝑦ො 2
𝜕𝐽
2
2
=
=
෍
𝜕Ɵ 2
𝜕Ɵ 2
𝜕Ɵ 2
𝜕𝐽
𝜕𝑦ො 𝜕𝑧 3
= −(𝑦 − 𝑦)
ො
𝜕Ɵ 2
𝜕𝑧 3 𝜕Ɵ 2
3
𝛿𝐽
𝜕𝑧
3
=
−(𝑦
−
𝑦)𝑓′(𝑧
ො
)
𝛿Ɵ 2
𝜕Ɵ 2
− 𝑦 − 𝑦ො 𝑓 ′ 𝑧 3
=𝛿3
𝜕𝐽
𝜕𝑧 3
3
=𝛿
𝜕Ɵ 2
𝜕Ɵ 2
2
𝑎11
𝜕𝑧 (3)
2
=
𝑎
21
𝜕Ɵ 2
2
𝑎31
2
𝑎11
𝜕𝐽
= 𝑎122
2
𝜕Ɵ
2
𝑎13
2
𝑎12
2
𝑎13
𝑎22
2
𝑎23
2
𝑎33
2
2
𝑎32
2
𝑎21
2
𝑎31
𝑎22
2
𝑎32
2
𝑎33
𝑎23
2
2
𝜕𝐽
(2) 𝑇 (3)
=
𝑎
𝛿
𝜕Ɵ 2
𝛿 (3)
II. Redes Neuronales Artificiales (RNA)
1
1
𝜕 σ 𝑦 − 𝑦ො 2
𝜕 𝑦 − 𝑦ො 2
𝜕𝐽
2
2
=
=
෍
𝜕Ɵ 1
𝜕Ɵ 1
𝜕Ɵ 1
𝜕𝐽
𝜕𝑦ො 𝜕𝑧 3
= −(𝑦 − 𝑦)
ො
𝜕Ɵ 1
𝜕𝑧 3 𝜕Ɵ 1
3
𝛿𝐽
𝜕𝑧
3
= −(𝑦 − 𝑦)𝑓′(𝑧
ො
)
1
𝛿Ɵ
𝜕Ɵ 1
𝜕𝐽
𝜕𝑧 3
3
=𝛿
𝜕Ɵ 1
𝜕Ɵ 1
𝜕𝐽
𝜕𝑧 3 𝜕𝑎 2
3
=𝛿
𝜕Ɵ 1
𝜕𝑎 2 𝜕Ɵ 1
𝜕𝐽
=𝛿3 Ɵ2
1
𝜕Ɵ
𝑇 𝜕𝑎
2
𝜕Ɵ 1
𝜕𝐽
𝜕𝑎 2 𝜕𝑧 2
(3)
2 𝑇
= 𝛿 (Ɵ )
𝜕Ɵ 1
𝜕𝑧 2 𝜕Ɵ 1
𝛿𝐽
𝜕𝑧 2
(3)
2 𝑇
2
= 𝛿 (Ɵ ) 𝑓′(𝑧 )
𝛿Ɵ 1
𝜕Ɵ 1
𝜕𝐽
= 𝑋 𝑇 𝛿 (3) (Ɵ 2 )𝑇 𝑓′(𝑧 2 )
1
𝜕Ɵ
1
1
Ɵ𝑛𝑒𝑤 = Ɵ𝑜𝑙𝑑 − 𝜆
2
2
Ɵ𝑛𝑒𝑤 = Ɵ𝑜𝑙𝑑 − 𝜆
𝜕𝐽
𝜕Ɵ 1
𝜕𝐽
𝜕Ɵ 2
II. Redes Neuronales Artificiales (RNA)
Fuente: https://towardsdatascience.com/the-mostly-complete-chart-of-neural-networks-explained-3fb6f2367464
II. Support Vector Machine
SVM: Es una técnica de clasificación que resuelve un problema de optimización restringida.
Ventajas: Es una técnica de clasificación muy útil trabajando con datos multidimensionales. Trabaja
muy bien con pequeñas muestras.
Desventajas: Elegir los parámetros y kernels adecuados pueden ser computacionalmente intenso.
II. Support Vector Machine
¿Qué es SVM? Se trata de encontrar un hiperplane que maximiza los margin.
¿Por qué es una optimización restringida? Porque los support vectors no pueden ubicarse dentro del margin.
¿Cómo se resuelve - maximiza el margin? Utilizando la técnica de multiplicadores de Lagrange.
II. Support Vector Machine
II. Support Vector Machine
¿Qué es el parámetro C? Es el parámetro de penalización por los errores que se comenten.
¿Cuál es el valor de C? El parámetro C te permite decidir cuánto se quiere penalizar un punto mal clasificado.
II. Support Vector Machine
III. Aprendizaje no supervisado
k-Means: Particiones de datos en k número de
clústeres mutuamente excluyentes. Qué tan
bien fittea los puntos en un grupo se determina
por la distancia desde ese punto al centro del
cluster.
–
–
Cuando se conoce el número de clusters
Para agrupar rápidamente grandes
conjuntos de datos
Fuzzy c-Means: Clúster basado en particiones
cuando los puntos de datos pueden pertenecer
a más de un clúster.
Cuando se conoce el número de clusters
 Para el reconocimiento de patrones
 Cuando los grupos se superponen

III. Aprendizaje no supervisado
Self-Organizing Map: Clúster basado en redes neuronal
que transforma un conjunto de datos en un mapa 2D
que preserva la topología.
–
–
Para visualizar datos bidimensionales en 2D o 3D
Reducir la dimensionalidad de los datos
conservando su topología (forma)
Gaussian Mixture Model: Clúster basado en particiones
donde los puntos de datos provienen de diferentes
distribuciones normales multivariadas con ciertas
probabilidades.
Cuando un punto de datos puede pertenecer a
más de un clúster
 Cuando los clústeres tienen diferentes tamaños y
estructuras de correlación dentro de ellos

IV. Medidas de performance del forecast
Mean error forescast error (MFE)
𝑛
1
෍ 𝑥𝑡 − 𝑓𝑡
𝑛
Mean squared error (MSE)
𝑛
1
෍ 𝑥𝑡 − 𝑓𝑡 2
𝑛
•
•
𝑡=1
Un buen modelo tiene un MFE cercano
a 0.
– Provee la dirección de error.
– MFE=0 no garantiza que la
proyección no contenga error.
– Sensible a transformaciones de la
data y escala.
– No penaliza los errores extremos.
𝑡=1
Un buen modelo tiene un MSE cercano a 0.
– Muestra una idea general del error.
– Se enfatiza que el error total de
forecast es mas afectado por los
errores individuales grandes.
– Sensible a transformaciones de la data
y escala.
– Penaliza los errores extremos.
IV. Medidas de performance del forecast
Normalized Mean squared error (NMSE)
𝑛
1
෍ 𝑥𝑡 − 𝑓𝑡 2
2
𝜎 𝑛
•
U de Theil
𝑈=
𝑡=1
Un menor NMSE implica un mejor
forecast.
– Es una medida de error
balanceada.
– Es efectivo para evaluar la
precisión del forecast de un
modelo.
Coeficiente de determinación (R2)
σ𝑛𝑡=1 𝑥𝑡 − 𝑓𝑡 2
2
𝑅 = 1− 𝑛
σ𝑡=1 𝑥𝑡 − 𝑥ҧ 2
•
1 𝑛
σ𝑡=1 𝑥𝑡 − 𝑓𝑡 2
𝑛
1 𝑛
1 𝑛
σ𝑡=1 𝑓𝑡 2
σ
𝑥 2
𝑛
𝑛 𝑡=1 𝑡
Un buen forecast implica que la U de Theil sea
cercana a 0.
– Es una medida de error total
normalizada.
– 0 ≤ 𝑈 ≤ 1.
– U=0, significa ajuste perfecto.
IV. ¿Cuáles son las características de un buen estimador?
V. Validación cruzada
Fuente: https://es.wikipedia.org/wiki/Validaci%C3%B3n_cruzada
V. Validación cruzada de K iteraciones (folk)
Fuente: https://es.wikipedia.org/wiki/Validaci%C3%B3n_cruzada
V. Validación cruzada aleatoria
Fuente: https://es.wikipedia.org/wiki/Validaci%C3%B3n_cruzada
V. Validación cruzada dejando uno fuera
Fuente: https://es.wikipedia.org/wiki/Validaci%C3%B3n_cruzada