Formulas prob 084158 140509 2504
Anuncio
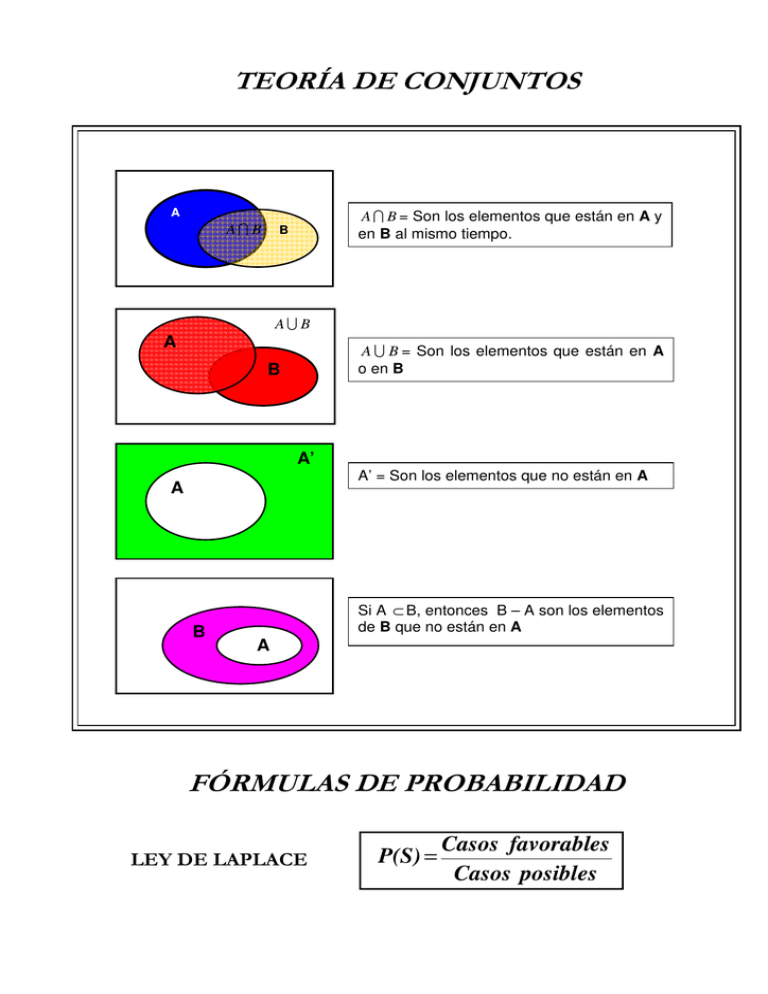
A A B A B = Son los elementos que están en A y en B al mismo tiempo. B A A B A B = Son los elementos que están en A o en B B A’ A B A A’ = Son los elementos que no están en A Si A ⊂ B, entonces B – A son los elementos de B que no están en A P(S) = Casos favorables Casos posibles - Complement ario : P(A) + P(A´) = 1 - Unión : P(A B) = P(A) + P(B) - P(A B) - Diferencia : A ⊂ B P(B - A) = P(B) - P(A) - A y B son independientes ⇔ P(A B) = P(A)·P(B) (Probabilidad de que ocurra A si ha ocurrido B) P(A/ B) = P(A B) P(B) (También se puede hacer fácilmente en forma de árbol) P(S) = P(A )·P(S / A ) + P(A )·P(S / A ) + ...+ P(An )·P(S / An ) 1 1 2 2 (Esta fórmula se saca de las dos anteriores y también es útil el desarrollo en árbol) P(Ai / S) = P(Ai )·P(S/Ai ) P(A1 )·P(S / A1 ) + ....+ P(An)·P(S / An )









![Adaptation of the PSS (14 items) for Mexico [in Spanish] Marca la](http://s2.studylib.es/store/data/006612558_1-29f96c224c6c50514455f083244b1685-300x300.png)
