FUNCI N DE ESTRUCTURA DE ALEACIONES BINARIAS

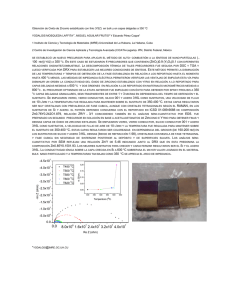
CONGRESO CONAMET/ SAM 2004
FUNCIÓN DE ESTRUCTURA DE ALEACIONES BINARIAS
H. De Cicco y J. Ovejero García
Departamento Materiales, Comisión Nacional de Energía Atómica, Av. General Paz 1499, (B1650KNA) San
Martín, Buenos Aires, Argentina. decicco@cnea.gov.ar
RESUMEN
Se presenta una simulación montecarlo del crecimiento de una fase rica en un elemento en una aleación binaria
AB, analizado por medio de la evolución de la función de estructura. Una simulación montecarlo resulta
adecuada dado que el problema de difusión de átomos de una región a otra del espacio es homólogo a un modelo
de Ising, para el cual espines 1 o –1 representan átomos de la especie A o B. La diferencia con un Ising usual,
reside en la circunstancia de que en un problema de difusión debe conservarse la cantidad de materia, es decir en
lenguaje de espines, la magnetización debe permanecer constante a lo largo del tiempo montecarlo. Este
requisito impone que un espin 1, por ejemplo, sólo pueda intercambiarse con un espin vecino –1.
Palabras claves: Montecarlo, crecimiento de Ostwald.
1. INTRODUCCIÓN TEÓRICA
El problema de la evolución en el tiempo de la
composición en una aleación binaria AB, cuando es
enfriada a una temperatura debajo de la temperatura
crítica de la campana de miscibilidad, ha sido
investigado intensamente, debido su relevancia en
nivel básico y práctico[1-9].
A alta temperatura no existe ninguna correlación en la
composición del sistema en diferentes posiciones r,
con lo cual la función de estructura del sistema, S(k),
la cual se obtiene experimentalmente mediante
dispersión de neutrones, es esencialmente cero. Los
valores de los campos de concentración, nA(r) y nB(r),
corresponden a los valores medios nA y nB ,
independientes de r.
En temperaturas debajo de la Tc, existen gamas de
concentraciones en los cuales el equilibrio del sistema
consta de dos fases, una rica en A y la otra rica en B.
Un esta región del diagrama de fases existen
correlaciones espaciales en las composiciones de A y
B. Si se define n(r)=nA(r)-nB(r)/nA+nB,, n(r)∈[-1,1].
En la curva de coexistencia se tiene nA,y nB,
evidentemente. La función de estructura revelará la
existencia de estas fases.
En el tiempo el sistema evolucionará hacia su estado
de equilibrio de acuerdo a una cinética que ha sido
descrita originalmente en trabajos de Lifshitz, Slyozov
y Wagner, Hillert, Cahn y Hillard [1,2-6] . Toda la
teoría descansa en la asunción de cierta energía libre F
del sistema, la cual es una adaptación de la energía
libre empleada por Guinzburg y Landau en su teoría
de la superconductividad, el cual también es un
fenómeno de temperatura crítica [10].
[
]
F = ∫ f (r ) − K (∇ 2 n) 2 dr , (1)
donde f(r) representa la energía libre de la mezcla
homogénea.
La teoría basada en (1) en acuerdo con lo observado
experimentalmente, muestra un crecimiento de fase de
cierta longitud característica l ≈ t1/3 [1] y una
distribución de precipitados que favorece el
crecimiento de los de mayor tamaño, con lo cual se
disminuye la energía de interfase matrizprecipitado(se asume fracción en volumen constante).
Ciertamente la constante K en (1) representa una
energía o tensión superficial tal como aquella que se
encuentra en la formación de burbujas de vapor en el
seno de un líquido. El fenómeno descrito es lo que se
conoce en la literatura como crecimiento de Ostwald
[1].
El presente trabajo consiste en una simulación
montecarlo del crecimiento de una fase rica en un
elemento en una aleación binaria AB. Una simulación
montecarlo resulta adecuada dado que el problema de
difusión de átomos de una región a otra del espacio es
homólogo a un modelo de Ising, para el cual espines 1
o –1 representan átomos de la especie A o B. La
diferencia con un Ising usual, reside en la
circunstancia de que en un problema de difusión debe
conservarse la cantidad de materia, es decir en
lenguaje de espines, la magnetización debe
permanecer constante a lo largo del tiempo montecarlo
[11]. Este requisito impone que un espin 1, por
ejemplo, sólo pueda intercambiarse con un espin
vecino –1.
CONGRESO CONAMET/ SAM 2004
El hamiltoniano, que da la probabilidad con la que se
recorre el espacio de fases, es el típico hamiltoniano
de Ising [12-15]:
H = − J ∑i , j n i n j ,
S (k , t ) = N −1 ∑ eikr g (r , t ) , (6)
con N el número de espines y k el vector de onda, que
en una transformada discreta es: k = 2πμ / N , con
(2)
μ=0,1,2,... N .
donde la suma es sobre primeros vecinos y J>0 mide
la intensidad de la interacción en unidades de kT.
Para el cálculo se empleó una malla bidimensional de
3600 espines, con condiciones de contorno periódicas
La concentración inicial es 0.5, es decir el valor
medio η =0 y se investigaron distintas temperaturas.
Un comentario acerca del tiempo montecarlo es
pertinente, ya que cuando se desea hacer una
simulación que arroje como resultado una evolución
temporal, lo usual es hacer dinámica molecular y no
un cálculo montecarlo. Aquí reside otra diferencia con
un montecarlo usual. En primer lugar, todos los
promedios que se hacen en una corrida , en nuestro
caso se llevan a cabo sobre diferentes corridas, con
condiciones iniciales evidentemente diferentes. En
segundo lugar se requiere adoptar un criterio acerca de
que se entiende por tiempo en cada simulación. El
intercambio de espines vecinos de distinto signo que
representa intercambiar un átomo A con otro B debe
cumplir la conocida ley de difusión:
l 2 ≈ Dt ,
En realidad lo que se calcula es la función de
estructura (6) promediada circularmente es decir [12]:
(2π / N )( μ − 1 / 2) ≤ k ≤ ( 2π / N )( μ + 1 / 2) .
Un sistema como el investigado tendrá un gap de
miscibilidad dentro del cual se halla una curva de
equilibrio metaestable, la llamada espinodal, la cual
puede obtenerse de los puntos de inflexión de la
energía libre suponiendo solución regular (Fig.1).
La temperatura crítica indicada en la figura 1 es
Tc=2.27J/kB , de acuerdo con Onsager para un Ising
bidimensional, o sea se tiene un βc=0.44.
1,2
1,0
0,8
T/Tc
0,6
0,4
Espinodal
0,2
(3)
0,0
-1,0
donde l es el camino libre medio y D el coeficiente de
difusión. En un intercambio de primeros vecinos l
debe ser del orden del parámetro de red a. Además en
una malla dimensional se tiene 4 primeros vecinos
con lo cual la unidad de tiempo de todas las
simulaciones puede escribirse:
α (T ) = 4 D (T ) / a
(4)
Además de lo anterior se requiere asumir cuántos
intercambios de espines se dan simultáneamente en la
unidad de tiempo en distintos sitios de la red. En todos
los cálculos llevados a cabo se ha asumido que en la
unidad de tiempo (4) se dan 1800 intercambios de
espines, es decir se mueve la mitad de los espines
considerados, pero debe enfatizarse que esta elección
es arbitraria y toda comparación posterior con
resultados experimentales deberá partir de algún tipo
de calibración del eje temporal.
La cantidad primaria a evaluar y sus promedios
evaluados en diferentes corridas es la función de
correlación atómica g(r,t) definida en la forma usual:
(
)(
g ( r , t ) = n ( r´, t ) − n n ( r´+ r , t ) − n
)
-0,5
0,0
0,5
1,0
n
Figura 1 Esquema del diagrama de fases de la
aleación estudiada
2. RESULTADOS
En las figuras siguientes se muestran resultados de
simulaciones en dos temperaturas: 0,5β y 0,8β, para
los primeros instantes (Fig.2) tras el enfriamiento
dentro del gap de miscibilidad y para tiempos largos
(Fig.3a-b) Cada punto representa el promedio de 8
simulaciones independientes.
8
7
μ=5 β=0.5
6
5
S(k,t)
4
3
(5)
2
1
Como se señaló en otro lugar, uno observa la función
de correlación “iluminando” el material con, por
ejemplo neutrones, o sea aplica expi(wt –kr), con lo
cual transforma Fourier (5) y obtiene la función de
estructura S(k,t):
0
-10000
0
10000
20000
30000
40000
50000
-1
tα
Figura 2 Resultado de 8 simulaciones independientes de
los primeros instantes tras el enfriamiento para β=0,5.
CONGRESO CONAMET/ SAM 2004
decir un incremento de la longitud de onda
mayormente dispersada, será reflejado como un
desplazamiento del máximo de la función de
estructura hacia valores menores del vector k, lo cual
puede observarse cualitativamente en las figuras 5 y 6.
μ
120
β =0.8
2
100
80
60
S(k,t)
3
40
1
20
4
5
6
7
0
0.0
5
6
6
6
6
5.0x10 1.0x10 1.5x10 2.0x10 2.5x10 3.0x10
6
t
Figura 3a Evolución de la función de estructura
para β=0,8 y μ=1-7
70
β =0.5
μ =2
60
50
40
S(k,t)
μ =1
30
μ=3
Figura 4 Instante inicial y final de la evolución de la
mezcla AB tras 2x106 intercambios. a β=0.5.
20
μ =4
10
μ =5
μ =6
μ=7
0
0.0
5
6
6
6
6
6
6
5.0x10 1.0x10 1.5x10 2.0x10 2.5x10 3.0x10 3.5x10
tα
-1
Figura.3b Evolución de la función de estructura
para β=0,5 y μ=1-7
En la figura 4 se observa el instante inicial de la
mezcla homogénea y el estado final fuertemente
correlacionado tras 2x106 intercambios de espines a
β=0.5. Se evidencia claramente la segregación de una
fase rica en uno de los elementos, indistinta acerca de
cual es este ya que habíamos partido de una mezcla
con la misma cantidad de A y B.
La segregación y expansión de las nuevas fases a lo
largo del tiempo debe verse reflejada en la función de
estructura a distintos tiempos. Es de esperar que las
longitudes de onda λ del haz de neutrones cuyos
valores están cercanos a los tamaños de los dominios
de fase segregada contribuyan predominantemente a la
función de estructura. Teniendo en cuenta que k=2π/λ,
un crecimiento de fase segregada en el tiempo, es
La posibilidad de cuantificar el observado crecimiento
de Ostwald requiere una malla de mayor tamaño para
reducir la dispersión hallada. Por otra parte, y esto es
algo que se observa claramente en (
), se tiene percolación en la concentración estudiada lo
cual hace difícil cualquier estimación de la evolución
de cierta dimensión característica de la fase segregada.
Un estudio más revelador implicará entonces el
empleo de mallas de mayor número de espines y
concentraciones iniciales cercanas a la zona rica en A
30
t=426000
25
20
β =0,8
t=324000
S(k,t) 15
10
t=201600
t=100800
5
0
t=32400
t=0
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
k
Figura 5 Evolución de la función de estructura con k
para distintos tiempos en β=0.8
CONGRESO CONAMET/ SAM 2004
o B según el diagrama de la figura 1.
4. REFERENCIAS
50
t=664200
40
30
S(k,t)
t=401400
20
t=300600
10
t=201600
t=100800
t=50400
t=0
0
β =0,5
t=500400
-0.4 -0.2 0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
k
Figura 6 Evolución de la función de estructura con k
para distintos tiempos en β=0.5
3. CONCLUSIONES
El modelo presentado ha permitido describir
cualitativamente el proceso de descomposición en dos
fases, una rica en un elemento A y otra rica en otro
elemento B a partir de una aleación binaria AB en
estado de solución sólida.
Se observa el crecimiento de las fases segregadas en el
máximo de la evolución de la función de estructura, a
lo largo del tiempo de simulación, hacia valores de k
cada vez menores.
Para poder realizar una adecuada cuantificación de la
cinética de crecimiento se requieren simulaciones
montecarlo en mallas de mayor número de espines, a
fin de reducir la dispersión observada.
[1] M. Doi, Progess Material Science, 40, 1966,
pp.79-180.
[2] J. Cahn and J. Hilliard, Journal Chemical Physics
28, 2, 1958, pp. 258-267.
[3] J. Cahn and J. Hilliard, Journal Chemical Physics
31, 3, 1959, pp. 688-699.
[4] J. Cahn, Acta Metallurgica., 9, 1961, pp. 795-801.
[5] J. Cahn and J. Hilliard, Acta Metallurgica, 19,
1971, pp. 151-161.
[6] S.M. Allen and J. Cahn, Acta Metallurgica 27,
1979, pp. 1084-1095.
[7] Danan Fan, Long-Quing Chen, S.P. Chen, Peter
W. Voorhees, Comutational Material Science 9, 1998,
pp. 329-336.
[8] Danan Fan, Long-Quing Chen, S.P. Chen, Peter
W. Voorhees, Acta Materialia, 50, 2002, pp. 18951907.
[9] T.M. Rogers, K.R. Elder and Rashmi C. Desai,
Physics Review B 37, 16,1998, pp. 9638-9649.
[10] E.M. Lifshitz y L.P. Pitaevskii, Física
Estadística, Parte II,Curso de Física Teórica vol 9,
Reverté, pp. 208 (1986).
[11] A.B. Bortz, M.H. Kalos, J.L. Lebowitz and M.A.
Zendejas, Physics Review B 10, 2, 1974, pp. 535-541.
[12] J. Marro, A.B. Bortz, M.H. Kalos and J.L.
Lebowitz, Physics Review B 12, 6, 1975, pp. 20002011.
[13] J.L. Lebowitz, J. Marro and M.H. Kalos, Acta
Metallurgica, 30, 1982, pp. 297-310.
[14] A. Chakrabarti, R. Toral, J.D. Gunton, Physics
Review B 39, 7, 1989, pp. 4386-4394 .
[15] A. Chakrabarti, R. Toral, J.D. Gunton, Physics
Review E 47, 5, 1993, pp.3025-3038.