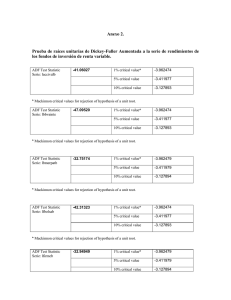
Contraste de Cointegración entre consumo e PIB en Grecia

CONTRASTE DE COINTEGRACIÃ N ENTRE CONSUMO E PIB EN GRECIA
A análise da cointegración e os modelos con correción de erro é unha das metodoloxÃ−as utilizadas
para ó análise da causalidade entre variables económicas.
As regresións espurias (Granger e Newbold,1974) son as que existen entre 2 variables que mostran as
seguintes caracterÃ−sticas : a)non mantenhen entre s iunha relación causal b)a estimación dun modelo
econométrico temporal, que relaciona a unha delas coa outra, proporciona elevada bondade do axuste e un
valor do estatÃ−stico Durbin-Watson (dw) baixo, inferior o valor 2 que corresponderÃ−a á ausencia de
autocorrelación e inferior o lÃ−mite inferior do test de Durbin-Watson.
Realizo a análise de cointegración entre o consumo privado de Grecia (C90GR) e o Producto interior bruto
(PIB90GR) no perÃ−odo 1960-1995 , expresado en miles de millóns de dólaresde 1990 . Considerando as
opcións do test ADF : (N ,1) ,(C,1) e (T,1).
Tomo como referencia bibliográfica o documento nº61 da serie Economic Development. (
http//:www.usc.es/economet )
DATOS TABLA
1961
1962
1963
1964
1965
1966
1967
1968
1969
1970
1971
1972
1973
1974
1975
1976
1977
1978
1979
1980
1981
1982
1983
1984
1985
16.98000
17.70000
18.60000
20.23000
21.78000
23.25000
24.70000
26.40000
28.03000
30.50000
32.19000
34.44000
37.07000
37.32000
39.36000
41.45000
43.34000
45.81000
47.01000
47.09000
48.05000
49.92000
50.05000
50.90001
52.89000
23.80000
24.16000
26.61000
28.81000
31.51000
33.43000
35.27000
37.62000
41.34000
44.63000
47.81000
52.05000
55.86000
53.83000
57.09000
60.72000
62.80000
67.01000
69.48000
70.70000
70.74000
71.02000
71.30000
73.26000
75.55000
1
1986
1987
1988
1989
1990
1991
1992
1993
1994
1995
53.24000
53.89000
55.81000
59.21000
60.74000
62.46000
63.95000
63.45000
64.74000
66.53000
76.78000
76.42000
79.82000
82.89000
82.91000
85.47000
86.08000
84.67000
86.40000
88.21000
Primeiro: Analizamos a evolución conxunta da series C90GR e PIB90GR :
Modelo 1: Relación a longo prazo
Plantexamos a relación a longo prazo entre as variables C90GR e PIB90GR mediante a estimación do
seguinte modelo estático:
LS C90GR C PIB90GR
Dependent Variable: C90GR
Method: Least Squares
Date: 05/04/07 Time: 12:03
Sample: 1960 1995
Included observations: 36
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
C
PIB90GR
-1.758171
0.733709
0.827793
0.013133
-2.123926
55.86705
0.0410
0.0000
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.989224
0.988907
1.667172
94.50177
-68.45358
0.210306
    Mean dependent var
    S.D. dependent var
    Akaike info criterion
    Schwarz criterion
    F-statistic
    Prob(F-statistic)
41.80500
15.82905
3.914088
4.002061
3121.127
0.000000
A análise dos resultados da regresión manifesta unha elevada bondade do axuste
R2 =0,98 .Os signos son os esperados, as variables explicativas teñen un efeito estadÃ−sticamente
significativo, pero o Durbin-Watson é baixo: 0,21. Con estos resultados temos que estudar se se trata dunha
regresión espuria.
Introducimos no comando do computador : GENR ERROR1=RESID
Test de raÃ−ces unitarias: é a metodologÃ−a utilizada para contrastar a estacionariedade da perturbación
mediante un test no que a hipótese que se contrasta é o valor unitariodun determinado coeficiente
autorregresivo (a1) mediante ó análise da nulidade de (a1-1). Baixo determinadas hipóteses se o modelo
2
esta bem especificado a pert5urbación será estacionaria e o coeficiente a1 será menor que 1.Si se rechaza
a hipótese de que (a1-1) é igual a cero e hai9 evidencias de que (a1-1) menor a cero, enton aceitase que a
perturbación é estacionaria e que a regresión é nonespuria.Si se aceita a hipótese (a1-1)=0 e hai
evidencia de que (a1-1) é maior o igual a cero a perturbación non é estacionaria e , según os
defensores deste enfoque, a regresión considerase espuria ou non causal. Problemas deste enfoque: a
identidade que se fai nel é entre non estacionariedade da perturbación e a regresión espuria , mas existen
regresiones non espurias con perturbacións non estacionarias e regresións espurias con perturbacións non
estacionarias.
Aplicamos o test de raÃ−z unitaria ADF á serie de residuos ERROR1, para a súa análise de
estacionariedade.
Na proba de Dickey-Fuller aumentado partese da ecuación:
D(ERROR)= ï“¢o+ï“¢1*t+δïδªERROR(-1)+ ï“¡iï“ D(ERROR(-i))+ ï“¥t
A proba de Dickey-Fuller (un dos test da raÃ−z unitaria) aplicase a regresións do tipo:
D(ERROR)= δïδªERROR(-1)+ ï“−t N=sen ordeada na origen.
UROOT(N,1) ERROR1
Null Hypothesis: ERROR1 has a unit root
Exogenous: None
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-0.663037
-2.634731
-1.951000
-1.610907
 0.4224
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR1)
Method: Least Squares
Date: 05/04/07 Time: 12:07
ï“´= -0.663037 . Aceitamos a Ho do 1%,5% e 10%. Aceitamos a hipótese nula de “non
cointegración”cando o valor estatÃ−stico de proba ï“´ este á dereita dos nÃ−veis crÃ−ticos na cola
esquerda da distribución.A aceptación con frecuencia non indica ausencia de cointegración e pode deberse
a : i) a existencia dunha clara evidencia empÃ−rica favorable a dita hipótese ii)a existencia dunha gran
incertidume , posta de manifesto por unha gran amplitude do intervalo de confianza do parámetro.
Ecuación do test con C=con ordenada na origen:
D(ERROR)= ï“¢o+δïδªERROR(-1)+ ï“−t
UROOT(C,1) ERROR1
Null Hypothesis: ERROR1 has a unit root
3
Exogenous: Constant
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-3.850125
-3.653730
-2.957110
-2.617434
 0.0061
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR1)
Method: Least Squares
Date: 05/04/07 Time: 12:10
ï“´= -3.850125. Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non
cointegración”cando o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola
esquerda da distribución. Isto indica que os residuos da regresión son estacionarios , polo q as variables
estan cointegradas e a regresión serÃ−a non espuria.
Ecuación do test con T= con ordeada na origen e tendencia t.
D(ERROR)= ï“¢o+ï“¢1*t+δïδªERROR(-1)+ ï“−t
UROOT(T,1) ERROR1
Null Hypothesis: ERROR1 has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.756543
-4.296729
-3.568379
-3.218382
 0.0033
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR1)
Method: Least Squares
ï“´= -4.756543. Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non
cointegración”cando o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola
esquerda da distribución. Isto indica que os residuos da regresión son estacionarios , polo q as variables
estan cointegradas e a regresión serÃ−a non espuria.
Modelo 2: Modelo en primeiras diferencias
LS D(C90GR) C D(PIB90GR)
4
Dependent Variable: D(C90GR)
Method: Least Squares
Date: 05/04/07 Time: 12:30
Sample (adjusted): 1961 1995
Included observations: 35 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
C
D(PIB90GR)
0.705920
0.388066
0.150246
0.061564
4.698422
6.303429
0.0000
0.0000
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
0.546287
0.532538
0.553958
10.12668
-27.95979
    Mean dependent var
    S.D. dependent var
    Akaike info criterion
    Schwarz criterion
    Durbin-Watson stat
1.446571
0.810221
1.711988
1.800865
1.932662
A análise dos resultados da regresión manifesta unha bondade do axuste
R2 =0,54 .Os signos son os esperados, as variables explicativas teñen un efeito estadÃ−sticamente
significativo, o Durbin-Watson é : 1,93. Este valor é próximo a 2 que corresponde coa ausencia de
autocorrelación e inferior ó limite do test de Durbin-Watson.
Realizamos á análise da estacionariedade dos residuos:
GENR ERROR2=RESID
Aplicamos o test da raÃ−z unitaria á serie de residuos ERROR2 par a análise da súa estacionariedade:
D(ERROR)= δïδªERROR(-1)+ ï“−t N=sen ordeada na origen.
UROOT(N,1) ERROR2
Null Hypothesis: ERROR2 has a unit root
Exogenous: None
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.486144
-2.636901
-1.951332
-1.610747
 0.0001
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR2)
Method: Least Squares
Date: 05/04/07 Time: 12:31
Sample (adjusted): 1963 1995
5
Included observations: 33 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
ERROR2(-1)
D(ERROR2(-1))
-1.120630
0.127281
0.249798
0.176625
-4.486144
0.720630
0.0001
0.4765
R-squared
0.502447
    Mean dependent var
0.015373
Adjusted R-squared
0.486397
    S.D. dependent var
0.778232
S.E. of regression
0.557729
    Akaike info criterion 1.728803
Sum squared resid
9.642895
    Schwarz criterion
1.819500
Log likelihood
-26.52525
    Durbin-Watson stat
1.935393
ï“´= -4.486144 . Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non
cointegración”cando o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola
esquerda da distribución. Isto indica que os residuos da regresión son estacionarios , polo q as variables
estan cointegradas e a regresión serÃ−a non espuria.
Ecuación do test con C=con ordenada na origen:
D(ERROR)= ï“¢o+δïδªERROR(-1)+ ï“−t
UROOT(C,1) ERROR2
Null Hypothesis: ERROR2 has a unit root
Exogenous: Constant
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.415111
-3.646342
-2.954021
-2.615817
 0.0014
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR2)
Method: Least Squares
Date: 05/04/07 Time: 12:32
Sample (adjusted): 1963 1995
Included observations: 33 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
ERROR2(-1)
D(ERROR2(-1))
C
-1.120405
0.126703
0.019413
0.253766
0.179453
0.098647
-4.415111
0.706051
0.196795
0.0001
0.4856
0.8453
R-squared
Adjusted R-squared
0.503089
0.469961
    Mean dependent var
    S.D. dependent var
0.015373
0.778232
6
S.E. of regression
0.566582
    Akaike info criterion 1.788119
Sum squared resid
9.630463
    Schwarz criterion
1.924165
Log likelihood
-26.50396
    F-statistic
15.18648
Durbin-Watson stat
1.937281
    Prob(F-statistic)
0.000028
ï“´= -4.415111 . Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non
cointegración”cando o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola
esquerda da distribución. Isto indica que os residuos da regresión son estacionarios , polo q as variables
estan cointegradas e a regresión serÃ−a non espuria.
Ecuación do test con T= con ordeada na origen e tendencia t.
D(ERROR)= ï“¢o+ï“¢1*t+δïδªERROR(-1)+ ï“−t
UROOT(T,1) ERROR2
Null Hypothesis: ERROR2 has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.596575
-4.262735
-3.552973
-3.209642
 0.0044
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR2)
Method: Least Squares
ï“´=-4.596575. Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non
cointegración”cando o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola
esquerda da distribución. . Isto indica que os residuos da regresión son estacionarios , polo q as variables
estan cointegradas e a regresión serÃ−a non espuria.
Modelo 3. Modelo Dinámico Mixto: Combinamos niveÃ−s e incrementos , tendo en conta a endógena
retardada como variable esplicativa.
LS C90GR C D(PIB90GR) C90GR(-1)
Dependent Variable: C90GR
Method: Least Squares
Date: 05/04/07 Time: 12:37
Sample (adjusted): 1961 1995
Included observations: 35 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
C
D(PIB90GR)
0.323981
0.414050
0.338029
0.064424
0.958441
6.426984
0.3450
0.0000
7
C90GR(-1)
1.008087
0.006425
156.9054
0.0000
R-squared
0.998806
    Mean dependent var
42.54514
Adjusted R-squared
0.998731
    S.D. dependent var
15.41516
S.E. of regression
0.549118
    Akaike info criterion 1.720811
Sum squared resid
9.648989
    Schwarz criterion
1.854126
Log likelihood
-27.11419
    F-statistic
13381.17
Durbin-Watson stat
2.064245
    Prob(F-statistic)
0.000000
A análise dos resultados da regresión manifesta unha bondade do axuste moi boa
R2 =0,99 .Os signos son os esperados, as variables explicativas teñen un efeito estadÃ−sticamente
significativo, o Durbin-Watson é : 2,06. Este valor é maior a 2 que corresponde coa ausencia de
autocorrelación e inferior ó limite do test de Durbin-Watson.
GENR ERROR1=RESID
Aplicamos o test da raÃ−z unitaria ADF á serie de residuos ERROR3 para a súa análise de
estacionariedade.
D(ERROR)= δïδªERROR(-1)+ ï“−t N=sen ordeada na origen.
UROOT(N,1) ERROR3
Null Hypothesis: ERROR3 has a unit root
Exogenous: None
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.790025
-2.636901
-1.951332
-1.610747
 0.0000
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR3)
Method: Least Squares
ï“´=-4.790025 . Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non
cointegración”cando o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola
esquerda da distribución. . Isto indica que os residuos da regresión son estacionarios , polo q as variables
estan cointegradas e a regresión serÃ−a non espuria.
Ecuación do test con C=con ordenada na origen:
D(ERROR)= ï“¢o+δïδªERROR(-1)+ ï“−t
UROOT (C,1) ERROR3
Null Hypothesis: ERROR3 has a unit root
8
Exogenous: Constant
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.713318
-3.646342
-2.954021
-2.615817
 0.0006
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR3)
ï“´=-4.71 . Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non cointegración”cando
o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola esquerda da distribución.
Isto indica que os residuos da regresión son estacionarios , polo q as variables estan cointegradas e a
regresión serÃ−a non espuria.
Ecuación do test con T= con ordeada na origen e tendencia t.
D(ERROR)= ï“¢o+ï“¢1*t+δïδªERROR(-1)+ ï“−t
UROOT(T,1) ERROR3
Null Hypothesis: ERROR3 has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.634208
-4.262735
-3.552973
-3.209642
 0.0040
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR3)
ï“´=-463 . Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non cointegración”cando o
valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola esquerda da distribución.
Isto indica que os residuos da regresión son estacionarios , polo q as variables estan cointegradas e a
regresión serÃ−a non espuria.
Modelo 4. Modelo correción de error con Dx
Seguindo o proceso bietápico de Engel e Granger (1987) .Primeiro estimase a relación entra as variables a
longo prazo , e despoÃ−s estimanse as ecuacións pero coas variables en diferencias e incluÃ−ndo os
residuos retardados obtidos nas regresións da primeira etapa.
Relación a corto plazo. Tomanse as variables en primeiras diferencias e incorporamos os residuos do modelo
9
da relación a longo prazo retardados un perÃ−odo (ERROR1(-1)) como variable esplicativa.
LS D(C90GR) C D(PIB90GR) ERROR1(-1)
Dependent Variable: D(C90GR)
Method: Least Squares
Date: 05/04/07 Time: 12:43
Sample (adjusted): 1965 1995
Included observations: 31 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
C
PIB90GR
ERROR1(-1)
1.860778
-0.005723
-0.223401
0.611201
0.009105
0.208156
3.044461
-0.628496
-1.073241
0.0050
0.5348
0.2923
R-squared
0.068667
    Mean dependent var
1.493548
Adjusted R-squared
0.002144
    S.D. dependent var
0.841754
S.E. of regression
0.840851
    Akaike info criterion 2.582962
Sum squared resid
19.79686
    Schwarz criterion
2.721734
Log likelihood
-37.03590
    F-statistic
1.032224
Durbin-Watson stat
1.811362
    Prob(F-statistic)
0.369375
A análise dos resultados da regresión manifesta unha bondade do axuste moi mala
R2 =0,068 .Os signos son os esperados, as variables explicativas teñen un efeito estadÃ−sticamente
significativo, o Durbin-Watson é : 1,81. Este valor é próximo a 2 que corresponde coa ausencia de
autocorrelación e inferior ó limite do test de Durbin-Watson.
D(ERROR)= δïδªERROR(-1)+ ï“−t N=sen ordeada na origen.
UROOT(N,1) ERROR4
Null Hypothesis: ERROR4 has a unit root
Exogenous: None
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.409941
-2.647120
-1.952910
-1.610011
 0.0001
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR4)
Method: Least Squares
Date: 05/04/07 Time: 12:44
Sample (adjusted): 1967 1995
10
Included observations: 29 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
ERROR4(-1)
D(ERROR4(-1))
-1.119320
0.227417
0.253817
0.187979
-4.409941
1.209803
0.0001
0.2368
R-squared
0.482260
    Mean dependent var
0.026495
Adjusted R-squared
0.463085
    S.D. dependent var
1.130744
S.E. of regression
0.828547
    Akaike info criterion 2.528185
Sum squared resid
18.53522
    Schwarz criterion
2.622481
Log likelihood
-34.65868
    Durbin-Watson stat
1.934562
ï“´=-4,40 . Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non cointegración”cando
o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola esquerda da distribución.
Isto indica que os residuos da regresión son estacionarios , polo q as variables estan cointegradas e a
regresión serÃ−a non espuria.
Ecuación do test con C=con ordenada na origen:
D(ERROR)= ï“¢o+δïδªERROR(-1)+ ï“−t
UROOT(C,1) ERROR4
Null Hypothesis: ERROR4 has a unit root
Exogenous: Constant
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.324869
-3.679322
-2.967767
-2.622989
 0.0020
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR4)
Method: Least Squares
Date: 05/04/07 Time: 12:46
Sample (adjusted): 1967 1995
Included observations: 29 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
ERROR4(-1)
D(ERROR4(-1))
C
-1.118850
0.227133
0.011701
0.258702
0.191577
0.156820
-4.324869
1.185598
0.074611
0.0002
0.2465
0.9411
R-squared
Adjusted R-squared
0.482371
0.442554
    Mean dependent var
    S.D. dependent var
0.026495
1.130744
11
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.844240
18.53125
-34.65558
1.935430
    Akaike info criterion
    Schwarz criterion
    F-statistic
    Prob(F-statistic)
2.596936
2.738381
12.11453
0.000192
ï“´=-4,32 . Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non cointegración”cando
o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola esquerda da distribución. .
Isto indica que os residuos da regresión son estacionarios , polo q as variables estan cointegradas e a
regresión serÃ−a non espuria.
Ecuación do test con T= con ordeada na origen e tendencia t.
D(ERROR)= ï“¢o+ï“¢1*t+δïδªERROR(-1)+ ï“−t
UROOT(T,1) ERROR4
Null Hypothesis: ERROR4 has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.263654
-4.309824
-3.574244
-3.221728
 0.0111
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR4)
Method: Least Squares
Date: 05/04/07 Time: 12:48
Sample (adjusted): 1967 1995
Included observations: 29 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
ERROR4(-1)
D(ERROR4(-1))
C
@TREND(1960)
-1.127038
0.231123
0.147487
-0.006472
0.264336
0.195283
0.432238
0.019146
-4.263654
1.183529
0.341218
-0.338023
0.0003
0.2477
0.7358
0.7382
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.484726
0.422893
0.858998
18.44694
-34.58946
1.934966
    Mean dependent var
    S.D. dependent var
    Akaike info criterion
    Schwarz criterion
    F-statistic
    Prob(F-statistic)
0.026495
1.130744
2.661342
2.849934
7.839302
0.000747
12
ï“´=-4,26 . Rechazamos a Ho do 5% e 10%. Rechazamos a hipótese nula de “non cointegración”cando o
valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola esquerda da distribución.
Aceitamos a Ho do 1%. A aceptación con frecuencia non indica ausencia de cointegración e pode deberse a
: i) a existencia dunha clara evidencia empÃ−rica favorable a dita hipótese ii)a existencia dunha gran
incertidume , posta de manifesto por unha gran amplitude do intervalo de confianza do parámetro.
Modelo 5. Modelo Correción de erro.Relación a c/p sin Dx.
Outra opción para a segunda etapa dun modelo CE , consisten expresar o incremento da variable endógena
en función dos incrementos retardados das variables explicativas e incluÃ−ndo os residuos retardados
obtidos na regresión da relación a longo prazo.
LS D(C90GR) C D(PIB90GR(-1)) ERROR1(-1)
Dependent Variable: D(C90GR)
Method: Least Squares
Date: 05/04/07 Time: 12:49
Sample (adjusted): 1965 1995
Included observations: 31 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
C
D(PIB90GR(-1))
ERROR1(-1)
1.370932
0.061889
-0.168656
0.293734
0.132391
0.278641
4.667251
0.467473
-0.605280
0.0001
0.6438
0.5499
R-squared
0.062843
    Mean dependent var
1.493548
Adjusted R-squared
-0.004097
    S.D. dependent var
0.841754
S.E. of regression
0.843476
    Akaike info criterion 2.589196
Sum squared resid
19.92067
    Schwarz criterion
2.727969
Log likelihood
-37.13254
    F-statistic
0.938798
Durbin-Watson stat
1.908146
    Prob(F-statistic)
0.403063
A análise dos resultados da regresión manifesta unha bondade do axuste moi mala
R2 =0,062 .Os signos son os esperados, as variables explicativas teñen un efeito estadÃ−sticamente
significativo, o Durbin-Watson é : 1,81. Este valor é próximo a 2 que corresponde coa ausencia de
autocorrelación e inferior ó limite do test de Durbin-Watson.
GENR ERROR5=RESID
Aplicamos o test da raÃ−z unitaria á serie de residuos ERROR5 para a súa análise de estacionariedade.
D(ERROR)= δïδªERROR(-1)+ ï“−t N=sen ordeada na origen.
UROOT(N,1)
Null Hypothesis: ERROR5 has a unit root
Exogenous: None
Lag Length: 1 (Fixed)
t-Statistic
  Prob.*
13
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
-4.449977
-2.647120
-1.952910
-1.610011
 0.0001
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR5)
Method: Least Squares
Date: 05/04/07 Time: 12:51
Sample (adjusted): 1967 1995
Included observations: 29 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
ERROR5(-1)
D(ERROR5(-1))
-1.160955
0.213603
0.260890
0.188462
-4.449977
1.133398
0.0001
0.2670
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
0.500655
0.482161
0.837886
18.95544
-34.98374
    Mean dependent var
    S.D. dependent var
    Akaike info criterion
    Schwarz criterion
    Durbin-Watson stat
0.016615
1.164360
2.550603
2.644899
1.927098
ï“´=-4,44 . Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non cointegración”cando
o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola esquerda da distribución. .
Isto indica que os residuos da regresión son estacionarios , polo q as variables estan cointegradas e a
regresión serÃ−a non espuria.
Ecuación do test con C=con ordenada na origen:
D(ERROR)= ï“¢o+δïδªERROR(-1)+ ï“−t
UROOT(C,1) ERROR5
Null Hypothesis: ERROR5 has a unit root
Exogenous: Constant
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.365469
-3.679322
-2.967767
-2.622989
 0.0018
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR5)
14
Method: Least Squares
Date: 05/04/07 Time: 12:51
Sample (adjusted): 1967 1995
Included observations: 29 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
ERROR5(-1)
D(ERROR5(-1))
C
-1.160929
0.213589
0.000649
0.265935
0.192081
0.158600
-4.365469
1.111976
0.004092
0.0002
0.2763
0.9968
R-squared
0.500655
    Mean dependent var
0.016615
Adjusted R-squared
0.462244
    S.D. dependent var
1.164360
S.E. of regression
0.853847
    Akaike info criterion 2.619568
Sum squared resid
18.95542
    Schwarz criterion
2.761012
Log likelihood
-34.98374
    F-statistic
13.03411
Durbin-Watson stat
1.927128
    Prob(F-statistic)
0.000120
ï“´=-4,36 . Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non cointegración”cando
o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola esquerda da distribución. .
. Isto indica que os residuos da regresión son estacionarios , polo q as variables estan cointegradas e a
regresión serÃ−a non espuria.
Ecuación do test con T= con ordeada na origen e tendencia t.
D(ERROR)= ï“¢o+ï“¢1*t+δïδªERROR(-1)+ ï“−t
UROOT(T,1) ERROR5
Null Hypothesis: ERROR5 has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 1 (Fixed)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
  Prob.*
-4.419961
-4.309824
-3.574244
-3.221728
 0.0077
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(ERROR5)
Method: Least Squares
Date: 05/04/07 Time: 12:52
Sample (adjusted): 1967 1995
Included observations: 29 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob. Â
ERROR5(-1)
-1.209555
0.273657
-4.419961
0.0002
15
D(ERROR5(-1))
C
@TREND(1960)
0.239043
0.343778
-0.016372
0.195546
0.438748
0.019502
1.222441
0.783544
-0.839509
0.2329
0.4407
0.4091
R-squared
0.514346
    Mean dependent var
0.016615
Adjusted R-squared
0.456068
    S.D. dependent var
1.164360
S.E. of regression
0.858736
    Akaike info criterion 2.660732
Sum squared resid
18.43570
    Schwarz criterion
2.849325
Log likelihood
-34.58062
    F-statistic
8.825668
Durbin-Watson stat
1.926331
    Prob(F-statistic)
0.000365
ï“´=-4,41 . Rechazamos a Ho do 1%,5% e 10%. Rechazamos a hipótese nula de “non cointegración”cando
o valor estatÃ−stico de proba ï“´ este á esquerda dos nÃ−veis crÃ−ticos na cola esquerda da distribución.
Isto indica que os residuos da regresión son estacionarios , polo q as variables estan cointegradas e a
regresión serÃ−a non espuria.
Olalha Pinheiro Pena
Grupo k-Q
CONTRASTE
DE
COINTEGRACIÃ N
ENTRE
CONSUMO
E
PIB
DE
GRECIA
16