Problemas Resueltos Dis. Experim_1

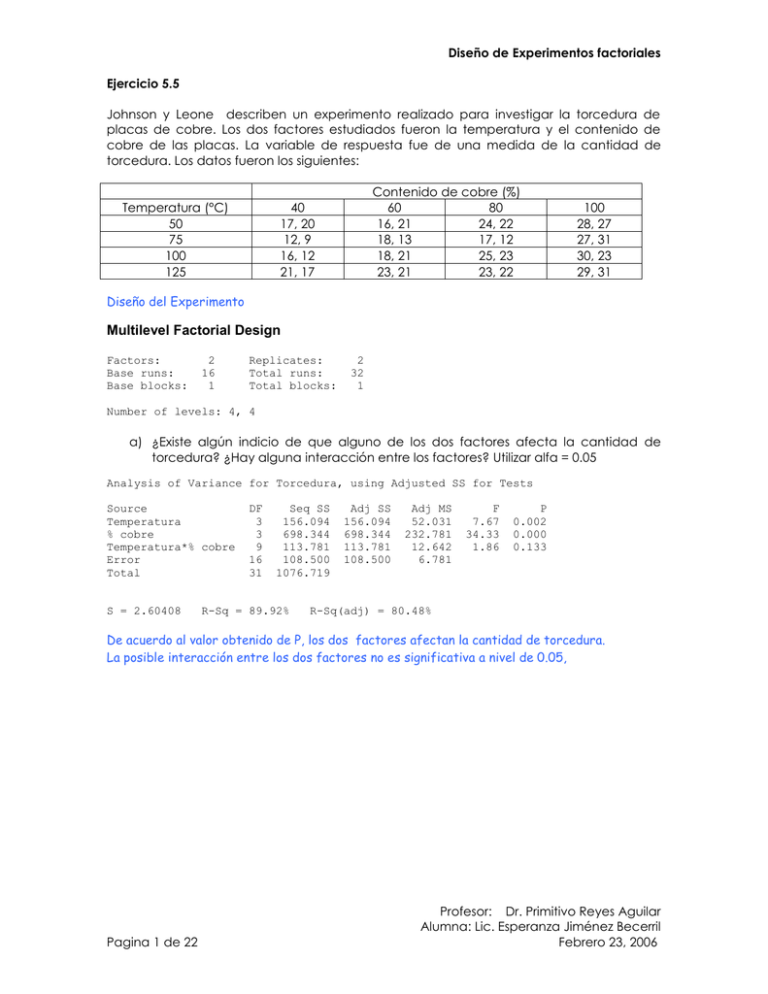
Diseño de Experimentos factoriales
Ejercicio 5.5
Johnson y Leone describen un experimento realizado para investigar la torcedura de
placas de cobre. Los dos factores estudiados fueron la temperatura y el contenido de
cobre de las placas. La variable de respuesta fue de una medida de la cantidad de
torcedura. Los datos fueron los siguientes:
Temperatura (°C)
50
75
100
125
Contenido de cobre (%)
60
80
16, 21
24, 22
18, 13
17, 12
18, 21
25, 23
23, 21
23, 22
40
17, 20
12, 9
16, 12
21, 17
100
28, 27
27, 31
30, 23
29, 31
Diseño del Experimento
Multilevel Factorial Design
Factors:
Base runs:
Base blocks:
2
16
1
Replicates:
Total runs:
Total blocks:
2
32
1
Number of levels: 4, 4
a) ¿Existe algún indicio de que alguno de los dos factores afecta la cantidad de
torcedura? ¿Hay alguna interacción entre los factores? Utilizar alfa = 0.05
Analysis of Variance for Torcedura, using Adjusted SS for Tests
Source
Temperatura
% cobre
Temperatura*% cobre
Error
Total
S = 2.60408
DF
3
3
9
16
31
Seq SS
156.094
698.344
113.781
108.500
1076.719
R-Sq = 89.92%
Adj SS
156.094
698.344
113.781
108.500
Adj MS
52.031
232.781
12.642
6.781
F
7.67
34.33
1.86
P
0.002
0.000
0.133
R-Sq(adj) = 80.48%
De acuerdo al valor obtenido de P, los dos factores afectan la cantidad de torcedura.
La posible interacción entre los dos factores no es significativa a nivel de 0.05,
Pagina 1 de 22
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23, 2006
Diseño de Experimentos factoriales
b) Analizar los residuales de este experimento
Normal Probability Plot of the Residuals
(response is Torcedura)
99
95
90
Percent
80
70
60
50
40
30
20
10
5
1
-3
-2
-1
0
1
Standardized Residual
2
3
La gráfica nos demuestra una normalidad al aproximarse los residuales a la línea recta,
concluyendo que el modelo es válido.
Residuals Versus the Fitted Values
(response is Torcedura)
Standardized Residual
2
1
0
-1
-2
10
15
20
Fitted Value
25
30
Los residuales son aleatorios por arriba y por debajo de la línea, concluyéndose que existe
independencia en la respuesta.
Pagina 2 de 22
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23, 2006
Diseño de Experimentos factoriales
c) Graficar la torcedura promedio con cada nivel del contenido de cobre y
compararlas con una distribución t con la escala apropiada. Describir las
diferencias en los efectos de los diversos niveles del contenido de cobre sobre la
torcedura. Si es deseable una torcedura baja, ¿qué nivel del contenido de cobre
debería de especificarse?
Main Effects Plot (data means) for Torcedura
Temperatura
30.0
% cobre
Mean of Torcedura
27.5
25.0
22.5
20.0
17.5
15.0
50
75
100
125
40
60
80
100
Esta gráfica nos muestra que a mayor contenido de cobre es mayor el nivel de torcedura,
siendo este incremento mayor a partir de 80% de cobre.
Si lo que buscamos es una menor torcedura se recomendaría el 40% de cobre.
Interaction Plot (data means) for Torcedura
Temperatura
50
75
100
125
30
Mean
25
20
15
10
40
60
80
100
% cobre
Pagina 3 de 22
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23, 2006
Diseño de Experimentos factoriales
d) Suponga que no es sencillo controlar la temperatura en el medio ambiente donde
van a usarse las placas de cobre ¿Este hecho modifica la respuesta que se dio en
el inciso c?
No, ya que la interacción cobre temperatura es no significativa
Ejercicio 5.16
El porcentaje de la concentración de madera dura en la pulpa bruta, la presión de la
cuba y el tiempo de cocción de la pulpa se investiga en cuanto a sus efectos sobre la
resistencia del papel. Se seleccionan tres niveles de la concentración de madera dura,
tres niveles de la presión y dos tiempos de cocción. Se lleva a cabo un experimento
factorial con dos réplicas, obteniéndose los siguientes datos:
% de la
concentración
de la madera
2
4
8
Tiempo de cocción 3.0
Presión
400
500
650
196.6
197.7
199.8
196.0
196.0
199.4
198.5
196.0
198.4
197.2
196.9
197.6
197.5
195.6
197.4
196.6
196.2
198.1
Tiempo de cocción 4.0
Presión
400
500
650
198.4
199.6
200.6
198.6
200.4
200.9
197.5
198.7
199.6
198.1
198.0
199.0
197.6
197.0
198.5
198.4
197.8
199.8
Diseño del Modelo
Multilevel Factorial Design
Factors:
Base runs:
Base blocks:
3
18
1
Replicates:
Total runs:
Total blocks:
2
36
1
Number of levels: 3, 3, 2
a) Analizar los datos y sacar conclusiones. Utilizar alfa = 0.05
General Linear Model: Resistencia versus % concentrac, Presión, Tiempo
Factor
% concentración
Presión
Tiempo
Pagina 4 de 22
Type
fixed
fixed
fixed
Levels
3
3
2
Values
2, 4, 8
400, 500, 650
3, 4
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23, 2006
Diseño de Experimentos factoriales
Analysis of Variance for Resistencia, using Adjusted SS for Tests
Source
% concentración
Presión
Tiempo
% concentración*Presión
% concentración*Tiempo
Presión*Tiempo
% concentración*Presión*Tiempo
Error
Total
S = 0.715503
R-Sq = 87.08%
DF
2
2
1
4
2
2
4
18
35
Seq SS
7.5939
17.6172
22.8803
6.4311
1.4772
3.5172
2.5778
9.2150
71.3097
Adj SS
7.5939
17.6172
22.8803
6.4311
1.4772
3.5172
2.5778
9.2150
Adj MS
3.7969
8.8086
22.8803
1.6078
0.7386
1.7586
0.6444
0.5119
F
7.42
17.21
44.69
3.14
1.44
3.44
1.26
P
0.004
0.000
0.000
0.040
0.262
0.054
0.322
R-Sq(adj) = 74.87%
El análisis de varianza nos muestra que los factores porcentaje de concentración, presión y
tiempo son significativos así como la interacción concentración-presión.
b) Construir las gráficas de los residuales apropiadas y comentar la adecuación del
modelo
Normal Probability Plot of the Residuals
(response is Resistencia)
99
95
90
Percent
80
70
60
50
40
30
20
10
5
1
-3
Pagina 5 de 22
-2
-1
0
1
Standardized Residual
2
3
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23, 2006
Diseño de Experimentos factoriales
Residuals Versus the Fitted Values
(response is Resistencia)
3
Standardized Residual
2
1
0
-1
-2
-3
196
197
198
199
Fitted Value
200
201
Las gráficas nos muestras que existe normalidad por lo que es válido el modelo y hay
independencia de los factores con los resultados
c) ¿Bajo qué conjunto de condiciones debería operarse este proceso? ¿Por qué?
Éste modelo para maximizar la resistencia nos sugiere que se aplique el porcentaje de
concentración 2 y la presión de 650, así como el tiempo de cocción de 4 horas. (basado en las
siguientes gráficas)
Main Effects Plot (data means) for Resistencia
% concentración
Presión
199.0
Mean of Resistencia
198.5
198.0
197.5
2
4
Tiempo
8
400
500
650
199.0
198.5
198.0
197.5
3
Pagina 6 de 22
4
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23, 2006
Diseño de Experimentos factoriales
Interaction Plot (data means) for Resistencia
400
500
650
3
4
200
198
% concentr ación
196
200
198
P r esión
% concentración
2
4
8
Presión
400
500
650
196
T iempo
Ejercicio 5.17
El departamento de control de calidad de una planta de acabados textiles estudia el
efecto de varios factores sobre el teñido de una tela de algodón y fibras sintéticas
utilizadas para fabricar camisas para caballero. Se seleccionaron tres operadores, tres
duraciones del ciclo y dos temperaturas, y se tiñeron tres ejemplares pequeños de la tela
bajo cada conjunto de condiciones. La tela terminada se comparó con un patrón, y se le
asignó una evaluación numérica. Los datos se presentan enseguida. Analizar los datos y
sacar conclusiones. Comentar la adecuación del modelo.
Temperatura
Duración
del ciclo
40
50
60
Pagina 7 de 22
1
23
24
25
36
35
36
28
24
27
300°
Operador
2
27
28
26
34
38
39
35
35
34
3
31
32
29
33
34
35
26
27
25
1
24
23
28
37
39
35
26
29
25
350°
Operador
2
39
36
35
34
38
36
36
37
34
3
34
36
39
34
36
31
28
26
24
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23, 2006
Diseño de Experimentos factoriales
Diseño del Modelo
Multilevel Factorial Design
Factors:
Base runs:
Base blocks:
3
18
1
Replicates:
Total runs:
Total blocks:
3
54
1
Number of levels: 3, 2, 3
General Linear Model: Teñido versus Duración, Temperatura, Operador
Factor
Duración
Temperatura
Operador
Type
fixed
fixed
fixed
Levels
3
2
3
Values
40, 50, 60
300, 350
1, 2, 3
Analysis of Variance for Teñido, using Adjusted SS for Tests
Source
Duración
Temperatura
Operador
Duración*Temperatura
Duración*Operador
Temperatura*Operador
Duración*Temperatura*Operador
Error
Total
DF
2
1
2
2
4
2
4
36
53
Seq SS
432.704
52.019
267.148
82.259
353.519
12.481
49.074
122.000
1371.204
Adj SS
432.704
52.019
267.148
82.259
353.519
12.481
49.074
122.000
Adj MS
216.352
52.019
133.574
41.130
88.380
6.241
12.269
3.389
F
63.84
15.35
39.42
12.14
26.08
1.84
3.62
P
0.000
0.000
0.000
0.000
0.000
0.173
0.014
El análisis de la varianza muestra que los factores duración, temperatura, operador y las
interrelaciones duración temperatura, duración operador tienen un efecto significativo.
S = 1.84089
R-Sq = 91.10%
R-Sq(adj) = 86.90%
Normal Probability Plot of the Residuals
(response is Teñido)
99
95
90
Percent
80
70
60
50
40
30
20
10
5
1
-3
Pagina 8 de 22
-2
-1
0
1
Standardized Residual
2
3
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23, 2006
Diseño de Experimentos factoriales
La gráfica de normalidad de los residuos nos muestra que están distribuidos cerca de la recta,
lo que nos valida el modelo
Residuals Versus the Fitted Values
(response is Teñido)
Standardized Residual
2
1
0
-1
-2
25.0
27.5
30.0
Fitted Value
32.5
35.0
37.5
La distribución por arriba y por debajo de la línea nos denota independencia
Interaction Plot (data means) for Teñido
300
350
1
2
3
35
30
Dur ación
Duración
40
50
60
25
35
Temperatura
300
350
30
T emper atur a
25
O per ador
El mejor teñido se da con las condiciones de duración del ciclo en 50, con el operador 2 y la
temperatura de 350°.
Ejercicio 5.19
Pagina 9 de 22
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23, 2006
Diseño de Experimentos factoriales
Se estudia el rendimiento de un proceso químico. Los dos factores de interés son la
temperatura y la presión. Se seleccionan tres niveles de cada factor; sin embargo, sólo es
posible hacer nueve corridas en un día. El experimentador corre una réplica en cada día.
Los datos se muestran en la tabla siguiente. Analizar los datos, suponiendo que los días son
bloques.
Temperatura
Baja
Intermedia
Alta
Día 1
Presión
260
84.0
87.3
90.2
250
86.3
88.5
89.1
270
85.8
89.0
91.3
Día 2
Presión
260
85.2
89.9
93.2
250
86.1
89.4
91.7
270
87.3
90.3
93.7
Diseño del Modelo
Multilevel Factorial Design
Factors:
Base runs:
Base blocks:
2
9
1
Replicates:
Total runs:
Total blocks:
2
18
2
Number of levels: 3, 3
General Linear Model: Rendimiento versus Blocks, Temperatura, Presion
Factor
Blocks
Temperatura
Presion
Type
fixed
fixed
fixed
Levels
2
3
3
Values
1, 2
1, 2, 3
250, 260, 270
Analysis of Variance for Rendimiento, using Adjusted SS for Tests
Source
Blocks
Temperatura
Presion
Temperatura*Presion
Error
Total
S = 0.728869
DF
1
2
2
4
8
17
Seq SS
13.005
99.854
5.508
4.452
4.250
127.069
R-Sq = 96.66%
Adj SS
13.005
99.854
5.508
4.452
4.250
Adj MS
13.005
49.927
2.754
1.113
0.531
F
24.48
93.98
5.18
2.10
P
0.001
0.000
0.036
0.173
R-Sq(adj) = 92.89%
El análisis de varianza nos muestra que la temperatura tiene un efecto significativo, que la
presión tiene un efecto muy bajo y que la interacción Temperatura presión no es significativa.
Pagina 10 de 22
2006
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
Normal Probability Plot of the Residuals
(response is Rendimiento)
99
95
90
Percent
80
70
60
50
40
30
20
10
5
1
-3
-2
-1
0
1
Standardized Residual
2
3
Los puntos cerca de la recta nos indican que el modelo es válido
Residuals Versus the Fitted Values
(response is Rendimiento)
Standardized Residual
2
1
0
-1
-2
84
85
86
87
88
89
Fitted Value
90
91
92
93
Los puntos en forma aleatoria arriba y debajo de la recta nos indican independencia de la
respuesta
Pagina 11 de 22
2006
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
Main Effects Plot (data means) for Rendimiento
Temperatura
92
Presion
Mean of Rendimiento
91
90
89
88
87
86
85
1
2
3
250
260
270
La gráfica nos indica que al aumentar la temperatura se aumenta el rendimiento, en lo que
corresponde a la presión baja el rendimiento cuando es de 250 a 260 y aumenta cuando paso de
260 a 270.
Interaction Plot (data means) for Rendimiento
93
Temperatura
1
2
3
92
91
Mean
90
89
88
87
86
85
84
250
260
Presion
270
Como lo que se desea es aumentar el rendimiento se recomendaría la temperatura 3 con
presión de 270.
Ejercicio 6.1
Pagina 12 de 22
2006
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
Un ingeniero está interesado en los efectos de la velocidad de corte (A), la geometría de
la herramienta (B) y el ángulo de corte (C) sobre la vida (en horas) de una máquina
herramienta. Se eligen dos niveles de cada factor y se corren tres réplicas de un diseño
factorial 23. Los resultados fueron los siguientes:
A
B
C
+
+
+
+
+
+
+
+
+
+
+
+
Combinación
tratamientos
(1)
a
b
ab
c
ac
bc
abc
de
Réplicas
I
22
32
35
55
44
40
60
39
II
31
43
34
47
45
37
50
41
III
25
29
50
46
38
36
54
47
Full Factorial Design
Factors:
Runs:
Blocks:
3
24
1
Base Design:
Replicates:
Center pts (total):
3, 8
3
0
All terms are free from aliasing.
a)
estimar los efectos de los factores. ¿Qué efectos parecen ser grandes?
Factorial Fit: Vida versus A, B, C
Estimated Effects and Coefficients for Vida (coded units)
Term
Constant
A
B
C
A*B
A*C
B*C
A*B*C
Effect
0.250
11.250
6.750
-1.750
-8.917
-2.917
-2.250
S = 5.44289
Coef
40.792
0.125
5.625
3.375
-0.875
-4.458
-1.458
-1.125
SE Coef
1.111
1.111
1.111
1.111
1.111
1.111
1.111
1.111
R-Sq = 77.25%
T
36.72
0.11
5.06
3.04
-0.79
-4.01
-1.31
-1.01
P
0.000
0.912
0.000
0.008
0.442
0.001
0.208
0.326
R-Sq(adj) = 67.30%
Los efectos mayores son producidos por los factores B, C y la interacción AC
Pagina 13 de 22
2006
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
Normal Probability Plot of the Standardized Effects
(response is Vida, Alpha = .05)
99
Effect Ty pe
Not Significant
Significant
95
80
Percent
F actor
A
B
C
B
90
C
70
N ame
A
B
C
60
50
40
30
20
10
AC
5
1
-5.0
-2.5
0.0
2.5
Standardized Effect
5.0
La gráfica anterior nos confirma que los factores significativos son A y B así como la
interacción AC
Pareto Chart of the Standardized Effects
(response is Vida, Alpha = .05)
2.120
F actor
A
B
C
B
N ame
A
B
C
AC
Term
C
BC
ABC
AB
A
0
1
2
3
Standardized Effect
4
5
En esta gráfica se aprecia que los efectos en orden ascendente son el factor B, la interacción
AC y el factor C
b)
Usar el análisis de varianza para confirmar las conclusiones del inciso a.
Analysis of Variance for Vida (coded units)
Source
Pagina 14 de 22
2006
DF
Seq SS
Adj SS
Adj MS
F
P
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
Main Effects
2-Way Interactions
3-Way Interactions
Residual Error
Pure Error
Total
Pagina 15 de 22
2006
3
3
1
16
16
23
1033.12
546.46
30.37
474.00
474.00
2083.96
1033.12
546.46
30.37
474.00
474.00
344.37
182.15
30.37
29.63
29.63
11.62
6.15
1.03
0.000
0.006
0.326
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
c)
Escribir un modelo de regresión para predecir la vida de la herramienta (en horas)
con base en los resultados de este experimento.
yˆ  40.7925 5.625A  3.375B  4.458AC
d)
Analizar los residuales. ¿hay algún problema evidente?
De acuerdo a las gráficas siguientes no se presenta evidencia de problema
Normal Probability Plot of the Residuals
(response is Vida)
99
95
90
Percent
80
70
60
50
40
30
20
10
5
1
-3
-2
-1
0
1
Standardized Residual
2
3
Residuals Versus the Fitted Values
(response is Vida)
2.5
Standardized Residual
2.0
1.5
1.0
0.5
0.0
-0.5
-1.0
25
Pagina 16 de 22
2006
30
35
40
Fitted Value
45
50
55
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
e)
Con base en el análisis de las gráficas de los efectos principales y las
interacciones, ¿Cuáles serían los niveles de A, B y C que se recomendaría utilizar?
Main Effects Plot (data means) for Vida
A
B
45.0
42.5
Mean of Vida
40.0
37.5
35.0
-1
1
-1
1
C
45.0
42.5
40.0
37.5
35.0
-1
1
Interaction Plot (data means) for Vida
-1
1
-1
1
50
A
-1
1
40
A
30
50
B
-1
1
40
B
30
C
Se recomendaría utilizar el mayor valor de B y el mayor valor de C
Pagina 17 de 22
2006
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
Ejercicio 6.15
Se utiliza una aleación de níquel y titanio para fabricar componentes de los motores de
turbinas de aviones. La formación de fisuras es un problema potencialmente serio de las
piezas terminadas, ya que pueden provocar fallas irreversibles. Se realiza una prueba de
las piezas para determinar el efecto de cuatro factores sobre las fisuras. Los cuatro
factores son la temperatura de vaciado (A), el contenido de titanio (B), el método de
tratamiento térmico (C) y la cantidad de refinador de grano usada (D). se hacen dos
réplicas de un diseño 24 y se mide la longitud de las fisuras (en mm x 10-2) inducidas en un
ejemplar de prueba de muestra sometido a una prueba estándar. Los datos se muestran
en la siguiente tabla:
A
+
+
+
+
+
+
+
+
B
C
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
D
+
+
+
+
+
+
+
+
Combinación de
tratamientos
(1)
a
b
ab
c
ac
bc
abc
d
ad
bd
abd
cd
acd
bcd
abcd
Réplica
I
7.037
14.707
11.635
17.273
10.403
4.368
9.360
13.440
8.561
16.867
13.876
19.824
11.846
6.125
11.190
15.653
II
6.376
15.219
12.089
17.815
10.151
4.098
9.253
12.923
8.951
17.052
13.658
19.639
12.337
5.904
10.935
15.053
Creación del Diseño
Full Factorial Design
Factors:
Runs:
Blocks:
4
32
1
Base Design:
Replicates:
Center pts (total):
4, 16
2
0
a) Estimar los efectos de los factores ¿Qué efectos de los factores parecen ser
grandes?
Factorial Fit: Fisura versus Vaciado (A), Titanio (B), ...
Estimated Effects and Coefficients for Fisura (coded units)
Term
Constant
Vaciado (A)
Titanio (B)
T. Termico (C)
Grano (D)
Pagina 18 de 22
2006
Effect
3.019
3.976
-3.596
1.958
Coef
11.988
1.509
1.988
-1.798
0.979
SE Coef
0.05036
0.05036
0.05036
0.05036
0.05036
T
238.04
29.97
39.47
-35.70
19.44
P
0.000
0.000
0.000
0.000
0.000
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
Vaciado (A)*Titanio (B)
Vaciado (A)*T. Termico (C)
Vaciado (A)*Grano (D)
Titanio (B)*T. Termico (C)
Titanio (B)*Grano (D)
T. Termico (C)*Grano (D)
Vaciado (A)*Titanio (B)*
T. Termico (C)
Vaciado (A)*Titanio (B)*Grano (D)
Vaciado (A)*T. Termico (C)*Grano (D)
Titanio (B)*T. Termico (C)*Grano (D)
Vaciado (A)*Titanio (B)*
T. Termico (C)*Grano (D)
S = 0.284885
R-Sq = 99.77%
1.934
-4.008
0.076
0.096
0.047
-0.077
3.137
0.967
-2.004
0.038
0.048
0.024
-0.038
1.569
0.05036
0.05036
0.05036
0.05036
0.05036
0.05036
0.05036
19.20
-39.79
0.76
0.95
0.47
-0.76
31.15
0.000
0.000
0.459
0.355
0.645
0.456
0.000
0.098
0.019
0.036
0.014
0.049
0.010
0.018
0.007
0.05036
0.05036
0.05036
0.05036
0.97
0.19
0.35
0.14
0.345
0.852
0.728
0.890
R-Sq(adj) = 99.56%
Normal Probability Plot of the Standardized Effects
(response is Fisura, Alpha = .05)
99
B
95
90
Percent
F actor
A
B
C
D
ABC
A
80
D
AB
70
Effect Ty pe
Not Significant
Significant
N ame
V aciado (A )
Titanio (B)
T. Termico (C )
G rano (D )
60
50
40
30
20
C
10
5
1
AC
-50
-40
Pagina 19 de 22
2006
-30
-20
-10
0
10
Standardized Effect
20
30
40
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
Pareto Chart of the Standardized Effects
(response is Fisura, Alpha = .05)
2.12
F actor
A
B
C
D
AC
B
C
ABC
N ame
V aciado (A )
Titanio (B)
T. Termico (C )
G rano (D )
A
Term
D
AB
ABD
BC
CD
AD
BD
BCD
A CD
A BCD
0
10
20
30
Standardized Effect
40
b) Conducir un análisis de varianza. ¿Algunos de los factores afecta la formación de
fisuras? Utilizar alfa = 0.05
Analysis of Variance for Fisura (coded units)
Source
Main Effects
2-Way Interactions
3-Way Interactions
4-Way Interactions
Residual Error
Pure Error
Total
DF
4
6
4
1
16
16
31
Seq SS
333.496
158.609
78.841
0.002
1.299
1.299
572.246
Adj SS
333.496
158.609
78.841
0.002
1.299
1.299
Adj MS
83.3740
26.4348
19.7103
0.0016
0.0812
0.0812
F
1027.28
325.71
242.86
0.02
P
0.000
0.000
0.000
0.890
Todos los factores son significativos en la formación de fisuras
c) Escribir un modelo de regresión que pueda usarse para predecir la longitud de las
fisuras como una función de los efectos principales y las interacciones significativas
que se han identificado en el inciso b.
yˆ  11.988 1.509A  3.976B  1.798C  0.979D  0.967AB  2.004AC  1.569ABC
Pagina 20 de 22
2006
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
d) Analizar los residuales de este experimento.
Al analizar las siguientes gráficas nos muestran que existe normalidad en los residuos y por lo
tanto el modelo es válido y existe independencia de los factores con la respuesta.
Normal Probability Plot of the Residuals
(response is Fisura)
99
95
90
Percent
80
70
60
50
40
30
20
10
5
1
-3
-2
-1
0
1
Standardized Residual
2
3
Residuals Versus the Fitted Values
(response is Fisura)
Standardized Residual
2
1
0
-1
-2
5.0
7.5
10.0
12.5
Fitted Value
15.0
17.5
20.0
e) ¿hay algún indicio de que alguno de los factores afecte la variabilidad de la
formación de fisuras?
f)
¿Qué recomendaciones se harían respecto de las operaciones del proceso?
Utilizar gráficas de las interacciones y/o de los efectos principales como ayuda
para sacar conclusiones.
Pagina 21 de 22
2006
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,
Diseño de Experimentos factoriales
Main Effects Plot (data means) for Fisura
Vaciado (A)
14
Titanio (B)
13
Mean of Fisura
12
11
10
-1
1
-1
T. Termico (C)
14
1
Grano (D)
13
12
11
10
-1
1
-1
1
Interaction Plot (data means) for Fisura
-1
1
-1
1
-1
1
16
Vaciado (A)
12
Vaciado (A)
-1
1
8
16
Titanio (B)
12
Titanio
(B)
-1
1
8
16
T. Termico (C)
12
8
T.
Termico
(C)
-1
1
Grano (D)
De las anteriores gráficas se puede sugerir que para minimizar las fisura es necesario aplicar
el menor valor de A (vaciado), el menor vaciado de B (titanio), y el menor valor de C
(Tratamiento térmico), así como el menor valor de D (refinador de grano) .
Pagina 22 de 22
2006
Profesor: Dr. Primitivo Reyes Aguilar
Alumna: Lic. Esperanza Jiménez Becerril
Febrero 23,