11 - Web del Profesor
Anuncio
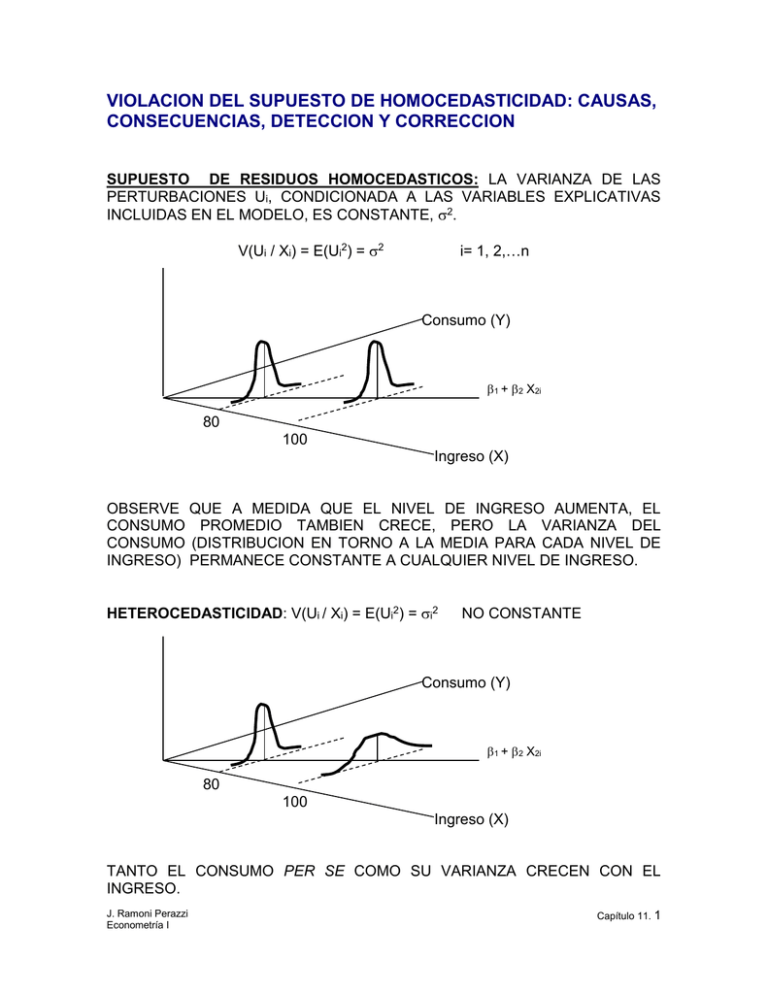
VIOLACION DEL SUPUESTO DE HOMOCEDASTICIDAD: CAUSAS, CONSECUENCIAS, DETECCION Y CORRECCION SUPUESTO DE RESIDUOS HOMOCEDASTICOS: LA VARIANZA DE LAS PERTURBACIONES Ui, CONDICIONADA A LAS VARIABLES EXPLICATIVAS INCLUIDAS EN EL MODELO, ES CONSTANTE, 2. V(Ui / Xi) = E(Ui2) = 2 i= 1, 2,…n Consumo (Y) 1 + 2 X2i 80 100 Ingreso (X) OBSERVE QUE A MEDIDA QUE EL NIVEL DE INGRESO AUMENTA, EL CONSUMO PROMEDIO TAMBIEN CRECE, PERO LA VARIANZA DEL CONSUMO (DISTRIBUCION EN TORNO A LA MEDIA PARA CADA NIVEL DE INGRESO) PERMANECE CONSTANTE A CUALQUIER NIVEL DE INGRESO. HETEROCEDASTICIDAD: V(Ui / Xi) = E(Ui2) = i2 NO CONSTANTE Consumo (Y) 1 + 2 X2i 80 100 Ingreso (X) TANTO EL CONSUMO PER SE COMO SU VARIANZA CRECEN CON EL INGRESO. J. Ramoni Perazzi Econometría I Capítulo 11. 1 CAUSAS DE HETEROCEDASTICIDAD: MODELOS DE ENSAYO Y ERROR: LA EXPERIENCIA REDUCE LOS ERRORES DE COMPORTAMIENTO EN EL TIEMPO, O EN COMPARACION CON LOS MENOS EXPERIMENTADOS VARIANZA DECRECE (SECRETARIAS, OPERADORES DE MAQUINARIAS, …) INGRESO DISCRECIONAL: A MENOS INGRESO, MAYOR PMgC. PERSONAS CON BAJOS RECURSOS TIENDEN A GASTAR TODO SU INGRESO (AHORRO 0). PERSONAS CON MAS ALTO NIVEL DE INGRESO TIENEN MAS OPCIONES EN CUANTO A COMO DISTRIBUIR SU INGRESO VARIANZA CRECE. Salarios (COM) como función del tamaño de empresa (NE) 7000 6000 COM 5000 4000 3000 2000 1000 0 2 4 6 8 10 NE MEJORAS EN LOS SISTEMAS DE RECOLECCION DE DATOS MALA ESPECIFICACION DEL MODELO DE REGRESION: FORMA FUNCIONAL INCORRECTA, OMISION DE VARIABLES RELEVANTES. ASIMETRIA EN LA DISTRIBUCION DE VARIABLES EXPLICATIVAS INCLUIDAS EN EL MODELO (INGRESO, RIQUEZA, EDUCACION, ETC) MANIPULACION DE LOS DATOS: INCORRECTA TRANSFORMACION DE LOS DATOS (DIFERENCIAS O RAZONES). J. Ramoni Perazzi Econometría I Capítulo 11. 2 OUTLIERS O FACTORES ATIPICOS: OBSERVACIONES QUE SON MUY DIFERENTES CON RESPECTO AL RESTO DE LA MUESTRA Consumo como función del ingreso para distintos países OUTLIER (Chile) 1000 EXPEND 800 600 400 200 0. 4 0. 6 0. 8 1. 0 1. 2 I NC NOTA: LOS PROBLEMAS DE HETEROCEDASTICIDAD SON MAS FRECUENTES EN DATOS DE CORTE TRANSVERSAL (INDIVIDUOS, EMPRESAS, PAISES… DE DIFERENTE TAMAÑO, CONDICION, ETC). DISTINTOS INDIVIDUOS O UNIDADES EN UN PUNTO DADO DEL TIEMPO TIENDEN A SER MAS HETEROGENEOS. EN SERIES DE TIEMPO LAS VARIABLES TIENDEN A PRESENTAR MAGNITUDES SIMILARES EN EL TIEMPO POR EL EFECTO AGREGACIÓN. CONSECUENCIAS DE LA HETEROCEDASTICIDAD: EN PRESENCIA DE HETEROCEDASTICIDAD, LOS ESTIMADORES MCO SERAN LINEALES, INSESGADOS Y CONSISTENTES ( β̂ i n>> i) PERO NO EFICIENTES. DEJAN DE SER MELI. LA VARIANZA NO ES MINIMA EN EFECTO, PARA EL MODELO: J. Ramoni Perazzi Econometría I LOS RESULTADOS DE LAS PRUEBAS t Y F NO SON CONFIABLES Yi = 1 + 2 Xi + Ui Capítulo 11. 3 VAR ( β̂ 2) = VAR ( β̂ 2) = σ2 x 2i x ( x CON HOMOCEDASTICIDAD 2 2 2i σi 2 2i 2 )2 CON HETEROCEDASTICIDAD DETECTANDO HETEROCEDASTICIDAD: NATURALEZA DEL PROBLEMA: DATOS CORTE TRANSVERSAL: A MAYOR HETEROGENEIDAD DE LA MUESTRA, MAYOR PROBABILIDAD DE HETEROCEDASTICIDAD. METODO GRAFICO: EXAMEN POSTMORTEM DE LOS RESIDUOS AL CUADRADO EN BUSCA DE PATRONES SISTEMATICOS ( û i usados como proxies de ui) û i 2 vs Ŷi INFORMACION GENERAL û i 2 vs Xi INFORMACION ESPECIFICA J. Ramoni Perazzi Econometría I Capítulo 11. 4 METODOS FORMALES: EXISTE UNA VARIEDAD DE TEST DE HETEROCEDASTICIDAD, TODOS ELLOS BASADOS EN DETERMINAR SI EXISTE O NO ALGUN TIPO DE RELACION ESTADISTICAMENTE SIGNIFICATIVA ENTRE LOS RESIDUOS Y ALGUNA OTRA VARIABLE. LOS PRIMEROS TESTS, COMO EL DE PARK Y GLEJSER RESULTAN POCO CONFIABLES DADO QUE NADA GARANTIZA QUE LOS RESIDUOS DE LAS REGRESIONES SOBRE LOS QUE SE BASAN SEAN A SU VEZ HETEROCEDASTICOS. SIN EMBARGO, ESTOS TESTS SIRVIERON DE BASE PARA OTROS MÀS ROBUSTOS Y DE USO MÁS FRECUENTE ACTUALMENTE: HETEROCEDASTICIDAD IMPLICA QUE EXISTE UMA RELACION ENTRE LA VARIANZA DE LOS RESIDUOS Y UNA O MAS VARIABLES DENTRO O FUERA DEL MODELO. DE ALLI QUE EL OBJETIVO DE TODOS ESTOS TESTS SEA PROBAR SI EXISTE O NO TAL RELACION-. . 1. TEST BREUSCH-PAGAN-GODFREY1: SEA Yi = 1 + 2 X2i + ... + k Xki +ui ASUMA i2 = 1 + 2 Z2i + … + m Zmi + vi DONDE LAS VARIABLES Zs PUEDEN SER O NO LAS MISMAS VARIABLES Xs. SE LLEVA A CABO UNA PRUEBA DE SIGNIFICACION CONJUNTA COMO SIGUE: H0: 2 = … = m = 0 RESIDUOS HOMOCEDASTICOS H1: AL MENOS UN 0 RESIDUOS HETEROCEDASTICOS PASOS: i) ii) iii) iv) v) ESTIME EL MODELO Y OBTENGA LOS RESIDUOS û i s CALCULE σ̂ 2 = û i 2/n CONSTRUYA LA VARIABLE pi= û i 2 / σ̂ 2 REGRESE pi CONTRA LAS Zs Y OBTENGA LA SCReg CALCULE = SCReg/2 2m-1 DESVENTAJAS: EL TEST ES SENSIBLE AL SUPUESTO DE NORMALIDAD DE LOS RESIDUOS ui. 1 EXISTEN OTROS TEST DE HETEROCEDASTICIDAD: TEST DE CORRELACION DE SPEARMAN, GOLDFELD-QUANT, KOENKER-BASSETT, POR NOMBRAR ALGUNOS. J. Ramoni Perazzi Capítulo 11. 5 Econometría I 2. TEST GENERAL DE WHITE: SEA Yi = 1 + 2 X2i + 3 X3i +ui Y û i 2 =1 + 2 X2i + 3 X3i + 4 X2i2 + 5 X3i2 + 6 X2iX3i + ui H0: 2 = … = m = 0 RESIDUOS HOMOCEDASTICOS H1: AL MENOS UN 0 RESIDUOS HETEROCEDASTICOS PASOS: i) ii) iii) DESVENTAJAS: ESTIME EL MODELO Y OBTENGA LOS RESIDUOS û i s ESTIME LA REGRESION AUXILIAR REGRESSION û i 2 = f(X2i, X3i, X2i2, X3i2, X2iX3i ) Y OBTENGA EL R2. CALCULE nR2 2k-1 HAY QUE SER CUIDADOSOS AL APLICAR EL TEST A MODELOS CON MUCHOS REGRESORES MEDIDAS REMEDIALES: 1) UTILIZAR LA INFORMACION REFERIDA A LA DESIGUAL VARIABILIDAD DE LA VARIABLE DEPEDIENTE A) MINIMOS CUADRADOS GENERALIZADOS2: APLICAR MCO A VARIABLES TRANSFORMADAS DE MODO TAL QUE SATISFAGAN LOS SUPUESTOS SEA Yi = 1(1) + 2 X2i +ui CON VAR (ui) = i2 CONOCIDA3 DIVIDA LA ECUACION ENTRE i Yi /i = 1(1/i) + 2 (X2i /i) +(ui/i) Yi* = 1(1*) + 2 X2i* +ui* 2 CUANDO LOS MCG MINIMIZAN LA SUMA CUADRATICA DE LOS RESIDUOS PONDERADOS, (( û i/ i)2), SE LE CONOCEN COMO MINIMOS CUADRADOS PONDERADOS. 3 SI LA VARIANZA ES DESCONOCIDA, UTILICE LA VARIANZA ESTIMADA (MCG FACTIBLES) J. Ramoni Perazzi Capítulo 11. 6 Econometría I DONDE ui* SON HOMOCEDASTICOS VAR (ui*) = E(ui*)2 = E(ui/i)2 = (1/i)2 E(ui)2 = (1/i)2 (i2) = 1 CONSTANTE EN TERMINOS MATRICIALES: ˆ MCG=(X’-1X)-1X’-1y B) TRANSFORMACION DE WHITE PARA ERRORES ESTANDAR ROBUSTOS (REGRESION ROBUSTA) WHITE SUGIERE CORREGIR LA ESTIMACION DE LOS ERRORES ESTANDAR DE LOS ˆ COMO SIGUE: VAR( β̂ j) = n wˆ i 1 2 ji uˆ i2 n ( wˆ 2ji ) 2 i 1 DONDE ŵ j SON LOS RESIDUOS DE LA REGRESION AUXILIAR DE Xj CON RESPECTO A LOS DEMAS REGRESORES. VENTAJA: PERMITE OBTENER ESTIMADORES MELI SIN ALTERAR LAS ESTIMACIONES DESVENTAJA: IGNORA OTRAS POSIBLES FORMAS DE HETEROCEDASTICIDAD: V(Ui) = 2Xi2 V(Ui) = 2Xi V(Ui) = 2 [E(Yi)]2 2) REDUCIR LA DESIGUAL VARIABILIDAD DE LA VARIABLE DEPENDIENTE TRANSFORMACION LOGARITMICA DE LAS VARIABLES, LO CUAL REDUCE LA ESCALA Y POR ENDE LA DIFERENCIA ENTRE VALORES. DEFLACTAR LAS VARIABLES A PARTIR DE ALGUNA MEDIDA DE TAMAÑO J. Ramoni Perazzi Econometría I Capítulo 11. 7 EJEMPLO 1: SUELDOS EN FUNCION DE ANTIGUEDAD Y EDUCACION. Sueldo promedio de profesores sin título de doctorado, independientemente de su antiguedad Dependent Variable: SUELDO Method: Least Squares Included observations: 1796 C ANTIG ANTIG2 DOCTOR R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood F-statistic Prob(F-statistic) Coefficient Std. Error t-Statistic Prob. 1171633. 83698.63 -1320.920 35643.85 4229.935 105.3072 21392.34 32.87055 19.78722 -12.54349 18.67393 0.0000 0.0000 0.0000 0.0000 399479.1 0.510215 0.509395 386236.3 2.67E+14 -25650.52 622.2488 0.000000 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion Hannan-Quinn criter. Durbin-Watson stat 2215022. 551425.7 28.56851 28.58075 28.57303 2.043191 Los sueldos aumentan en promedio Bs. 83698 con cada año de experiencia, pero a una tasa decreciente (1320,92) Los doctores ganan en promedio Bs. 399479 más que los no doctores Heteroskedasticity Test: White F-statistic Obs*R-squared Scaled explained SS 70.22060 387.2763 356.7119 Prob. F(7,1788) Prob. Chi-Square(7) Prob. Chi-Square(7) 0.0000 0.0000 0.0000 Dependent Variable: SUELDO Method: Least Squares Included observations: 1796 White Heteroskedasticity-Consistent Standard Errors Covariance C ANTIG ANTIG2 DOCTOR R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood F-statistic Prob(F-statistic) J. Ramoni Perazzi Econometría I Coefficient Std. Error t-Statistic Prob. 1171633. 83698.63 -1320.920 399479.1 28518.22 4276.930 113.8430 21298.57 41.08366 19.56979 -11.60300 18.75614 0.0000 0.0000 0.0000 0.0000 0.510215 0.509395 386236.3 2.67E+14 -25650.52 622.2488 0.000000 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion Hannan-Quinn criter. Durbin-Watson stat 2215022. 551425.7 28.56851 28.58075 28.57303 2.043191 Capítulo 11. 8 EJEMPLO 2: DE NUEVO LOS VEHICULOS Dependent Variable: PRECIO Method: Least Squares Included observations: 93 Variable Coefficient Std. Error t-Statistic Prob. C DOMESTICO POTENCIA -0.127778 -3.061851 0.147522 1.837829 1.208065 0.011589 -0.069527 -2.534508 12.72898 0.9447 0.0130 0.0000 R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat 0.646517 0.638662 5.806422 3034.308 -294.0203 1.521892 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic) 19.50968 9.659430 6.387532 6.469229 82.30447 0.000000 White Heteroskedasticity Test: F-statistic Obs*R-squared 2.245308 8.612539 Probability Probability 0.070533 0.071548 Residuos heterocedásticos al 8% Dependent Variable: LOG(PRECIO) Included observations: 93 Variable Coefficient Std. Error t-Statistic Prob. C DOMESTICO LOG(POTENCIA) -2.464940 -0.104167 1.097530 0.334486 0.048544 0.068214 -7.369332 -2.145823 16.08951 0.0000 0.0346 0.0000 R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat 0.742607 0.736888 0.233229 4.895610 4.946833 1.575917 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic) 2.865452 0.454686 -0.041867 0.039829 129.8302 0.000000 White Heteroskedasticity Test: F-statistic Obs*R-squared J. Ramoni Perazzi Econometría I 1.026644 4.146409 Probability Probability 0.398104 0.386554 Capítulo 11. 9 EJEMPLO 3: DE NUEVO TASA DE ASESINATOS Dependent Variable: M Included observations: 44 Variable Coefficient Std. Error t-Statistic Prob. C D1 D2 Y 7.754432 2.042382 4.697114 -3.131790 2.987502 1.128044 1.330173 1.511907 2.595624 1.810551 3.531205 -2.071417 0.0131 0.0777 0.0011 0.0448 R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat 0.644531 0.617870 2.759365 304.5637 -104.9965 2.085119 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic) 5.402909 4.463791 4.954386 5.116585 24.17576 0.000000 Residuos homocedásticos White Heteroskedasticity Test: F-statistic Obs*R-squared J. Ramoni Perazzi Econometría I 1.358711 7.944225 Probability Probability 0.256813 0.242218 Capítulo 11. 10
