Aplicación - Impuestos

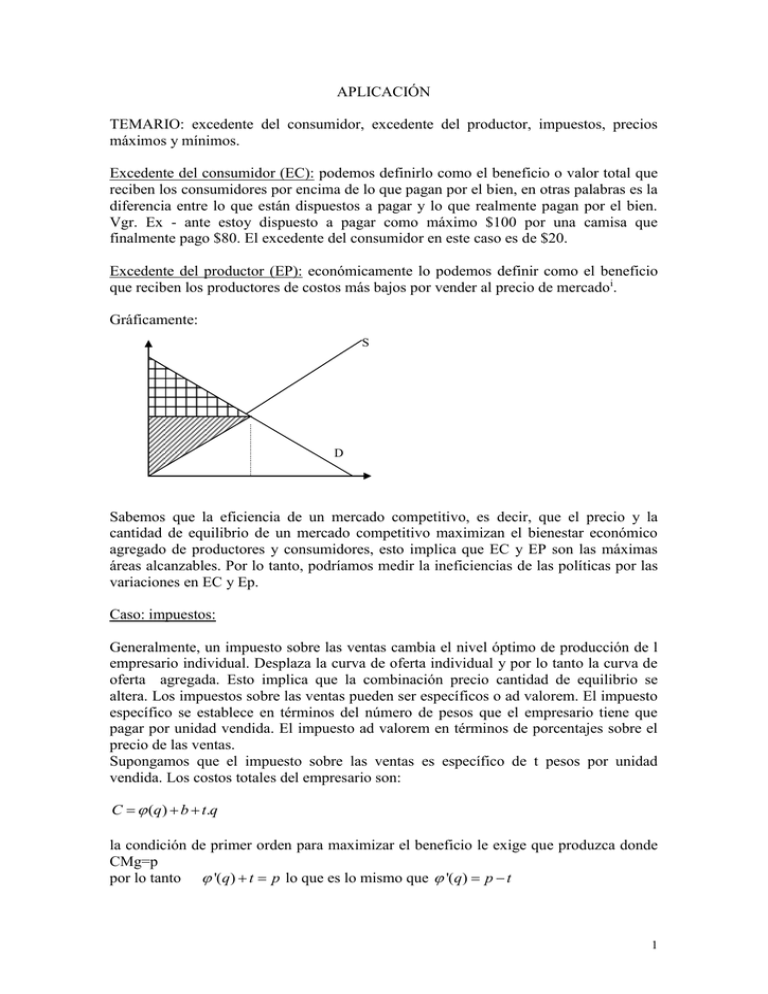
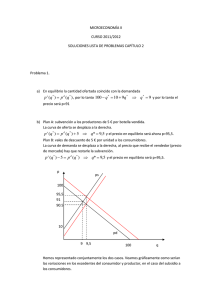
APLICACIÓN
TEMARIO: excedente del consumidor, excedente del productor, impuestos, precios
máximos y mínimos.
Excedente del consumidor (EC): podemos definirlo como el beneficio o valor total que
reciben los consumidores por encima de lo que pagan por el bien, en otras palabras es la
diferencia entre lo que están dispuestos a pagar y lo que realmente pagan por el bien.
Vgr. Ex - ante estoy dispuesto a pagar como máximo $100 por una camisa que
finalmente pago $80. El excedente del consumidor en este caso es de $20.
Excedente del productor (EP): económicamente lo podemos definir como el beneficio
que reciben los productores de costos más bajos por vender al precio de mercadoi.
Gráficamente:
S
D
Sabemos que la eficiencia de un mercado competitivo, es decir, que el precio y la
cantidad de equilibrio de un mercado competitivo maximizan el bienestar económico
agregado de productores y consumidores, esto implica que EC y EP son las máximas
áreas alcanzables. Por lo tanto, podríamos medir la ineficiencias de las políticas por las
variaciones en EC y Ep.
Caso: impuestos:
Generalmente, un impuesto sobre las ventas cambia el nivel óptimo de producción de l
empresario individual. Desplaza la curva de oferta individual y por lo tanto la curva de
oferta agregada. Esto implica que la combinación precio cantidad de equilibrio se
altera. Los impuestos sobre las ventas pueden ser específicos o ad valorem. El impuesto
específico se establece en términos del número de pesos que el empresario tiene que
pagar por unidad vendida. El impuesto ad valorem en términos de porcentajes sobre el
precio de las ventas.
Supongamos que el impuesto sobre las ventas es específico de t pesos por unidad
vendida. Los costos totales del empresario son:
C   (q)  b  t.q
la condición de primer orden para maximizar el beneficio le exige que produzca donde
CMg=p
por lo tanto  '(q)  t  p lo que es lo mismo que  '(q)  p  t
1
esto implica que el empresario iguala el costo marginal más el impuesto unitario al
precio. La función de oferta del empresario se obtiene hallando en el costo marginal el
valor de q para todos los precios mayores o iguales al costo medio variable, en símbolos
Si  S ( p  t ) .
La función de oferta agregada es sólo la suma de las ofertas individuales Si.
Por lo tanto la oferta agregada es función del precio neto (p-t) percibido por los
vendedores. Si en ausencia del impuesto la oferta agregada es de S0 unidades al precio
p0, los empresarios ofrecerán la misma cantidad con un impuesto de t pesos por unidad
si el precio pagado por los demandantes es p0+t pesos. Esto equivale a un
desplazamiento vertical de t pesos de la curva de oferta. Para hallar el equilibrio
hacemos D(p)=S(p-t) y encontramos p.
Para el caso de un impuesto ad valorem, si v es el porcentaje de impuesto, los costos
totales son:
C   (q)  b  v. p.q
igualando Cmg al precio:
 '(q)  vp  p re acomodando  '(q)  p.(1  v) por lo tanto la curva de oferta
individual es Si=Si[p.(1-v)] y la de oferta agregada la suma de las Si de 1 a n.
La oferta agregada es función del precio neto y el impuesto sobre las ventas implica un
desplazamiento hacia arriba de la curva de oferta proporcional a la elevación de la
curva de oferta original por encima del eje de las cantidades. De nuevo, la combinación
precio cantidad de equilibrio se determina haciendo la demanda igual a la oferta.
Ejemplo:
La industria consta de 100 empresas con funciones de costo idénticas:
Ci= 0,1.q2+q+10
Haciendo Cmg=p y despejando q y haciendo q=Si,
Si=0
si p<1
Si=5p-5
si p  1
Suponemos que la función de demanda es D=-400p+4000
Igualando la oferta a la demanda, obtenemos:
p*=5 y q*=2000
Supongamos que se establece un impuesto específico de t pesos, la función de costos
representativa es Ci=0,1q2+(1+t)q+10
igualando Cmg al precio y resolviendo tenemos que Si=5(p-t)-5 si p  1+t por lo que
S=500(p-t)-500 para el mismo rango de precios. Igualando la oferta a la demanda
obtenemos: p=5+5/9.t
si suponemos un impuesto de 0.9 centavos por unidad vendida obtenemos: p=5.5 y
q=1800
a consecuencia del impuesto aumenta el precio y disminuye la cantidad vendida. Pero el
alza del precio es menor que el aumento del impuesto por unidad. Los cincuenta
2
centavos de aumento en el precio son la porción del impuesto que se traslada al
consumidor, el resto, $0.40, es la carga que incide sobre el empresario. Las
proporciones que soporta cada una de las partes está estrechamente relacionado con la
elasticidad de cada una de las curvas. Vgr. cuánto más inelástica la demanda mayor
proporción pagan los consumidores.
p
t
5.5
5
1800 2000
q
Caso: control de precios
Se da cuando el gobierno obliga a los oferentes a cobrar un precio inferior al que
despeja el mercado vgr. Políticas de precios máximos en los ’70s y ’80s en la Argentina.
Grafico:
C
B
A
3
En este caso el beneficio de los consumidores es la diferencia entre A y B. la pérdida de
los productores es A+C. B+C mide la pérdida irrecuperable de eficiencia provocada por
los controles de precios.
Vale resaltar que si la demanda fuera más inelástica, los consumidores experimentarían
una pérdida de bienestar.
Grafico.
En este caso vimos que disminuye la eficiencia económica (el bienestar agregado de los
consumidores y productores cae).
No siempre la intervención gubernamental genera pérdidas de eficiencia, por ejemplo
cuando existen externalidades o fallas de mercado la intervención estatal puede ser
beneficiosa. Esto lo veremos al analizar equilibrio general.
Caso: precios mínimos: Se da cuando el gobierno obliga a los demandantes a pagar un
precio superior al que despeja el mercado. Por ejemplo: salarios mínimos, políticas de
precios agrícolas mínimos (vgr. juntas reguladoras).
Gráfico:
S
A
B
C
D
D
Q3
Q0
Q2
4
Se dan dos situaciones:
a) los productores creen que no colocarán más que q3, por lo que producirán q3 y la
pérdida de eficiencia será B+C.
b) si creen que pueden vender todo lo que quieran al Pmin producirán q2, por lo que la
cantidad ofrecida será q2 y la cantidad demandada q3, por lo que habrá un exceso de
oferta, esto es producción no vendida.
Por lo tanto:
La variación de EC=A+B, lo que pierden los que siguen comprando y que transfieren a
los oferentes (A) más lo que se pierde por los que dejaron de comprar (B).
Claramente EC es una pérdida.
La variación de EP=A-C-D, siendo D el costo de producir q2-q3 que es lo no vendido
(no debemos olvidar que por tratarse de mercados que tratamos como competitivos
suponemos que la curva de oferta es igual al costo marginal a partir de que este
sobrepasa al costo medio) y C representa el descenso de las ventas de q0 a q3.
Según qué tan grandes sean A,C,D el productor puede experimentar pérdidas netas.
Fuente
 “Teoría microeconómica”, Henderson – Quandt.
i
Es el equivalente económico del concepto contable de Margen bruto. Demostración:
0
excedente del productor 
 ( p  CMg ).dq  p.q * [CT (q*)  CT (0)]  p.q * CV (q*)
q*
5