feb 09 sol

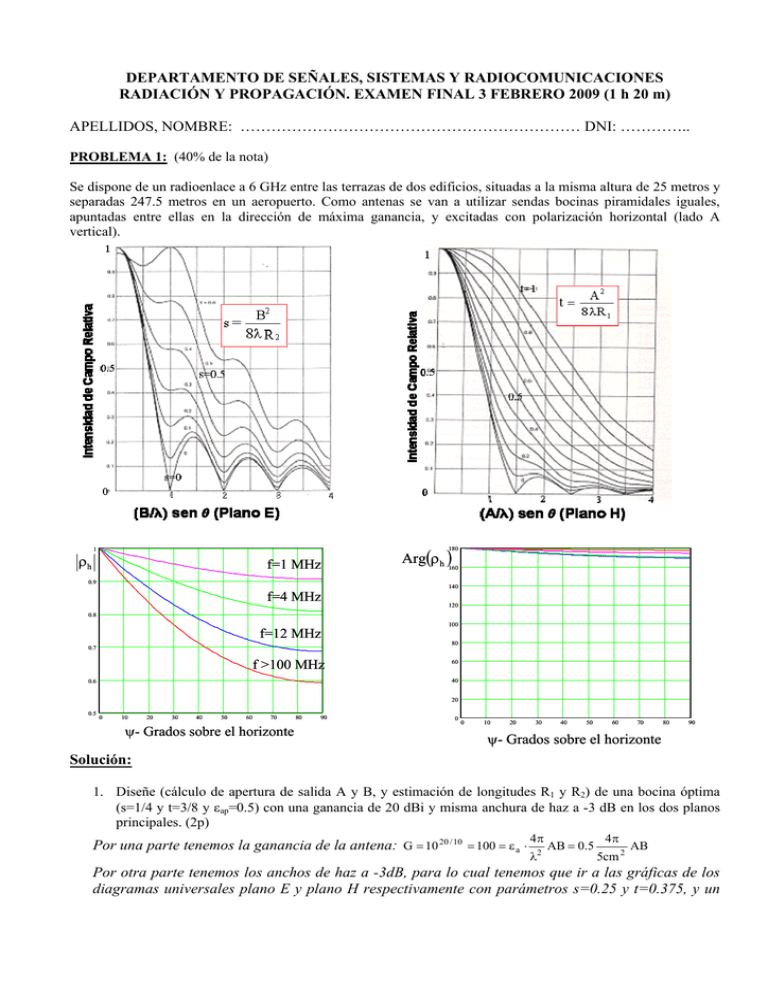
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 3 FEBRERO 2009 (1 h 20 m)
APELLIDOS, NOMBRE: ………………………………………………………… DNI: …………..
PROBLEMA 1: (40% de la nota)
Se dispone de un radioenlace a 6 GHz entre las terrazas de dos edificios, situadas a la misma altura de 25 metros y
separadas 247.5 metros en un aeropuerto. Como antenas se van a utilizar sendas bocinas piramidales iguales,
apuntadas entre ellas en la dirección de máxima ganancia, y excitadas con polarización horizontal (lado A
vertical).
ρh
Arg(ρ h )160
180
1
f=1 MHz
0.9
140
f=4 MHz
120
0.8
100
f=12 MHz
80
0.7
f >100 MHz
60
40
0.6
20
0.5
0
10
20
30
40
50
60
70
ψ- Grados sobre el horizonte
80
90
0
0
10
20
30
40
50
60
70
80
90
ψ- Grados sobre el horizonte
Solución:
1. Diseñe (cálculo de apertura de salida A y B, y estimación de longitudes R1 y R2) de una bocina óptima
(s=1/4 y t=3/8 y εap=0.5) con una ganancia de 20 dBi y misma anchura de haz a -3 dB en los dos planos
principales. (2p)
Por una parte tenemos la ganancia de la antena: G = 10 20 / 10 = 100 = ε a ⋅
4π
λ
2
AB = 0.5
4π
5cm 2
AB
Por otra parte tenemos los anchos de haz a -3dB, para lo cual tenemos que ir a las gráficas de los
diagramas universales plano E y plano H respectivamente con parámetros s=0.25 y t=0.375, y un
valor de ordenadas 10-3/20 = 0.71, obteniendo:
tiene que ser la misma (θ =BW/2) ⇒
B
A
senθ = 0.5 y
senθ = 0.7 . Como la anchura de haz
λ
λ
B 0.5
=
. Utilizando las dos ecuaciones con dos incógnitas, se
A 0.7
obtiene: A = 23.6 cm y B= 16.9 cm
2. Calcule la potencia recibida en dBm, en condiciones de espacio libre (sin considerar la reflexión en el
suelo), cuando se alimenta la bocina transmisora con una potencia de 1 mW. (2p)
Aplicando la fórmula de Friis: Prx (dBm) = Ptx (dBm) + G tx (dBi) − 20 log
4πd
+ G rx (dBi) . Para una potencia
λ
transmitida de 1 mW = 0 dBm, y con ganancias de ambas antenas de 20 dBi, se obtiene Prx=-55.9
dBm
3. Con la configuración real del radioenlace, calcule el ángulo de incidencia en el suelo y, con ayuda de la
gráfica adjunta, estime el coeficiente de reflexión en el suelo. (2p)
El ángulo de incidencia es:
α
25 m
25 m
α
α = a tan
25
= 11.4º
247.5 / 2
El valor del coeficiente de reflexión en el
suelo, para f>100 MHz y 11º, es ρ≈-0.9
247.5 m
4. Dibuje el diagrama de radiación en escala lineal y coordenadas cartesianas, en el margen angular de ±50º,
en el plano H, calculando el nivel de campo correspondiente al ángulo de incidencia, a 25º y a 50º. (2p)
Se trata de hacer el cambio de variable en abcisas
correspondiente al diagrama universal plano H
1
con t=3/8≈0.4, de
t=0.375
A
23.6cm
sin θ =
sin θ
λ
5cm
a los valores
de θ solicitados (11.4º, 25º y 50º)
0.55
0.17
0.04
11.4º
25º
50º
θ
Intensidad relativa de campo
5. Calcule las pérdidas o ganancia que en el radioenlace real produce el efecto de reflexión en el suelo,
respecto de la propagación en espacio libre. Debe tener en cuenta el diagrama de radiación de las antenas
y el efecto de la diferencia de caminos. (2p)
Para tener en cuenta la reflexión hay que considerar los siguientes fenómenos:
- Efecto de la reflexión en el suelo: ρ=-0.9
- Efecto de los diagramas de las antenas transmisora y receptora en el rayo reflejado: 0.55 x 0.55
- Efecto de la diferencia de amplitud por caminos: despreciable en este caso.
−j
2π
5m
- Efecto de la diferencia de fase por caminos respecto al rayo directo: e− jko∆R = e 5cm = 1
En total, el efecto es: 20 log (1-0.9x0.55x0.55)=-2.8 dB (atenuación de 2.8 dB respecto al caso ideal
sin reflexión)
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 3 FEBRERO 2009
APELLIDOS, NOMBRE: ………………………………………………………… DNI: …………..
PROBLEMA 2: (20% de la nota)
Considere la antena Yagi de la figura funcionando a una frecuencia de 300 MHz.. Haga la aproximación de que
las dos antenas son iguales y de longitud 2l=λ/2 tanto para estimar la impedancia mutua como para el cálculo del
campo radiado por ambos dipolos. La utilización de complejos en módulo y argumento es recomendable para
facilitar los cálculos. La expresión del campo del dipolo λ/2 situado sobre el eje z es:
r
E = j60I in
⎛π
⎞
cos⎜ cos θ ⎟ − jk r
2
⎝
⎠e o ˆ
θ
sin θ
r
y=20 cm
2l2 =51 cm
2l1 =44.5 cm
2a=6.35 mm 2a=6.35 mm
Curvas de autoimpedancia de dipolos
Solución:
1. Calcule la impedancia de entrada de la antena. (5p)
Tal como se hace en el ejemplo 4.3 del libro, (que casi es el mismo que el problema propuesto), como el
segundo dipolo está en cortocircuito, se puede imponer: V2=0, con lo que la impedancia activa vista desde la
puerta 1 vale:
V1 = Z11I1 + Z12 I2 ⎫
V1
Z2
= Z11 − 12
⎬ ⇒ Zin =
0 = Z21I1 + Z22I 2 ⎭
I1
Z22
z
#2
#1
V2=0
Máxima radiación
V1
Activo
Reflector
Para obtener los valores de autoimpedancias:
λ=100 cm y 2a = 6.35 mm: a/λ = 0.003175
2L1 = 44.5 cm → koL1 = 2πL1/λ =1.4
2L2 = 51 cm → koL2 = 2πL2/λ =1.6
Z11 = 58-38j
Z22 = 90 + 50j = 103 ∠29º
Para obtener la impedancia mutua (considerando,
de acuerdo con el enunciado), que 2L1≈2L2≈ λ/2:
Z12=Z21=50-20j=53.85 ∠-21.8º
La impedancia de entrada resulta:
Zin = 58-38j-28.15∠-72.6º=49.6-11.1j
2. Fije un sistema de coordenadas sobre la antena y diga cuál es la dirección de máxima radiación. Estime la
directividad de la antena. (5p)
La dirección de máxima radiación en una Yagi es la de la dirección que ocupan los elementos
directores o, como en nuestro caso, la opuesta a la dirección del elemento reflector. Para el cálculo de
la directividad, hay que calcular el campo primero en dicha dirección, y luego aplicar la definición de
directividad, (tal como se hizo en el ejemplo 4.3 y en el ejercicio propuesto 4.6). El campo se calcula
como la suma del campo generado por los dos elementos, que de acuerdo con el enunciado se pueden
suponer iguales a λ/2:
r
ET
π⎞
π⎞
⎛π
⎛π
cos⎜ cos ⎟ − jk (r + 20cm )
cos⎜ cos ⎟ − jk r
o
I
I
2⎠ e o
2⎠ e
60
60
⎝2
⎝2
I1 1 + 2 e − jk o 20cm =
=
I1 1 + 2 ∠ − 72º
+ j60I 2
= j60I1
π
π
r
r
I1
I1
r
r
sin
sin
2
2
Donde
I2
Z
= − 12
I1
Z 22
r
= 0.52∠129.2 , con lo que E T
2
2
2
⎛ 60
⎞
⎛ 60 ⎞
= ⎜ I1 1 + 0.52∠57.2º ⎟ = ⎜ I1 ⎟ 2.12
⎝ r
⎠
⎝ r ⎠
2
2
La directividad se obtiene como: D =
ET
4πr 2
4πr 2
4πr 2
S =
=
1 2
Prad
2 ⋅120π 1 2
I1 R in
I1 49.6
2
2
⎛ 60 ⎞
⎜ I1 ⎟ 2.12
⎝ r
⎠
= 5.13 ⇒ 7.1 dBi
2 ⋅120π
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 3 FEBRERO 2009
APELLIDOS, NOMBRE: ………………………………………………………… DNI: …………..
TEORÍA: (30 minutos) (40% de la nota)
Instrucciones: responda de manera breve y concisa, en el espacio asignado, a cada pregunta. No es necesario realizar ningún
cálculo (deje las operaciones indicadas) por lo que no está permitido utilizar calculadora.
1. Haga un esquema del balun tipo Bazooka o Sleeve y explique su funcionamiento (0.5p)
El balun tipo bazooka tiene como objetivo simetrizar las corrientes en los
dos brazos del dipolo. Para ello se construye una línea coaxial concéntrica
con el conductor exterior del cable coaxial de partida, de longitud λg/4, que
se cortocircuita en su extremo inferior, dando lugar así a un circuito
abierto en el extremo superior. Este circuito abierto evita que fluya
corriente por la parte exterior del cable coaxial.
2. Explique el funcionamiento de las antenas de onda progresiva, dibuje algún ejemplo y diga en qué banda
se suelen utilizar (0.5 p)
Las antenas de onda progresiva se suelen utilizar en
HF, y se construyen con hilos conductores largos, que
soportan ondas progresivas de corriente. Para ello,
necesitan cargarse en su extremo con una resistencia
terminal que evita la onda reflejada. Además del
ejemplo de la figura, también son de onda progresiva
las antenas en V y las rómbicas. La antena de hélice
también funciona como antena de onda progresiva,
aunque en este caso no se carga porque la corriente
que llega al extremo es muy pequeña.
3. Se tienen dos bocinas piramidales de la misma ganancia, una óptima y otra de bajo error de fase. Diga
cuál es la más corta de las dos y cuál tiene la apertura más grande. (0.5p)
La bocina más corta es la óptima (con errores de fase s=1/4 y t=3/8), por la propia definición de
bocina óptima. Sin embargo, la eficiencia de estas antenas es menor (ε=0.5), con lo que para tener
la misma ganancia es necesario que tengan una apertura mayor.
4. Explique por qué en los arrays endfire la separación entre elementos no debe superar típicamente 0.42λ
(0.5p)
Para evitar el grating lobe (o lóbulo de difracción emergente) que aparece en la dirección
opuesta a la dirección de máxima radiación cuando la separación entre elementos es mayor. Por
ejemplo, si la separación entre elementos es de 0.5λ el diagrama se hace bidireccional con máximos
de igual amplitud en los dos sentidos de la recta del array.
5. Diga en qué planos (principales o diagonales) la radiación contrapolar de un reflector es más alta y por
qué. (0.5p)
La radiación contrapolar es más alta en los planos diagonales, tal como aparece en los diagramas
típicos de los reflectores mostrados en clase. De hecho en los planos principales, los campos contrapolares
radiados por los distintos cuadrantes de la apertura se compensan.
6. Para una comunicación por onda ionosférica entre dos puntos separados 3000 km, diga si la óptima
frecuencia utilizable debe ser mayor a medianoche o a mediodía y por qué. (0.5p)
La óptima frecuencia utilizable es 0.85 MUF. Como la máxima frecuencia utilizable es a su vez
proporcional a la frecuencia crítica de la capa F2, y ésta depende de la densidad máxima de electrones de
dicha capa, la frecuencia óptima será mayor a mediodía que a medianoche, puesto que a medianoche la
densidad de electrones baja por la ausencia de ionización debida al Sol.
7. Se dispone de una antena reflectora offset con una relación F/D = 0.7 y diámetro de apertura proyectada
de 1 metro, con una bocina cónica corrugada diseñada para máxima ganancia. A causa del viento la
antena se cae y se estropea el reflector. Se quiere aprovechar el mismo alimentador para iluminar un
nuevo reflector capaz de dar 3 dB menos de ganancia. Diga cómo diseñaría el nuevo reflector (diámetro
del reflector y distancia focal) (0.5p)
Al utilizar el mismo alimentador, si se quiere mantener la condición de máxima ganancia, el ángulo θo
del nuevo reflector debe ser el mismo, lo que implica que hay que mantener constante la relación F/D. Si se
quiere reducir la ganancia en 3 dB, el área de la apertura se deberá reducir a la mitad, por lo que el
diámetro se reducirá en un factor √2. La distancia focal, por lo tanto, también se reducirá en la misma
proporción√2:
8. “Como antenas de un radioenlace a 800 MHz se utilizan Yagis de 15 dBi de ganancia”. Comente
detalladamente (explicando las causas) si la frase es correcta y/o contiene incongruencias. (0.5p)
La frase es correcta ya que 800 MHz es una banda de frecuencia típica para las antenas Yagi (de hecho
esta frecuencia pertenece a la banda de emisión de TV terrestre donde se utilizan Yagis). También los 15 dBi
de ganancia es un valor típico para antenas con 10/12 directores.