Examen ordinario de Análisis Dinámico de Sistemas Mecánicos Curso 2000-2001 1 Parcial
Anuncio

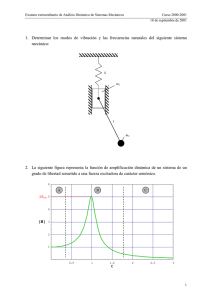
Examen ordinario de Análisis Dinámico de Sistemas Mecánicos Curso 2000-2001 er 1 Parcial 3 de febrero de 2001 CUESTIONES 1. La siguiente figura representa la función de amplificación dinámica de un sistema de un grado de libertad sometido a una fuerza excitadora de carácter armónico. 6 A B C |H|máx 5 4 »H» 3 2 1 0.5 1 1.5 τ 2 2.5 3 Indique cuáles de las siguientes afirmaciones son ciertas: a) Para τ = 0 las fuerzas de inercia son nulas. b) Para τ → ∞ todas las fuerzas son nulas, por eso |H| tiende a cero. c) Para τ = 1, las fuerzas de inercia y las fuerzas elásticas son nulas, por eso en la zona B dominan la fuerza de amortiguamiento. d) En la zona C dominan las fuerzas de inercia y en A las elásticas. e) Cuanto mayor sea el coeficiente de amortiguamiento (ξ) mayor será el máximo la función de amplificación dinámica (|H|máx). f) Ninguna de las anteriores. Examen ordinario de Análisis Dinámico de Sistemas Mecánicos Curso 2000-2001 er 1 Parcial 3 de febrero de 2001 2. En el sistema de la figura, la fuerza transmitida a la base viene dada por la expresión: a) m( x − y) F(t) b) k ( x − y ) x(t) c) kx + F (t ) m d) F (t ) − m( x − y) e) Ninguna de las anteriores k/2 k/2 y(t) Tiempo: 30 minutos Examen ordinario de Análisis Dinámico de Sistemas Mecánicos Curso 2000-2001 er 1 Parcial 3 de febrero de 2001 PROBLEMA En una fábrica de munición para armas ligeras (distinta de la que apareció en el examen parcial), cada partida de balas debe pasar unos controles de calidad consistentes en el disparo de un cierto número de ellas. Dado que se fabrica una gran variedad de balas, la diana de la que se dispone para la realización de los ensayos (que se muestra en la figura) puede usarse para ensayar balas con diferentes masas y velocidades de impacto. Para ello, incorpora un sistema que permite variar la pretensión del muelle. x ∆ l m v0 k M Determinar la pretensión del muelle (δp) necesaria para ensayar una bala de masa m= 1,8·10-2 kg y velocidad de impacto v0= 300 m/s, si la condición de diseño es que la parte móvil de la diana no tope con la parte fija (xmáx<∆). Datos: − Masa de la parte móvil de la diana: M= 3 kg − Rigidez del muelle: k= 1000 N/m − Desplazamiento máximo de la parte móvil de la diana: ∆= 0,05 m Nota: − Después del impacto la bala permanece unida a la diana. Tiempo: 30 minutos Examen ordinario de Análisis Dinámico de Sistemas Mecánicos Curso 2000-2001 2º Parcial 3 de febrero de 2001 PROBLEMA En el sistema de la figura, y(t) k1 F(t) x(t) m1 z(t) c1 θ(t) k2 m (x)= µ k3 m2 w(t) c2 a a 2a si suponemos que la variación de θ(t) es pequeña e y(t), z(t), w(t) y F(t) son funciones del tiempo conocidas, se pide: 1. Obtener las expresiones de la energía cinética, la energía potencial y la función de disipación de Rayleigh. 2. Obtener las ecuaciones de movimiento del sistema, en función de m1, m2, µ, k1, k2, k3, c1, c2, a, x(t), θ(t), y(t), z(t), w(t) y F(t) aplicando las ecuaciones de Lagrange. 3. Si: − m1=m2= 1 kg, − µ= 1 kg/m, − k1=k2=k3= 1 N/m y − a= 1 m, Calcular las frecuencias naturales del sistema. 4. Obtener los modos de vibración asociados a cada una de las frecuencias naturales calculadas en el apartado anterior. Nota: − R2 << a. Tiempo: 50 minutos