EJERCICIO RESUELTO DE PROPAGACIÓN.
Anuncio

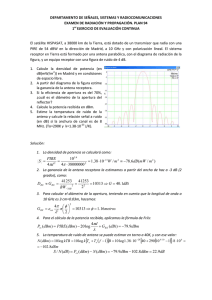
EJERCICIO RESUELTO DE PROPAGACIÓN. Un sistema de radiocomunicaciones tiene los siguientes parámetros: f PT fT,R AeT,R d = 26 GHz = 1W = 2 dB, atenuación de las guías en TX y RX = 0,02 m2, apertura equivalente de la antena en TX y RX = 2 Km. Distancia entre el transmisor y el receptor 1.- Determinar la intensidad de campo en el Espacio libre en el punto de recepción: Calculamos en primer lugar los valores de otros parámetros necesarios: c 3·108 0,0115m f 26·109 PT = 0 dBW = 30 dBm; E EL 30 G T ,R fT,R 4A e 1900veces 32,76 dB 2 = 102/10 = 1,58 veces PT g T T 0,09 (V / m) E EL 20·log E(V / m)·106 99,08 (dBV / m) d E (dB/μ V/m) = 74,8+ 10logPT (w) 20logd (km) G T fT 99,08(dBV / m) 2.- Determinar la densidad de potencia en el Espacio libre en el punto de recepción: EL E2 0,092 2,15·105 ( w / m 2 ) EL 10·log ( w / m 2 46,6 (dBw / m 2 ) 120· 120· 3.- Determinar la atenuación en el Espacio libre en el punto de recepción y a partir de ella la potencia recibida: A EL 32,45 20·logf (MHz) 20logd (Km) 126,77 (dB) PR EL (dBm) PT (dBm) G T G R A EL fT fR 35,21 (dBm) 4.- Comprobar que a partir de los valores de intensidad de campo y densidad de potencia y usando las fórmulas de recepción (teniendo en cuenta la apertura o ganancia de la antena y las pérdidas en el alimentador de recepción) se obtiene el mismo resultado para la potencia recibida. 5.- Calcular la atenuación por gases ( = 10 g/m3) y la potencia recibida ahora: 7,27 2 7,5 3 3 o 2 f 10 7,26·10 (dB / Km) 2 f 0,35 f 57 2,44 3,27102 1,67103 7,7104 f 0,5 2 w f 10 4 0,145 (dB / Km) 3,79 f 22,232 9,81 PR PR,EL Ag 35,51 (dBm) Ag ( O W ) ·d (Km) 0,3 (dB) 6.- Calcular la atenuación por lluvia para el 0,01 % del tiempo con polarización horizontal (R = 35 mm/H; = 0,124; = 1,061) y la potencia recibida si en ese momento estuviera lloviendo con esa intensidad: R k (R ) 0,124(35) 1,061 5,39 (dB / km) 1 r0,01 0,912 LE d ·r0,01 1,82 Km 1 LR / L0 A(0,01%) R ·LE (km) 9,83 dB PR PR,EL Ag All 45,34 (dBm) 7.- Para el siguiente perfil determinar la atenuación por difracción y la potencia recibida considerando todos los fenómenos anteriores. h x 30 m 30 m 50 m 1,5 Km 1,5 Km 0,5 Km 30 20 x ; x 2,5 m ; h 50 20 x 27,5 m 2 0,5 =h 2 (d1 + d2) 2 (2000) 27,5 18,72 d1 d2 0,0115·1500·500 A( ) = 6.9 + 20 log 20 m 20 m ( 0,1) 2 + 1 + 0,1 38,33 dB PR PR, EL Ag All AD 83,67 (dBm) 0,5 Km