Clase práctica.
Anuncio
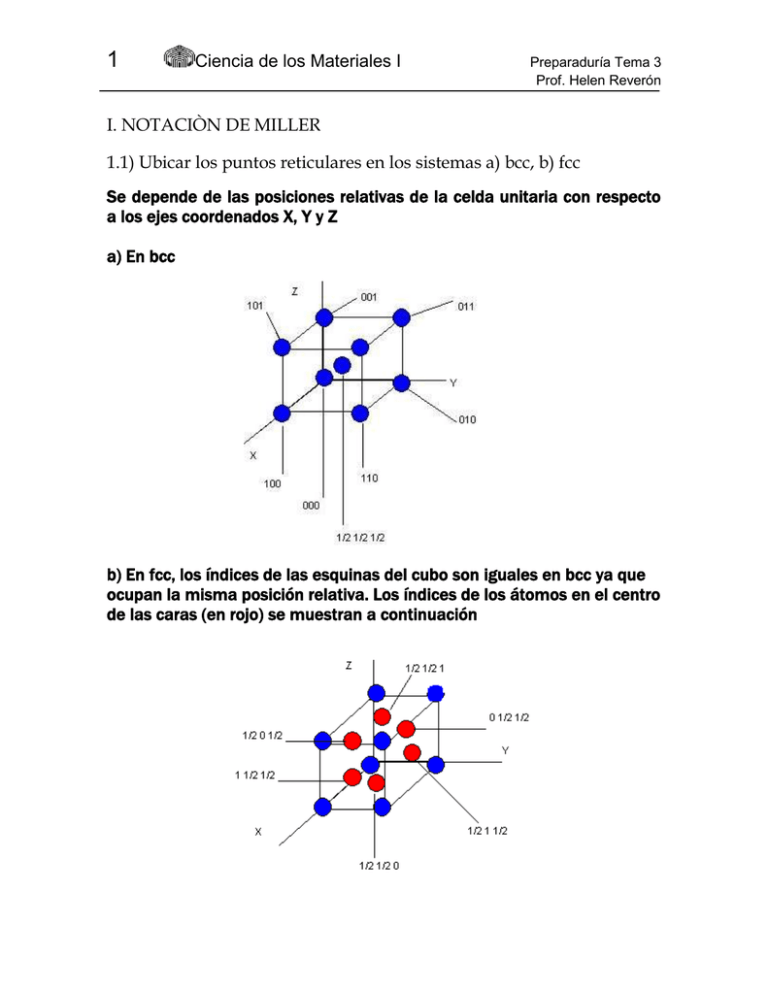
1 Ciencia de los Materiales I Preparaduría Tema 3 Prof. Helen Reverón I. NOTACIÒN DE MILLER 1.1) Ubicar los puntos reticulares en los sistemas a) bcc, b) fcc Se depende de las posiciones relativas de la celda unitaria con respecto a los ejes coordenados X, Y y Z a) En bcc b) En fcc, los índices de las esquinas del cubo son iguales en bcc ya que ocupan la misma posición relativa. Los índices de los átomos en el centro de las caras (en rojo) se muestran a continuación 2 Ciencia de los Materiales I Preparaduría Tema 3 Prof. Helen Reverón 1.2)Direcciones a) ¿Qué puntos reticulares caen a lo largo de la dirección [111] en las celdas unitarias bcc, tetragonal centrada en el cuerpo y ortorrómbica centrada en el cuerpo? En las tres estructuras, la dirección [111] es una diagonal que atraviesa toda la celda y pasa por el centro. Así en las tres estructuras, se tocan los puntos 000; ½ ½ ½ ; 111 b) Identificar la familia de direcciones <100> [100] [100] [010] [010] [001] [001] 3 Ciencia de los Materiales I Preparaduría Tema 3 Prof. Helen Reverón 1.2) Planos a) Dibujar los planos (111) y (020) en un sistema cúbico Los índices planares representan el inverso del punto de corte con la celda unitaria. El plano (111) corta al eje X en 1/1=1; al eje Y en 1/1=1; al eje Z en 1/(1)= -1 Una vez dibujado el plano puede ser trasladado al origen De igual forma, el plano (020) corta al eje X en 1/0 = (es decir, no lo corta), al eje Y en ½; al eje Z en 1/0 = (no lo corta) b) Nombrar las intersecciones de los planos (311) y (220) De nuevo, se tienen los índices hkl de los inversos. Los puntos son para: (311) 1/3 en X; 1 en Y; 1 en Z (220) ½ en X; ½ en Y; en Z 4 Ciencia de los Materiales I Preparaduría Tema 3 Prof. Helen Reverón c)Identificar el plano de la figura Si se toman de una vez los inversos de los puntos de corte, tendríamos 1/0 en X; 1/0 en Y; en Z se tienen infinitos puntos de corte. Luego el plano sería ( 0). Pero los planos deben ser escritos con números enteros. Para determinar el plano, éste no debe pasar por el origen del sistema de coordenadas. Sin embargo, se puede hacer una traslación del plano a una celda vecina, o sea: Este plano corta al eje X en –1; al eje Y en 1; al eje Z en . El plano es entonces (1/(-1) 1/1 1/) (110) II. DENSIDADES ATÓMICAS 2.1) Calcular la densidad lineal del litio y del plomo en la dirección [111] 5 Ciencia de los Materiales I Preparaduría Tema 3 Prof. Helen Reverón El litio tiene estructura bcc. En sistemas cúbicos la densidad atómica lineal es el inverso de la distancia interatómica de repetición “r”, que en este caso, es igual a dos radios atómicos (entre el origen y el átomo central) en la dirección [111] = 1/ (2rLi) = 1/ (2 x 0,152 nm) =3,28 nm-1 Por otra parte, el plomo es fcc. En esta dirección se interceptan los átomos en los vértices a una distancia 3a , siendo “a” el parámetro reticular que, en fcc, está determinado por la diagonal de las caras como se muestra en la figura de abajo. De aquí, rPb 2rPb rPb 2a 4rPb 2a 4 a 0,495nm 2rPb Donde rpb es el radio atómico del plomo (0,175 nm). Entonces la distancia de 3a 0.857nm r repetición es luego 1 1 1,166nm1 r 0,857 6 Ciencia de los Materiales I Preparaduría Tema 3 Prof. Helen Reverón 2.2) Calcular la densidad planar del aluminio en (110) El plano tiene un área de A a x 2a 2a 2 donde 2a 4rAl 4(0,143) 0,572nm así a 0,404nm A 2 (0,404) 2 0,231nm2 Por otra parte el plano pasa por 4 átomos en las esquinas (ocupando la cuarta parte de cada uno) y dos átomos en la mitad de las dos caras (ocupando la mitad de cada uno). La densidad planar es 1 1 x4 x2 at 2 4 8,658 0,231 nm 2 III. DENSIDAD DE MATERIALES 3.1) Calcular la densidad del cloruro de sodio y comparar con su valor experimental (2,16 gr/cm3) Por definición, m , se depende de cuán compacto sea el arreglo de la V celda unitaria del NaCl. Se tiene que la masa depende del número de átomos tal que m n M Na M Cl donde N *n es el número de átomos por celda unitaria *M es el peso atómico *N es el número de Avogadro 1 1 át Luego, n 8 6 4 8 tanto al sodio como al cloro, serían 8 en total 2 celda Corresponde 7 Ciencia de los Materiales I Preparaduría Tema 3 Prof. Helen Reverón El volumen es a3, pero el parámetro reticular viene dado por la longitud de las aristas del cubo a 2rNa 2rCl 2(0,102) 2(0,181) 0,566nm a 0,566x10 7 cm át gr gr 4 35,45 22,9 gr ol m ol La densidad es finalmente celda 7 m 2,14 3 3 cm 0,566x10 cm 23 át 6,023x10 celda m ol Por tanto se tiene una buena aproximación al valor experimental IV. TRANSFORMACIONES ALOTRÓPICAS 4.1) Determinar el cambio relativo de volumen cuando se produce la transformación alotrópica de -Fe a -Fe El hierro pasa de estructura bcc a estructura fcc. El Volumen en bcc es Vo a 3 3a 4rFe 4(0,124) 0,496nm a 0,286nm Vo 2,348x10 2 nm3 Pero debe considerarse que en una estructura bcc se tienen dos átomos por celda y en estructura fcc se tienen 4 átomos por celda. Así se requieren dos celdas bcc para convertirse a una celda fcc Entonces el volumen inicial es Vo´ 2Vo 4,696x102 nm3 El volumen final es el de una celda fcc tal que Vf a fcc 3 2a 4rFe 4(0,124) 0,496nm a´ 0,350nm Vf 4,314x10 2 nm3 El cambio relativo en volumen es V 4,314x102 4,696x102 x100 x100 8,13% V 4,696x10 2