exámenes cdm - teoria de maquinas
Anuncio
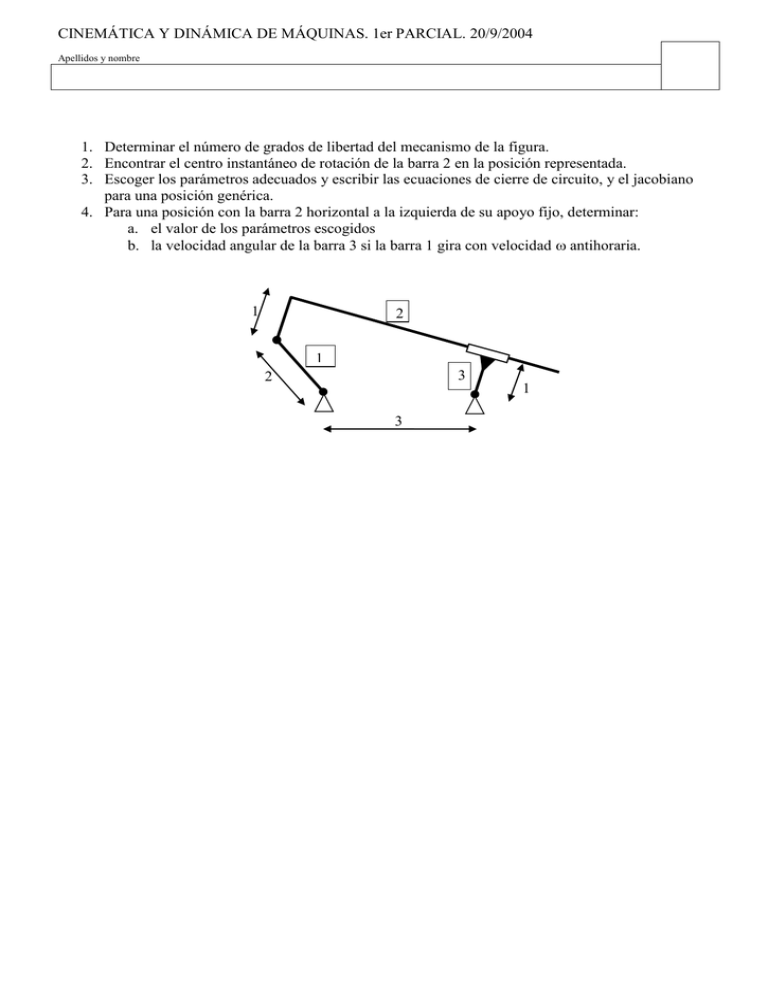
CINEMÁTICA Y DINÁMICA DE MÁQUINAS. 1er PARCIAL. 20/9/2004 Apellidos y nombre 1. Determinar el número de grados de libertad del mecanismo de la figura. 2. Encontrar el centro instantáneo de rotación de la barra 2 en la posición representada. 3. Escoger los parámetros adecuados y escribir las ecuaciones de cierre de circuito, y el jacobiano para una posición genérica. 4. Para una posición con la barra 2 horizontal a la izquierda de su apoyo fijo, determinar: a. el valor de los parámetros escogidos b. la velocidad angular de la barra 3 si la barra 1 gira con velocidad antihoraria. 1 2 1 3 2 1 3 Cinemática y Dinámica de Máquinas. Primer parcial. 12/09/03. apellidos y nombre calificación Demostrar la siguiente afirmación. La posición de un mecanismo de m grados de libertad se define mediante n coordenadas generalizadas x1, x2, … , xn (ángulos o distancias). Se enuncian n-m ecuaciones de cierre de circuito para el mecanismo: L1 x1 , x 2 , x3 , , x n , 0 L2 x1 , x 2 , x3 , , x n , 0 Ln m x1 , x 2 , x3 ,, x n , 0 Si se considera que x1,…,xm es el vector formado por las coordenadas independientes, las demás coordenadas pueden obtenerse como: xm1 , , xn J d 1 x1 ,, xm J i Donde Ji es la matriz formada por las columnas del jacobiano del sistema de ecuaciones correspondientes a las coordenadas independientes, y Jd la matriz formada por las columnas correspondientes a las coordenadas dependientes. Aplicar el resultado al siguiente mecanismo. Determinar antes el número de grados de libertad. Escoger como coordenadas independientes las lineales antes que las angulares. CINEMÁTICA Y DINÁMICA DE MÁQUINAS. 1er PARCIAL. 7/6/2004 Apellidos y nombre 1. Deducir la expresión para el ángulo de presión en una leva con seguidor alternativo de rodillo. Explicar todos los pasos de la deducción. 2. Un seguidor debe partir de velocidad y aceleración nulas y realizar una elevación de valor 1 en 180º, y retornar los 180º restantes. Se requiere continuidad en la aceleración 1. Obtener el polinomio de grado mínimo que cumple las condiciones requeridas. 2. Representar los diagramas de desplazamiento, velocidad y aceleración 3. Trazar la curva de paso y el perfil de leva para un rodillo de diámetro 0,4, un circulo primario de radio 2 y excentricidad 0,6. Nota: realizar los cálculos para el intervalo de 0º a 180º; el intervalo de 180º a 360º es el mismo invertido. Los diagramas y curvas trazarlos entre 0º y 360º. Cinemática y Dinámica de Máquinas. Primer parcial. 30/06/03. apellidos y nombre calificación Se quiere construir un sistema leva-seguidor radial en el que el seguidor de cuña tenga el mismo movimiento que el pistón de un mecanismo biela manivela. El ángulo de presión debe ser siempre menor de 20º. 1. Rango de posibles valores para el radio del círculo primario de la leva. Explicar los criterios utilizados. (definir socavación, discutir si se puede producir en este caso, definir ángulo de presión y la influencia del radio del círculo primario en el ángulo de presión) 2. Diagrama de desplazamientos, velocidades y aceleraciones del seguidor: función matemática y diagrama gráfico aproximado. 3. Trazar el perfil de leva para un círculo primario de radio el doble que la manivela, determinando puntos cada 30º. 4. Determinar la máxima velocidad de la leva sin que se pierda el contacto. Datos: Longitud de la manivela: 1; longitud de la biela: 5 Cinemática y Dinámica de Máquinas. 12/02/04. apellidos y nombre calificación 1. Trazar el esquema cinemática del mecanismo de la figura. (1 pto) 2. Determinar de forma razonada el número de grados de libertad. (1 pto) 3. Escoger las coordenadas adecuadas y escribir las ecuaciones del sistema; hallar el jacobiano para una posición genérica (3 ptos) 4. Determinar, en la posición de la figura, los centros instantáneos de rotación de todas las piezas. (3ptos) 5. Determinar gráficamente, para la posición de la figura, la fuerza necesaria en B para soportar un peso P en el punto A. (utilizar los centros instantáneos de rotación si es necesario) (2 ptos) Cinemática y Dinámica de Máquinas. EXAMEN DE DICIEMBRE. Primer parcial. 13/02/03. apellidos y nombre calificación 5. 6. 7. 8. 9. Realizar el esquema cinemático del mecanismo representado. Determinar y razonar el número de grados de libertad del sistema. Encontrar los centros instantáneos de rotación de todas las piezas. Escribir las ecuaciones de cierre de circuito del mecanismo. Determinar el par en la excéntrica para cualquier ángulo para vencer el peso de la placa cuadrada, supuesta esta homogénea, y despreciando la masa de las demás piezas. Datos: AB=15; R=30; BC=100; AF=185; L (lado de la placa cuadrada):100; M (masa de la placa):10 kg Notas: A es un punto fijo; B es el centro de la excéntrica; A y F están a la misma altura. E R B A C 45 º 45 D º F Cinemática y Dinámica de Máquinas. Dinamica. 20/12/03. apellidos y nombre calificación Se desea equilibrar un rotor; para ello, se hace girar apoyado como se indica en la figura 1 en un eje horizontal, y se miden las reacciones en los apoyos. De esta medida, se obtienen las gráficas de la figura 2, que representan el valor de las reacciones verticales en los apoyos 1 y 2, medidas con respecto al bastidor fijo. En la figura se indican los planos de equilibrado. Las masas equilibrantes deben colocarse a una distancia de 200 mm del eje. P.E. 1 1. Determinar el valor de las reacciones estáticas en los apoyos y el peso del rotor. 2. Determinar la velocidad angular a la que se realizó la medida. 3. Representar las reacciones dinámicas en un sistema de referencia solidario al rotor. 4. Determinar el valor y la posición de las masas equilibrantes. P.E. 2 Apoyo 2 Apoyo 1 150 150 800 1100 Kg fuerza 180 170 160 150 140 130 120 110 100 90 80 70 60 50 40 apoyo 1 30 apoyo2 20 10 0 0 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,1 0,11 0,12 0,13 0,14 Segund os

