EJERCICIOS DE TRABAJO Y ENERGÍA RESUELTOS:

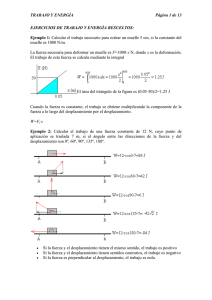
TRABAJO Y ENERGÍA
Página 1 de 2
EJERCICIOS DE TRABAJO Y ENERGÍA:
Ejemplo 1: Calcular el trabajo necesario para estirar un muelle 5 cm, si la constante del
muelle es 1000 N/m.
Ejemplo 2: Calcular el trabajo de una fuerza constante de 12 N, cuyo punto de
aplicación se traslada 7 m, si el ángulo entre las direcciones de la fuerza y del
desplazamiento son 0º, 60º, 90º, 135º, 180º.
Ejemplo 3: Hallar la velocidad con la que sale una bala después de atravesar una tabla
de 7 cm de espesor y que opone una resistencia constante de F=1800 N. La velocidad
inicial de la bala es de 450 m/s y su masa es de 15 g.
Ejemplo 4:
Sobre una partícula actúa la fuerza F=2xyi+x2j N
Calcular el trabajo efectuado por la fuerza a lo largo del
camino cerrado ABCA.



La curva AB es el tramo de parábola y=x2/3.
BC es el segmento de la recta que pasa por los puntos
(0,1) y (3,3) y
CA es la porción del eje Y que va desde el origen al
punto (0,1)
Ejemplo 5:
Un cuerpo de 2 kg se deja caer desde una altura de 3 m. Calcular
1. La velocidad del cuerpo cuando está a 1 m de altura y cuando
llega al suelo, aplicando las fórmulas del M.R.U.A.
2. La energía cinética potencial y total en dichas posiciones
Tomar g=10 m/s2
Ejemplo 6: Un bloque de masa 0.2 kg inicia su movimiento hacia arriba, sobre un plano
de 30º de inclinación, con una velocidad inicial de 12 m/s. Si el coeficiente de
rozamiento entre el bloque y el plano es 0.16. Determinar:


la longitud x que recorre el bloque a lo largo del plano hasta que se para
la velocidad v que tendrá el bloque al regresar a la base del plano
TRABAJO Y ENERGÍA
Página 2 de 2
Ejemplo 7: Una partícula de masa m desliza sobre una superficie en forma de cuarto de
circunferencia de radio R, tal como se muestra en la figura. Datos R = 2m, m = 2kg y
velocidad final V = 4m/s. Determinar el trabajo que hace la fuerza de rozamiento en
este recorrido.
Ejemplo 8: Una partícula se encuentra inicialmente en reposo sobre el vértice de la
cúpula, en una posición de equilibrio inestable. Cuando se desvía ligeramente de esta
posición, la partícula desliza sin rozamiento, incrementando su velocidad hasta que
llega un momento en el que deja de tener contacto con la cúpula. Calcular la posición θc
para la que abandona la cúpula. Indicar una vez está en el aire el punto del suelo dónde
impacta. Radio de la cúpula R=15 m
Ejemplo 9: A un muelle de k=1000 N/m, que está en vertical, se le engancha una m=10
kg. Determina la posición de equilibrio xo y el período de las oscilaciones. Si desde este
equilibrio se estira hacia abajo una distancia a xo determina cuál es la ecuación del
movimiento.
Ejemplo 10: Un bloque parte de la posición x0 sobre un plano inclinado con velocidad
inicial nula. Teniendo en cuenta los siguientes datos: Coeficiente de rozamiento μ=0.3,
Masa del bloque, m=1 kg, Angulo del plano inclinado θ=30º, Constante elástica del
muelle, k=50 N/m, Posición inicial del bloque x0 =-1.0 m. Determinar en primer lugar
que efectivamente se mueve y después: tiempo que tarda en impactar con el resorte,
velocidad con la que impacta, deformación máxima que le produce al resorte, velocidad
del bloque al volver a pasar por el origen subiendo, altura a la que llega,….
Ejemplo 11: Un bloque parte de la posición x0 sobre un plano inclinado con velocidad
inicial nula. Teniendo en cuenta los siguientes datos: Coeficiente de rozamiento μ=0.24,
Masa del bloque, m=1 kg, Angulo del plano inclinado θ=40º, Constante elástica del
muelle, k=50 N/m, Posición inicial del bloque x0 =-1.0 m. Determinar en primer lugar
que efectivamente se mueve y después: tiempo que tarda en impactar con el resorte,
velocidad con la que impacta, deformación máxima que le produce al resorte, velocidad
del bloque al volver a pasar por el origen subiendo, altura a la que llega,…. Solución: V
= 3m/s, xmáx = 52,4cm V = -2,29m/s , x que recorre hacia arriba hasta que se detiene x =
-32cm.