tomo 2.2
Anuncio
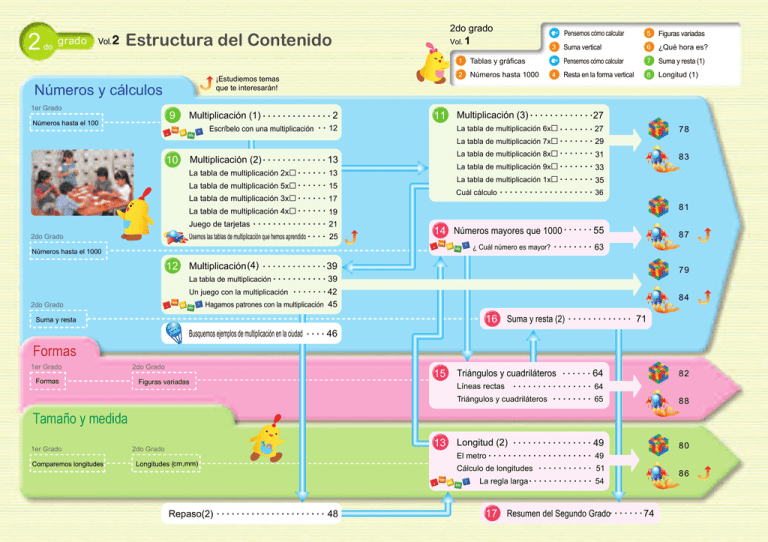
2 grado do Vol. 2 2do grado Estructura del Contenido ¡Estudiemos temas que te interesarán! Números y cálculos 1er Grado 9 Números hasta el 100 Vol. 1 10 Multiplicación (1) . . . . . . . . . . . . . . 2 Escríbelo con una multiplicación . . 12 11 3 1 TDEODV\JUi¿FDV 2 Números hasta 1000 4 Pensemos cómo calcular 5 Figuras variadas Suma vertical 6 ¿Qué hora es? Pensemos cómo calcular 7 Suma y resta (1) Resta en la forma vertical 8 Longitud (1) Multiplicación (3) . . . . . . . . . . . . . 27 La tabla 12 de multiplicación 6xƑ ・・・ . . . . . . . 27 La tabla de multiplicación 7xƑ . . . . . . . 29 La tabla de multiplicación 8xƑ . . . . . . . 31 La tabla de multiplicación 9xƑ . . . . . . . 33 La tabla de multiplicación 1xƑ . . . . . . . 35 Cuál cálculo . . . . . . . . . . . . . . . . . . . 36 Multiplicación (2) . . . . . . . . . . . . . 13 La tabla de multiplicación 2xƑ . . . . . . 13 La tabla de multiplicación 5xƑ . . . . . . 15 La tabla de multiplicación 3xƑ . . . . . . 17 Usemos las tablas de multiplicación que hemos aprendido . . . . 25 2do Grado 14 Números mayores que 1000 . . . . . . 55 Multiplicación (4) . . . . . . . . . . . . . 39 79 La tabla de multiplicación . . . . . . . . . . . 39 Un juego con la multiplicación . . . . . . . 42 84 Hagamos patrones con la multiplicación 45 2do Grado 87 ¿ Cuál número es mayor? . . . . . . . . 63 Números hasta el 1000 12 83 81 La tabla de multiplicación 4xƑ . . . . . . 19 Juego de tarjetas . . . . . . . . . . . . . . . 21 78 16 Suma y resta (2) . . . . . . . . . . . . . 71 Suma y resta Busquemos ejemplos de multiplicación en la ciudad . . . . 46 Formas 1er Grado Formas 2do Grado Figuras variadas 15 Triángulos y cuadriláteros . . . . . . 64 82 . . . . . . . . . . . . . . . . 64 Triángulos y cuadriláteros . . . . . . . . 65 88 Longitud (2) . . . . . . . . . . . . . . . . 49 80 Líneas rectas Tamaño y medida 1er Grado Comparemos longitudes 94 13 2do Grado Longitudes (cm,mm) Repaso(2) . . . . . . . . . . . . . . . . . . . . . . 48 El metro . . . . . . . . . . . . . . . . . . . . . 49 Cálculo de longitudes . . . . . . . . . . . 51 La regla larga . . . . . . . . . . . . . 54 17 Resumen del Segundo Grado. . . . . . . 74 86 95 9 1 Multiplicación (1) Disfrutando una fiesta ① ¿Cuántas manzanas hay? ② ¿Cuántas donas hay? ③ ¿Cuál es la diferencia entre el número de manzanas y el número de donas en cada plato? ④ Busca dónde hay el mismo número de cosas en cada plato, como los pastelitos, y expresa el número total. El número total de pastelitos se expresa como " 2 por plato y El número total de donas puede expresarse como "3 por plato y hay 5 platos, en total son 15." 2 Es fácil porque cada plato tiene el mismo número de donas. El número total de " por plato y platos son ." se expresa como platos son ." 3 2 Encuentra el número total donde hay grupos con la misma cantidad. ① 3 cajas con 8 piezas de chocolate. Hay 5 cajas con 2 pasteles, entonces el total es 2 por caja 5 cajas y hacen 10 . Esto se escribe como 25=10 y se lee por caja y cajas hacen "5 veces 2 es 10" o "2 multiplicado por 5 es . igual a 10." ② 6 paquetes con 2 pescados 2 número por caja por paquete y paquetes hacen . ③ 5 bolsas con 6 caramelos 5 = número de cajas 10 número total Este tipo de cálculo se llama "multiplicación". 3 ¿Cuántas galletas hay? por bolsa y bolsas hacen . ④ 2 platos con 9 peras Número por bolsa = Número de bolsas Número total La multiplicación es la operación que se usa para obtener el total cuando tienes el mismo número de por plato y 4 platos hacen . objetos por grupo y conoces el número de grupos. 5 4 Escribe una multiplicación cuando encuentres algo que tenga el mismo número por grupo. man zan as 6 = = = = = = = ¿Hay otro ejemplo? 7 5 ¿Cuántos hay? Comprueba usando los bloques y haz una 7 Pon el mismo número de limones en varias bolsas. ¿De cuántas maneras puedes ponerlos en las bolsas? multiplicación. Representa estas maneras usando multiplicaciones. ① Pelotas ① Cuando hay 12 limones. = Si hay 3 en cada bolsa, ¿qué sucede? Si pongo 2 en cada bolsa, obtengo 6 bolsas. ② Fresas Aún hay otras formas, ¿no es así? ② Cuando hay 24 limones. = 6 Usa los bloques para representar las siguientes multiplicaciones. ① 3 7 ② 5 2 ③ 8 4 ④ 2 5 8 Si hay 4 en cada bolsa… Como el número es mayor, tenemos más posibilidades. 9 2B cm 8 Hay algunos pedazos de cinta. ¿Cuántos cm de largo tiene 1 pedazo de cinta, 2 pedazos, 3 pedazos? 1 Expresa estos problemas usando 1 grupo 21 = 2 grupos 2 = 3 grupos 2 = 2 multiplicaciones. ① ¿Cuántos pescados hay? pescados por paquete y . paquetes hacen Multiplicación: 1 grupo, 2 grupos y 3 Midamos usando una regla. grupos también se puede decir: = ② ¿Cuántas mandarinas hay en total? 1 vez, 2 veces y 3 veces. Multiplicación: 9 Hay el mismo número de latas en cada caja. . bolsas hacen por bolsa y = ③ ¿Cuántos cm de largo mide la cinta? 2B cm 2B cm 2B cm 2B cm cm por trozo de cinta y Número por caja Multiplicación: = Número de cajas Número total de latas ① Escribe una multiplicación para obtener el total de latas. ② ¿Cuántas veces 8 es el número total de latas? ③ ¿Cuántas latas hay? La respuesta de 8 6 es igual a la respuesta de 8 + 8 + 8 + 8 + 8 + 8 . 10 Es más difícil sumar 6 veces el 8. 2 2B cm trozos hacen 2B cm . = Hay 6 barras de chocolate en cada caja. ① Escribe una multiplicación para obtener el número total de barras. ② ¿Cuántas veces 6 es el total? ③ ¿Cuántas barras de chocolate hay en total? Ir a página 12 11 Escríbelo con una multiplicación ● Escribe el número de ★ con una multiplicación. ① Si muevo así, 10 Multiplicación (2) Construyamos una tabla de multiplicar. La tabla de multiplicación 2 × ☐ ② 1 2 niños van en cada bote. ① Encontremos el número total de niños cuando el número la multiplicación es 3 . de botes aumenta de 1 a 5. 21= Si pienso en como un grupo, la multiplicación es 2 . ● 22= 23= Encierra algunas ★ para obtener 34. 24= ② Encontremos el número total de niños cuando el número de botes aumenta de 6 a 9. La idea de Takeshi ▼ La idea de Eiko ▼ ¿Cuántas otras formas puedes encontrar? número de niños por bote 25= 26= 27= 28= 29= 5 botes 2 9 = 1 8 se lee "2 multiplicado por 9 es igual a 18" 12 13 2 Haz tarjetas de La tabla de multiplicación de 2 x☐ multiplicación de 2 ☐ y 21=2 … dos por uno es 2 úsalas para practicar. frente La tabla de multiplicación de 5 ×☐ dos cuatro 22=4 … dos por dos es 4 1 Hay 5 galletas en cada plato. seis 23=6 … dos por tres es 6 atrás ocho 24=8 … dos por cuatro es 8 diez 25=10 … dos por cinco es 10 doce 26=12 … dos por seis es 12 3 Haz dibujos para 2 ☐. ① Encuentra el número total de galletas cuando el número de platos aumenta de 1 a 5. catorce 27=14 … dos por siete es 14 51= dieciseis 28=16 … dos por ocho es 16 52= dieciocho 29=18 … dos por nuevo es 18 53= Decide cuál es la expresión que corresponde. 54= 55= 4 Escribe una multiplicación para estas imágenes. ① ② Encuentra el número total de galletas ② cuando el número total de platos 56= aumenta de 6 a 9. 57= 58= 5 Inventa un problema que 59= se resuelva con 27. Cada niño hace cisnes de origami. ¿Cuántos cisnes pueden hacer 14 niños? Desliza una hoja de papel sobre las columnas para mostrarlas una a una. 15 2 Haz tarjetas de La tabla de multiplicación de 5 x ☐ multiplicación de 5 ☐ y 1 Hay 3 porciones de jalea cinco 51=5 … cinco por uno es 5 diez 52=10 … cinco por dos es 10 úsalas para practicar. en cada plato. quince 53=15 … cinco por tres es 15 veinte 54=20 … cinco por cuatro es 20 veinticinco 55=25 … cinco por cinco es 25 3 La tabla de multiplicación de 3☐ ① Encontremos el número total de gelatinas cuando el número de platos aumenta de 1 a 4. treinta 56=30 … cinco por seis es 30 Haz dibujos para 31= treinta y cinco 57=35 … cinco por siete es 5 ☐. 35 cuarenta 58=40 … cinco por ocho es 32= 40 cuarenta y cinco 59=45 … cinco por nueve es 45 33= 34= 4 Inventa un problema que se resuelva con la tabla de multiplicar 5 ☐. 5 cm de cinta 5 pastelitos en cada caja ② Encuentra el número total de 35= gelatinas cuando el número de 36= platos aumenta de 5 a 9. ¿Cuántos cm de listón se forman con listones? 37= 38= 39= 5 Multiplica el número del centro por los números que están ③ Si se agrega un plato más, ¿cuántas gelatinas habrá? alrededor del círculo y escribe tus respuestas en el espacio correcto. 16 17 2 Haz tarjetas y dibujos La tabla de multiplicación de 3 x ☐ de la multiplicación 31=3 … tres por uno es 3 3 ☐. 32=6 … tres por dos es 6 La tabla de multiplicación de 4☐ 1 Construimos unos tres seis carritos. Pusimos 4 llantas nueve 33=9 … tres por tres es 9 doce 34=12 … tres por cuatro es 12 quince 35=15 … tres por cinco es 15 dieciocho 36=18 … tres por seis es 18 en cada uno. ① Encuentra el número total de llantas cuando el número de carritos se incrementa de 1 a 4. veintiuno 37=21 … tres por siete es 21 41= veinticuatro 38=24 … tres por ocho es 24 veintisiete 42= 39=27 … tres por nueve es 27 3 ¿Cuántas hay? Responde usando una multiplicación. ① Barras de jabón ② Manjus (un tipo de pastel japonés) 43= Tres de cuatro son doce. Hay 12 barras de jabón. 44= ② Calculemos el número total de llantas cuando el número de carritos se ③ Calcomanías 45= 46= incrementa de 5 a 9. 47= 48= 49= 4 Hay 3 pepinos en cada bolsa. ¿Cuántos pepinos habrá en 6 bolsas? ③ Cuando el multiplicador Multiplicando 6 se incrementa en 1 (de 4 46 a 47), ¿cuánto aumenta el producto? 18 Multiplicador 6 incrementa en 1 4 producto = 24incrementa en 7 = 19 2 Haz tarjetas de La tabla de multiplicación de 4 x☐ multiplicación de 4 ☐ y 41=4 … cuatro por uno es 4 cuatro úsalas para practicar. Juego de tarjetas Escribe multiplicaciones en unas tarjetas ocho 42=8 … cuatro por dos es 8 y en otras las respuestas para 2☐, 3☐, doce 43=12 … cuatro por tres es 12 dieciseis 44=16 … cuatro por cuatro es 16 4☐ y 5☐. Luego juega con ellas. veinte 45=20 … cuatro por cinco es 20 46=24 … cuatro por seis es veinticuatro 24 ① Elige una respuesta. veintiocho 47=28 … cuatro por siete es 28 48=32 … cuatro por ocho es treinta y dos 32 treinta y seis 49=36 … cuatro por nueve es 36 3 Juntemos 3 cintas que miden 4 cm de largo cada una. ¿Cuántos cm de cinta obtendremos? ② Encuentra la multiplicación que corresponde a la respuesta que elegiste. (1). 4 Multiplica el número del centro por los números que están alrededor del círculo y escribe tus respuestas en el espacio correcto. 20 21 ③ ¿Cuál es mayor? 1 ¿Cuál es mayor, o ¿Cuál es mayor, 5 ? 6 o 3 9 ? ¿Qué pasa cuando las respuestas son iguales? ④ Elige dos tarjetas: una multiplicación y su respuesta. Haz estas multiplicaciones. páginas13-20 ① 22 ② 53 ③ 37 ④ 36 ⑤ 28 ⑥ 57 ⑦ 59 ⑧ 41 ⑨ 32 ⑩ 33 ⑪ 46 ⑫ 27 ⑬ 48 ⑭ 39 ⑮ 45 ⑯ 29 ⑰ 52 ⑱ 44 ⑲ 54 ⑳ 25 21 56 42 24 21 22 2 38 23 2 niños pasean en cada auto chocador. Hay 4 autos. ¿Cuántos niños hay? página 13 3 Hay 3 berenjenas en cada bolsa. ¿Cuántas berenjenas hay en 6 bolsas? Si tomas el y , ¿puedes compararlas? página 17 22 23 Usemos las tablas de multiplicación que hemos aprendido 4 Escribe abajo lo que has aprendido acerca páginas 13-20 de la tabla de multiplicar. Multiplicador Multiplicando renglón del 2 2 renglón del 3 3 renglón del 4 4 renglón del 5 5 1 2 3 4 5 6 7 8 9 1 ¿Cuántas estampillas hay? Piensa cómo puedes usar las tablas de multiplicar que aprendiste. 4 15 28 15 ① Cambia el orden de los números en los renglones y construye otra tabla de multiplicar. Multiplicando Multiplicador renglón del 3 3 renglón del 4 4 renglón del 2 2 renglón del 5 5 1 2 3 4 5 6 7 8 9 ② Cambia el orden de los números en los renglones y construye otra tabla de multiplicar. Multiplicador Multiplicando 1 2 3 4 5 6 7 8 9 Es una buena idea separar las estampillas. 24 No hemos aprendido 7 □, así que, … 25 11 La idea de Natsumi ▼ Separa la hoja cerca del centro. Multiplicación (3) La tabla de multiplicación de 6☐ 1 Hay 6 piezas de queso en cada caja. ¿Cuántas piezas de queso hay en 3 cajas? ① Escribe una multiplicación. Sumamos la respuesta de 36 y la respuesta de 46 y obtenemos . 6 en cada caja y hay 3 cajas, da … ② Obtén la respuesta. 2 Haz la tabla de multiplicar para 6 ☐. La idea de Ryoichi ▼ 61= 62= 63= ① Escribe las respuestas. Sumamos la respuesta de 26 y la respuesta de 56 y obtenemos . ② Cuando el multiplicador se incrementa en 1, ¿cuánto se incrementa la respuesta? La idea de Yasuo ▼ Multiplicando Mira de lado el libro de texto y separa la hoja justo en el centro. Multiplicador Producto 6 2 = 12 6 3 = 64= 65= 66= 67= 68= 69= Si el multiplicador se incrementa en 1, Es 2 veces la respuesta de 37, por lo tanto son 26 . la respuesta se incrementa en el valor del multiplicando. 27 La tabla de multiplicación de 7☐ 3 Haz tarjetas y dibujos de La tabla de multiplicación de 6 x ☐ la tabla de multiplicación 61=6 … seis por uno es 6 seis 6 ☐. doce 1 Hay 7 plumones en cada caja. ¿Cuántos plumones hay 62=12 … seis por dos es12 dieciocho 63=18 … seis por tres es 18 veinticuatro 64=24 … seis por cuatro es 24 treinta 65=30 … seis por cinco es 30 66=36 … seis por seis es treinta y seis 67=42 … seis por siete es 36 cuarenta y dos 42 cuarenta y ocho 68=48 … seis por ocho es 48 cincuenta y cuatro 69=54 … seis por nueve es 54 en 4 cajas? ① Escribe una multiplicación. ② Obtén la respuesta. 2 Haz una tabla de multiplicación para 7 ☐. Usa lo que aprendiste sobre la tabla de multiplicación y cuánto se incrementa la respuesta cuando el multiplicador 4 Calcula estas cantidades usando multiplicaciones. aumenta en 1. ① El número total de pececitos ② El número total de donas. 71= 72= 73= Para 7 ☐,la respuesta se incrementa en ……. 74= 75= 76= 5 Inventa un problema que se resuelva con la tabla 77= de multiplicar 6 ☐. 78= La respuesta para 72 es la misma que la de 27. La respuesta para 73 es la misma que la de 37. Así que podemos construir la tabla hasta 76. 28 79= 29 3 Haz tarjetas y dibujos de La tabla de multiplicación de 7 x ☐ 1 Cada niño recibe un siete la tabla de multiplicación 71=7 … siete por uno es 7 7 ☐ . 72=14 … siete por dos es 14 catorce veintiuno 73=21 … siete por tres es 21 veintiocho 74=28 … siete por cuatro es 28 75=35 … siete por cinco es 76=42 … siete por seis es La tabla de multiplicación de 8 x☐ treinta y cinco 35 listón de 8 cm. ¿Cuántos cm de listón se necesitan para 3 niños? cuarenta y dos 42 cuarenta y nueve 77=49 … siete por siete es 78=56 … siete por ocho es Hay 7 días en la semana. ¿Cuántos días hay en 3 semanas? 8cm 8cm para uno para uno para uno 49 cincuenta y seis 79=63 … siete por nueve es 4 8cm 56 sesenta y tres 63 ① Escribe una multiplicación. ② Obtén la respuesta. 2 Haz una tabla de multiplicación para 81= 8 ☐ usando lo que has aprendido y las 8 2 = reglas de la multiplicación. 83= 84= 5 85= Multiplica el número del 86= centro por los números que están alrededor del círculo y escribe las respuestas en el espacio correcto. 30 Cuando el multiplicador se incrementa en 1, la respuesta … La respuesta a 83 es igual a la respuesta de 38, ¿verdad? 87= 88= 89= 31 3 Haz tarjetas y dibujos de la tabla de multiplicación para 8 ☐. La tabla de multiplicación de 8 x ☐ ocho 81=8 … ocho por uno es 8 dieciseis 82=16 … ocho por dos es 16 83=24 … ocho por tres es veinticuatro 24 84=32 … ocho por cuatro es La tabla de multiplicación de 9☐ treinta y dos 32 cuarenta 85=10 … ocho por cinco es 40 86=48 … ocho por seis es 87=56 … ocho por siete es cuarenta y ocho 48 cincuenta y seis 88=64 … ocho por ocho es 56 sesenta y cuatro 64 1 Un equipo de béisbol tiene 9 jugadores. ¿Cuántos jugadores hay en 4 equipos? ① Escribe una multiplicación. ② Obtén la respuesta. 4 Cada niño recibe 8 hojas de papel de color, ¿cuántas hojas se necesitan para 6 niños? 2 Haz una tabla de multiplicación 91= para 9 ☐. Usa lo que has aprendido 9 2 = y las reglas de la multiplicación. 93= 94= 95= 5 Multiplica el número del 96= centro por los números que 97= están alrededor del círculo y escribe tus respuestas en el espacio correcto. 32 Podemos obtener las respuestas de lo que hemos aprendido, excepto 91 y 99. Cuando el multiplicador se incrementa en 1, la respuesta … 98= 99= 33 3 Hagamos tarjetas y dibujos de la tabla de multiplicación para 9 □. La tabla de multiplicación de 1□ La tabla de multiplicación de 9 x □ nueve 91=9 … nueve veces uno es 9 dieciocho 92=18 … nueve veces dos es 18 veintisiete 93=27 … nueve veces tres es 27 trenita y seis 94=36 … nueve veces cuatro es 36 95=45 … nueve veces cinco es 96=54 … nueve veces seis es cuarenta y cinco 45 1 Una familia hizo una fiesta de cumpleaños. Prepararon 3 caramelos, 2 naranjas y un pastel para cada persona. ¿Cuántas de estas cosas necesitaron si cincuenta y cuatro 54 sesenta y tres 97=63 … nueve veces siete es 63 asistieron a la fiesta 4 personas? setenta y dos 98=72 … nueve veces ocho es 72 ochenta y uno 99=81 … nueve veces nueve es 81 Caramelos 3 4 = Naranjas 2 4 = = Pastel 4 Inventa un problema de multiplicación que esté relacionado con la imagen de abajo. 2 Hagamos una tabla de multiplicación para 1 □. 3 Hagamos tarjetas y dibujos de la tabla de multiplicación para 1 □. El secreto de 9 x □ ● Dile a todos lo que observas en la tabla de multiplicación para 9×□. 34 ¿Cómo son los números de las respuestas de 9□? 9 18 27 36 45 54 63 72 81 Si sumamos el número que está en el lugar de las unidades y el número que está en las decenas, las respuestas siempre son … La tabla de multiplicación de 1 x □ 1 1 = 1 … una vez uno es 1 2 = 2 … una vez dos es 1 3 = 3… una vez tres es uno 1 dos 2 tres 3 cuatro 1 4 = 4 … una vez cuatro es 4 1 5 = 5 … una vez cinco es 1 6 = 6 … una vez seis es 1 7 = 7 … una vez siete es cinco 5 seis 6 siete 7 ocho 1 8 = 8 … una vez ocho es 8 1 9 = 9 … una vez nueve es nueve 9 35 Cuál cálculo 1 1 Hay 8 fresas en cada plato. Hay 3 platos. ¿Cuántas fresas hay? ¿Qué es lo que nosotros deseamos saber? páginas 27-35 ① 62 ② 83 ③ 71 ④ 12 ⑤ 67 ⑥ 94 ⑦ 87 ⑧ 99 ⑨ 85 ⑩ 15 ⑪ 73 ⑫ 68 ⑬ 65 ⑭ 18 ⑮ 96 ⑯ 95 ⑰ 98 ⑱ 79 ⑲ 93 ⑳ 14 ㉑ 91 ㉒ ㉓ ㉔ 81 2 ¿Qué es lo que nosotros sabemos? Hagamos multiplicaciones. 77 63 Hay 6 donas en cada caja. Hay 4 cajas. ¿Cuántas donas hay en total? página 27 2 Hay 9 donas en la caja. Si te comes 7, ¿cuántas quedan? 3 Hay 9 naranjas en el canasto y 4 naranjas en el plato. ¿Cuántas naranjas hay en total? 4 Se dieron lápices a 7 niños. Cada niño recibió 3 lápices. ¿Cuántos lápices se dieron en total? 36 3 Cada niño recibe 7 fichas. ¿Cuántas fichas se necesitan para 8 niños? página 29 37 12 1 Multiplicación (4) Hagamos multiplicaciones. ① 6×6 ② 1×3 ③ 8×4 ④ 9×2 ⑤ 7×5 ⑥ 6×1 ⑦ 1×7 ⑧ 6×9 ⑨ 8×9 ⑩ 8×6 ⑪ 9×7 ⑫ 7×8 2 Compramos 8 bolsas de naranjas. Había 5 naranjas en cada bolsa. La tabla de multiplicación 1 Hagamos una tabla de multiplicación y busquemos sus secretos. ① Hagamos una tabla de multiplicación. multiplicador multiplicando fila del 1 ¿Cuántas naranjas había en total? ① Haz un dibujo. ② Escribe una expresión matemática y obtén la respuesta. fila del 2 fila del 3 fila del 4 3 Cuenta la cantidad de usando la multiplicación. ① ② fila del 5 fila del 6 fila del 7 fila del 8 fila del 9 4 " 16 es la respuesta para 2 en la fila del 8. 82=16 Haz un problema para 73 usando las ② palabras “galleta” y “plato". ■ Ir a la página 78 38 Ir a la página 83 Colorea la tabla en la página 92. Busca los secretos en la tabla de multiplicación. ¿Cómo se incrementan las respuestas? ¿Dónde están las mismas respuestas? ¿Cómo están alineados los números? 39 ③ Di lo que has descubierto sobre la tabla de 2 Comparemos las respuestas cuando el multiplicando es 3 y cuando el multiplicador es 3. multiplicación. El descubrimiento de Yoko ▼ En la fila del 5, en el lugar de las unidades está 0 o 5, y así sucesivamente. ① Comparemos la respuesta de 35 y la respuesta de 53. 5, 10, 15, 20, 25 El descubrimiento de Yoshio ▼ Las mismas respuestas están junto a la diagonal, opuestas una contra otra. ② ¿Qué es lo que observas? El descubrimiento de Yasuo ▼ Hay respuestas que aparecen más de una vez. En la multiplicación la respuesta es la El 2 aparece 2 veces, el 4 aparece 3 veces, y el 6 misma si intercambiamos el multiplicando aparece 4 veces. y el multiplicador. Hay muchos secretos, ¿verdad? Pareciera que aún hay más secretos. 3 Escribe los números que faltan en el ① 3×8= ③ En esta tabla de multiplicación, el número de monedas coincide con la respuesta para cada multiplicación. ×5=5×6 ② 4× =7×4 ④ 9×2=2× Encontremos todas las expresiones multiplicativas para las siguientes respuestas. ① 40 ×3 . 9 ② 12 ③ 36 ④ 54 41 Un juego con la multiplicación 1 2 Realiza el juego de la multiplicación ① de la página Haz el juego de la multiplicación ② de la página 90 para que recuerdes mejor la tabla de multiplicación. 90 para que recuerdes mejor la tabla de multiplicación ① Escribe las respuestas en los espacios de la tabla de abajo. ① Elabora un plan para ganar el juego. No deberías escribir 25 porque sólo aparece una vez en la tabla. columna fila Deberías escribir 12 porque aparece 4 veces en la tabla. ② Observa la tabla de multiplicación y encuentra las respuestas que sólo aparecen una vez. Un ejemplo es 25 ③ Encuentra las respuestas que aparecen 4 veces. Un ejemplo es 12 ④ Comencemos el juego. ② Comencemos el juego. Haz un dado utilizando una caja vacía. 42 43 1 Las tablas de abajo son una parte de la tabla de multiplicación. ¿ Cuáles son los lugares adecuados para las tablas: aa, y ? Justifica tus respuestas. ② ① ● Traza líneas para unir los números que están en el lugar de las unidades en las respuestas de 3□. Haz lo mismo para las otras multiplicaciones. ③ 12 14 16 18 12 18 24 30 4 6 18 21 24 27 14 21 28 35 6 9 24 28 32 36 16 24 32 40 8 12 16 20 30 35 40 45 18 27 36 45 ④ , Hagamos patrones con la multiplicación 8 10 12 15 Comienza con 0 y termina con 0. 3×1= 3×2= 3×3= 3×4= 3×5= 3×6= 3×7= 3×8= 3×9= 3 6 9 12 15 18 21 24 27 10 15 20 25 multiplicador 36 42 48 54 multiplicando 42 49 56 63 fila del 1 48 56 64 72 fila del 3 54 63 72 81 fila del 4 fila del 2 fila del 5 fila del 6 fila del 7 fila del 8 fila del 9 2 Escribe todas las multiplicaciones cuya respuesta sea 24. ■ Ir a la página 45 44 ■ Ir a la página 79 ■ Ir a la página 84 45 Busquemos ejemplos de multiplicación en la ciudad. Hay muchas cosas con los mismos números en la ciudad. ¿Te refieres a que hay muchas cosas que se pueden contar mediante la multiplicación? Vamos a comprobar. ● Yo encontré 84 para las ventanas de un edificio. Busca con tus amigos algunas cosas 3 lápices en cada paquete. Hay 5 paquetes en un negocio. Encontré 35. que se puedan contar usando la multiplicación. Cada señal de tránsito tiene 3 luces. Yo encontré 56 en un almacén. Multiplicación en la ciudad Es un grupo de Modo que se expresa como 31. ● Di a tus amigos lo que encontraste diseñando un periódico. Hay 5 manzanas en cada canasto así que el total es 56. 3 lápices en cada bolsa, es 35. Si pensamos este grupo de ventanas como un grupo, obtenemos 48. 46 47 G 4 1 R U C 13 Q 10 11 Hagamos multiplicaciones. ① 2×4 ② 5×1 ③ 3×7 ④ 2×3 ⑤ 6×9 ⑥ 8×2 ⑦ 7×6 ⑧ 6×4 ⑨ 8×7 ⑩ 9×5 ⑪ 3×6 ⑫ 5×5 ⑬ 4×3 ⑭ 8×8 ⑮ 1×9 ⑯ 7×2 ⑰ 4×6 ⑱ 1×6 ⑲ 3×9 ⑳ 9×8 2 El metro Había 6 manzanas en cada bolsa. Una niña compró 7 1 bolsas. ¿Cuántas manzanas compró en total? 3 Yoshie extendió sus brazos y midió su longitud con una cinta. El largo de sus brazos extendidos fue 11 3 grupos de 30 cm y 25 cm más. Longitud de los brazos de Yoshie Inventa un problema para 86 usando las palabras "plato" y "caramelo". 11 4 Longitud(2) Mide el largo y el ancho del cuadro de abajo y exprésalos en milímetros. 30 cm 30 cm 30 cm 25 cm ¿Cuántos cm miden sus brazos extendidos? 100 cm es “1 metro” y se expresa como 1 m. 1 m = 100 c m 8 El metro (m) es otra unidad de longitud. 48 49 30 cm 30 cm 30 cm 25 cm Cálculo de longitudes 15 cm 1m Una tira de madera de 1m es útil para medir objetos largos. 115 cm= 1 m 15 cm m 1 2 1 Un pedazo de cinta se cortó en 2 partes que midieron 3m, 20cm y 2m respectivamente. 3C m 20 B cm cm 1 2C m 5 Midamos el ancho de una jardinera como la que ① ¿Cuánto mide de largo la cinta original? se muestra. 3m 20cm + 2m ¿Cuántos metros y centímetros mide el ancho? La idea de Tadashi ▼ La idea de Sayuri ▼ ¿Cuántos centímetros son en total? Yo sumo los números con la misma unidad. 3m y 2m dan 5m. C C B 5m y 20cm dan m m cm 3 20 +2 cm. ② ¿Cuál es la diferencia entre las longitudes de las dos 1 Midamos varias cosas usando una cintas? tira de madera de un metro de largo. 2 ¿Cuántos metros y centímetros mide 1 la cinta de abajo? de largo. ¿Cuál es la diferencia entre las longitudes de las ¿Cuántos centímetros son en total? dos cuerdas? 2 1m 50 Hay una cuerda de 13 m de largo y una cuerda de 2m 30 cm Calculemos. ① 24 m+ 15 m ② 23 m 50 cm- 15 m 51 1 Mide las longitudes de estas cintas página 50 (m) C ① ¿Cuántos metros y centímetros miden de largo la cinta roja y la cinta azul? ② ¿Cuántos centímetros miden de largo la cinta roja y la cinta 1 . Escribe las unidades correctas en el ① El grosor de un cuaderno. 3 ② El ancho de un salón de clase. 7 ③ La longitud de un escritorio. 60 ④ La altura del edificio de un colegio. 20 2 Pon las siguientes medidas en orden, del más largo al más corto. 3m 7 cm 2 m 80 cm azul? 2 Calcula las siguientes longitudes. ① 8 m 20 cm+3 m ② 2 m 30 cm+25 cm ③ 7 m 15 cm−4 m ④ 1 m 72 cm−40 cm 3 Mide las longitudes de varios objetos que están a nuestro alrededor. • Primero inténtalo adivinando. página 51 página 50 3 Haruko midió el ancho y la altura de un librero. Ancho: una tira de madera de 1 m cupo una vez y quedaron 28 cm. Altura: Una tira de madera de 30 cm cupo dos veces y quedaron 10 cm. • Luego mídelos para comprobar. ① ¿Cuántos metros y centímetros miden el ancho y la altura del librero? ② ¿Cuál es más largo, el ancho o la altura? ¿Cuántos centímetros más largo? ■ Ir a la página 54 52 ■ Ir a la página 80 ■ Ir a la página 86 53 La regla larga ● 14 Números mayores que 1000 Construye una regla larga con cinta de papel y mide las longitudes de varios objetos. Cuenta el número de granos de arroz que hay en un tazón. Haz una escala de 1 cm, 10 cm y 1 m usando colores diferentes . Recuerda cómo contar números hasta 1000. ¿Cuántos grupos de 1000 se forman? 54 10 grupos de 100 son 1000. ¿Cuántos grupos de 1000 hay? 55 Cuando hay 2 grupos de 1000, lo llamamos "dos mil" ③ ¿Cómo puedes decir el número total de granos de arroz? El número que está formado por la suma de dos mil, trescientos, cuarenta y seis se llama ``dos mil trescientos cuarenta y seis”. Este número se escribe así: 2346. El lugar que ocupa el 2 en el número 2346 se llama "unidades de millar". 1 ¿Cuántos millares centenas decenas unidades dos2mil tres cientos 3 cuarenta 4 2 3 4 seis 6 6 hay? ① ¿Cuántos grupos de 100 hay? ② ¿Cuántos grupos de 1000 se forman? 2 ¿Cuántas hojas de papel hay? ones place unidades 56 tens place decenas 9 grupos de cien. centenas hundreds place ② 3 grupos de mil y thousands millaresplace ① ① ② ③ ③ 5 grupos de mil y 7 grupos de diez. 57 unidades cada caja tiene 10 decenas Cada paquete tiene 10 cajas y centenas . millares 3 Cuenta el número de 8 ¿Qué número es mayor? ① 4950,5190 4900 . ① ¿Cuántos hay? 5100 5200 4950 ② ② ¿Cuántos grupos de 100 se 4 ¿Cuáles son los siguientes números? ① El número que se construye con 7 grupos de 1000. ② El número que se construye con 60 grupos de 100. 5 Expresa con palabras los siguientes números. ① 6472 ② 6 Escribe las siguientes cantidades usando números arábigos. 1509 ④ 7003 ③ ④ 8400 millares centenas decenas unidades 8500 8600 9253,9238 9220 9230 millares centenas decenas unidades 9240 9250 millares centenas decenas unidades 5769,5764 5750 ¿Qué lugar hace más fácil ver cuál es mayor? 5190 8340,8610 8300 necesitan para obtener 2300? 3085 ③ 5000 millares centenas decenas unidades 5760 5770 5780 ① Tres mil setecientos cuarenta y cinco. ② Siete mil veintiocho. ③ 7 Tres mil uno. 9 ④ Cinco mil números del más chico al más grande. Escribe las siguientes cantidades usando números arábigos. ① El número que es la suma de 3 grupos de 1000, 9 grupos de 100, 2 grupos de 10 y 7 grupos de 1. ② El número que es la suma de 6 grupos de 1000 y 2 grupos de 10. ③ El número que es la suma de 9 grupos de 1000 y 1 grupo de 1. 58 Traza líneas para conectar estos ④ El número que es la suma de 18 grupos de 100. 5500 5600 5400 5200 5100 4100 5700 5300 5000 5800 4900 4800 3800 4600 4700 3900 4500 4000 4200 4300 4400 59 10 Usa la recta numérica de abajo para responder lo siguiente. ① ¿Qué números corresponden a , y ? 1 ¿Cuántas hojas de papel hay? página 57 ② Dibuja una ↑ para señalar el punto de la recta que 10 corresponde a 3200. ③ 1000 1000 1000 Escribe el número que es 800 unidades mayor que 3200. Luego escribe el número que es 300 unidades menor que 3200. 11 ¿Cuántas hojas de papel hay? Mil, dos mil, tres mil, … nueve mil, ¿Cuál es el que sigue? El número formado por 10 grupos de 1000 se llama "diez mil" y se escribe 10 000. 100 10 10 10 página 58 2 Lee los siguientes números. ① 7492 3 Escribe los siguientes números. ① El número que es la suma de 7 grupos de 1000, 5 grupos de ② 2018 ③ 6501 ④ 8001 página 58, 60 100 y 4 grupos de 1. ② El número que es la suma de 50 grupos de 100 y 50 grupos de 1. ③ El número que es 1000 unidades mayor que 8000. ④ El número que es 500 unidades menor que 4000. 4 Para el número 5800, escribe los números correctos en el de abajo. páginas 58,60 ① El 5 indica que hay 5 grupos de ② 5800 se forma con ③ El número que es 200 unidades mayor que 5800 se construye a partir de 60 10 . grupos de 100. grupos de 1000. 61 1 ① Escribe los siguientes números. El número que es la suma de 8 grupos de 1000 con 4 grupos de 100 y 6 grupos de 1. El número que es la suma de 43 grupos de 100 y 60 grupos de 1. ③ El número que es 1000 unidades mayor que 5000. ④ El número que es 200 unidades menor que 7000. Prepara 2 tarjetas para cada uno ① de abajo. Revuelve las tarjetas y ② Cada niño toma una tarjeta y la pone en uno de los 4 cuadrados. ③ ① 7 indica que hay 7 grupos de . ② 7400 es un número que es Haz esto 4 veces para completar todos los cuadrados. grupos de 100. ③ El número que es 400 unidades menor que 7400 está formado por grupos de 1000. 3 Escribe los números que faltan en los 1 al 9 . colócalas mirando hacia abajo. Analiza el número 7400, escribe los números correctos en el ● de los números del ② 2 ¿Cuál número es mayor? ④ El niño que construye el número mayor es el ganador. de manera que la respuesta en cada caso sea 7620. ① El número que es grupos de 10. ② El número que es la suma de de 100 y grupos de 10. ③ El número que es la suma de grupos de 1000 y ④ El número que es la suma de grupos de 100 y ■ Ir a la página 63 62 grupos de 1000, ■ Ir a la página 81 de 10. No estoy seguro donde poner el 7. Cambia las reglas del juego de modo que quien construye el número menor sea el ganador. Juega de nuevo. de 10. ■ Ir a la página 87 63 15 Triángulos y cuadriláteros La figura que se construyó usando 3 líneas rectas se llama "triángulo". La figura que se construyó usando 4 líneas rectas se llama "cuadrilátero". 3 Encuentra los triángulos y cuadriláteros. Líneas rectas 1 Usa un cordón para hacer la cuna del gato como se muestra arriba. 2 Haz una línea recta. ① Extiende una banda elástica. ② Dobla un pedazo de papel. La línea que es como una banda elástica estirada, se llama "línea recta". 3 Dibuja una línea recta usando una regla y verifica que la línea esté realmente recta comparándola con una cuerda estirada. 64 2 Separa en 2 grupos las figuras que se formaron con líneas rectas. La jirafa está encerrada por 3 líneas rectas. Encuentra las figuras que no son triángulos ni cuadriláteros. Piensa por qué razón estas formas son diferentes. El venado está encerrado por 4 líneas rectas. 66 67 4 Dibuja varios triángulos y cuadriláteros uniendo los puntos con líneas rectas. 5 Corta el papel para hacer las siguientes formas. ① 2 triángulos. 1 Busca triángulos y cuadriláteros. 2 Dibuja varios triángulos y cuadriláteros uniendo los puntos con líneas rectas. página 67 página 68 ② 2 cuadriláteros. ③ Un triángulo y un cuadrilátero. 6 Triángulos y cuadriláteros 1 Busca objetos que tengan forma de triángulo o cuadrilátero. Trata de encerrar cada animal con la menor cantidad de líneas. Conecta los puntos utilizando líneas rectas para encerrar a cada animal. 65 68 69 16 Suma y resta 1 Colorea con rojo los triángulos y con azul los cuadriláteros. 1 Compara los dos cálculos siguientes. ① 2 8 niños estaban jugando y 4 niños más se les unieron. pero 4 niños se fueron a casa. ¿Cuántos niños hay en total? ¿Cuántos niños quedaron? Todos los niños : Recorta las figuras que tienen la misma forma y diseña patrones. Primeros niños : 8 Niños que quedaron 8+4= ② 3 Construye varios triángulos uniendo los puntos con líneas rectas. Ejemplo Hay 6 flores rojas y 7 Niños que se fueron: 4 12-4= Hay flores rojas y blancas. ¿Cuántas flores hay en flores blancas. total? ¿Cuántas flores rojas hay? flores blancas 6+7= ■ Ir a la página 88 Niños que quedaron : El total de flores es 13. Hay 7 flores rojas : 6 ■ Ir a la página 82 Todos los niños : 12 flores blancas. Total de flores: 70 12 niños estaban jugando, Total de flores : 13 flores rojas : flores blancas : 7 13-7= La suma y la resta tienen efectos opuestos. 71 2 3 27 pasajeros iban en un Yoshiko tiene unas fichas. Le dio 6 a su hermana y le autobús. quedaron 18. Subieron más pasajeros, ahora hay 34 en total. ¿Cuántas fichas tenía al ¿Cuántos nuevos pasajeros principio? subieron? En este problema, se usó la palabra "quedaron", así que ésta es una resta, ¿estás de acuerdo? Dice "en total", pero ¿es éste un cálculo de suma? Total de pasajeros : Número de pasajeros que iban en el autobús: ① Elnúmero quedio: : El número que dio Número de pasajeros que subieron después : Representa a los pasajeros que subieron después con ☐ y escribe una expresión matemática con ☐. ② : 4 ① Número total : 15 El número que dió : Escribe en la gráfica los números que conoces y haz la operación para encontrar cuántos pasajeros Construye problemas mirando las figuras de abajo. ② Número Total : 18 subieron después. 72 El número que quedó : 9 Número Original : 8 : El número que compraron 73 17 Resumen del Segundo Grado 1 Construye varios números 3 Hagamos problemas de multiplicación para 46. Un problema para 1368 4 6 Hay 4 fresas en cada plato. usando tarjetas marcadas con ¿Cuántas fresas hay en 6 platos? 1 , 3 , 6 y 8 . Y construye: El número mayor ……… ① Hagamos otro problema cambiando los números en el ② Haz otro problema cambiando . . El número menor ……… 2 Calcula. Un problema para 6 5 Hay 6 rebanadas de pan en cada bolsa. ¿Cuántas rebanadas de pan hay en 5 bolsas? Suma cada pareja de números y escribe la suma en el recuadro que está arriba de ellos. 4 Inventa 4 multiplicaciones en las que todos los dígitos sean diferentes. En cada pareja de números resta el número menor del mayor y escribe la respuesta en el recuadro que está debajo de ellos. 74 36=18,39=27, 57=35,49=36. ¡Oh no!, usé el 3 dos veces. 36=18, 39=27, 57=35. Aún puedo usar 0, 4, 6 y 9. = = = = Eso significa que puedo terminar con 88=64. 75 5 Mide la longitud de estas líneas. ¿Cuántos mm miden de largo? 6 ¿Cuál unidad es mejor para medir las longitudes de abajo? m,cm,mm ① El largo de un pasillo. 7 ② El grosor de un libro. Dibuja varios triángulos y cuadriláteros uniendo los puntos con líneas rectas. 76 Inventemos problemas de multiplicación 11 ¿Qué estás haciendo? 12 ¿Puedes encontrar el cofre del tesoro? 13 ¿Qué día es? 14 Dibuja conectando los puntos 15 Ordenemos los asientos 11 Encuentra la respuesta para 3 × 12 12 Calculando longitudes 13 Cálculos con dinero 14 Doblando y cortando 15 77 Inventemos problemas de multiplicación ● Inventa un problema de multiplicación. Puedo hacer uno colocando el mismo número de algo en cada caja. ● ¿Qué estás haciendo? ● Haz cada una de las multiplicaciones que están a la izquierda. Si encuentras la respuesta en la misma fila del lado derecho colorea O en cada plato. ese casillero. 62,56,66,68,37,74,83 32 30 24 12 27 28 36 48 21 46,67,96,27,57,49,58 54 30 72 22 25 38 12 56 42 88,27,47,79,85,99,76 63 62 50 13 67 21 83 28 43 92,58,89,49,57,66,97 45 63 72 36 74 30 18 62 38 69,94,58,63,77,22,88 62 56 38 49 50 64 16 93,89,65,38,84,92,43 21 73 16 27 26 30 13 10 32 64,82,29,88,98,23,66 24 64 16 6 73 22 36 18 62 76,74,82,73,87,92,33 6 2 9 59,38,86,48,98,77,29 40 41 35 73 32 16 34 28 42 haz un "libro de la multiplicación" 97,84,36,99,87,64,72 63 32 14 81 62 16 56 28 59 y muéstraselo a tu grupo. 68,64,48,78,83,39,47 34 26 23 56 21 41 27 57 29 86,77,97,28,83,39,65 41 67 48 21 42 28 49 19 35 93,69,72,56,79,82,48 52 14 40 28 12 66 54 33 21 36,47,76,37,75,24,98 8 67,96,78,63,72,39,79 18 45 19 42 17 64 54 65 58 46,66,74,95,78,88,99 21 36 64 26 59 87 45 58 69 Después de inventar el problema, 48 26 16 26 29 36 2 43 20 58 11 19 4 35 32 74 Pon el libro de cabeza. Verás que los cuadrados forman 2 números. ¿Qué haces a esa hora cada día? ¿Qué estás haciendo? 78 79 ¿Qué día es? ¿Puedes encontrar el cofre del tesoro? ● Escribe las siguientes cantidades usando números arábigos. Entrada Reglas Partida Horizontal Vertical ② Dos mil ochocientos cincuenta y uno. Usa una regla y un lápiz. Debes cambiar de dirección después ① Cinco mil ochocientos sesenta y cuatro. ③ La respuesta a 9 8. ② Doscientos noventa y tres. ④ La respuesta a 88 +8. ⑤ El número que es la suma de 5 grupos de 100 y 11 grupos de moverte 3 cm. No debes cruzar sobre rocas, árboles y agujeros. ⑤ El número que es 80 unidades menor que 6000. ⑥ El número que es la suma de 16 grupos de 100 y 5 de 1. ⑦ El número que es la suma de 2 grupos de 100, 9 grupos de grupos de 1. ⑦ El número que es 19 unidades más grande que 200. 10 y 6 grupos de 1. ⑧ El número que es una unidad menor que 100. ⑨ El número que es la suma de 12 grupos de 100 y 7 grupos de 1. ⑩ Cuatro mil novecientos cinco. Encuentra el camino más corto Cofre del Tesoro 80 Escribe los números correctos en el Mes : a b , Día : c d . Es el día . en Japón. 81 Dibuja conectando los puntos ● Ordenemos los asientos Dibuja muchos triángulos y cuadriláteros uniendo puntos mediante líneas rectas. Combina triángulos y cuadriláteros. 19 niños van en un tren. El tren tiene una sección con filas de 3 asientos y otra con filas de 2 asientos. ¿Cómo pueden sentarse de modo que ninguno quede solo? ¿Hay otra forma? 35 y 22 es una buena forma de elegir asientos. Los niños usan 3 y 2 filas de 3 y . Mediante el uso de la multiplicación combinamos filas de 3 y filas de 2. Todos podemos sentarnos de manera que nadie esté solo. filas de 2. ¿En serio? ¿Puedes hacer esto para cualquier número de niños? Trata de nuevo con otros números. Yo dibujé un barco. 82 83 Encuentra la respuesta para 312 ② Vamos a obtener la respuesta de 312 usando lo que hemos aprendido y lo que descubrió Eiko. Encuentra la respuesta para 312 usando 3□. ① La idea de Nobuaki ▼ Observa la tabla de multiplicación del 3. ¿Notas cosas interesantes? Cuéntale a los demás lo que estás pensando. 31= 3 Las respuestas aumentan en 3 cada vez: 39=27,310=30, 311=33. Entonces 312=36. La idea de Chizuko ▼ 32= 6 33= 9 34=12 35=15 36=18 37=21 38=24 39=27 Si sumamos la respuesta a la pregunta 3 9 y la respuesta a 3 3, podemos obtener la respuesta a la pregunta 3 12. Es decir, 27 + 9 = 36. la idea de Masakuni ▼ Si dividimos la tabla en 6, 36=18. Como 312 son 2 grupos de 36, obtenemos 18+18=36. El descubrimiento de Eiko ▼ La suma de la respuesta a 3 2 y la respuesta a 3 3 es la respuesta a 3 5. 84 85 Calculando longitudes 1 La altura de una jirafa es 3 m 30 cm y la altura de un Cálculos con dinero 1 Si compro una goma en 60 yenes y un mono es de 70 cm. ¿Cuál es la diferencia en metros y cuaderno a 80 yenes, ¿cuántos yenes centímetros de sus alturas? necesitaré? 3 m 30 cm− 70 cm La Idea de Takeshi ▼ 60 + 80 3 m 30 cm es igual a 330 cm. Trata de pensar en la cantidad de monedas de 10 yenes que hay. Si uso bloques de10, puedo pensar 330-70 como 33-7. 2 Yukie tiene 500 yenes y Satoshi tiene 300 yenes. Sabemos que 33-7=26. ① ¿Cuántos yenes tienen ellos en total? Como 26 significa 26 grupos de 10, tenemos 260 cm que es igual + a 2 m 60 cm. Trata de pensar en la cantidad de monedas de 100 yenes que hay. la Idea de Toshiko▼ 3 m 30 cm puede separarse en 2 m y 1 m 30 cm. ② ¿Cuál es la diferencia del dinero que tiene De 1 m 30 cm-70 cm, cada uno? obtenemos 130 cm-70 cm=60 cm, y finalmente 2 m y 60 cm dan 2 m 60 cm. 2 86 Haz los siguientes problemas. 3 Resuelve los siguientes problemas. ① 1 m 40 cm+70 cm ② 2 m 10 cm+1 m 50 cm ① 300+600 ② 700+800 ③ 4 m 10 cm-80 cm ④ 5 m 20 cm-1 m 80 cm ③ 900-400 ④ 1500-600 87 Juego con la multiplicación ① Doblando y cortando columna fila Dobla varias hojas de papel de color, dibuja 2 líneas rectas Dado para las columnas. como se muestra y corta la figura. Dado para las filas. ¿Qué tipos de figuras ves? ① escribe las respuestas en los cuadrados. Luego cubre las respuestas con ① Observa la figura que obtuviste y di a los demás lo que ves. ② Multiplica los números en la fila por los números en las columnas y 30 fichas. ② Busca figuras similares en nuestro alrededor. Lanza los 2 dados a la vez. Multiplica los 2 números y di la respuesta. Si la respuesta es correcta, obtienes la ficha de ese cuadrado. ③ Si no hay fichas sobre el cuadrado que eliges, tienes que poner una ficha sobre él. ④ Acuerda con tu compañero el número de veces que van a lanzar el dado y juega en turnos. ⑤ 88 El niño que obtiene más fichas es el ganador. 89 Juego con la multiplicación ② Este es un juego que puede disfrutar todo el grupo. ① Escribe cualquier número de las tablas de multiplicar en una tabla de 1 56 14 7 81 5 4 Primera vez Segunda vez Tercera vez Cuarta vez 6 25 42 3 2 28 32 20 16 16 cuadrados. ② Un alumno elige una tarjeta de un grupo de tarjetas de multiplicación. ③ El alumno hace la multiplicación que 4×5 4×5 muestra la tarjeta y encierra en un ○ 5 la respuesta si está en la tabla que hiciste. 3 2 32 20 16 ④ Obtienes 1 punto cuando hay un ○ en todos los números de una fila, columna o diagonal. 1 56 obtiene el mayor número de puntos es 14 7 el ganador. 81 5 ⑤ Elije 40 tarjetas en total. El que 4 6 25 42 3 2 28 32 20 16 ● Trata con una tabla de 25 cuadrados. ¿Qué número debo escribir en el centro de la tabla? 1 punto 90 91 Tabla de multiplicación multiplicador multiplicando fila del 1 fila del 2 fila del 3 fila del 4 fila del 5 fila del 6 fila del 7 fila del 8 fila del 9 Ilumina las respuestas usando diferentes colores. Usa color gris si el número en el lugar de las unidades es 0, amarillo si el número es 1, y así sucesivamente. Hay 9 colores diferentes en la fila del 1. ¿Cuántos colores usaste en la fila del 5? multiplicador multiplicando 92 1 2 3 4 5 6 7 8 9 5 6 7 8 9 fila de 1 1 1 2 3 4 fila de 2 2 2 4 6 8 fila de 3 3 3 6 9 fila de 4 4 4 8 fila de 5 5 5 10 15 20 25 30 35 40 45 fila de 6 6 6 12 18 24 30 36 42 48 54 10 12 14 16 18 12 15 18 12 16 21 24 27 20 24 28 32 36