Autoevaluación Circulación renal y Filtración Glomerular
Anuncio
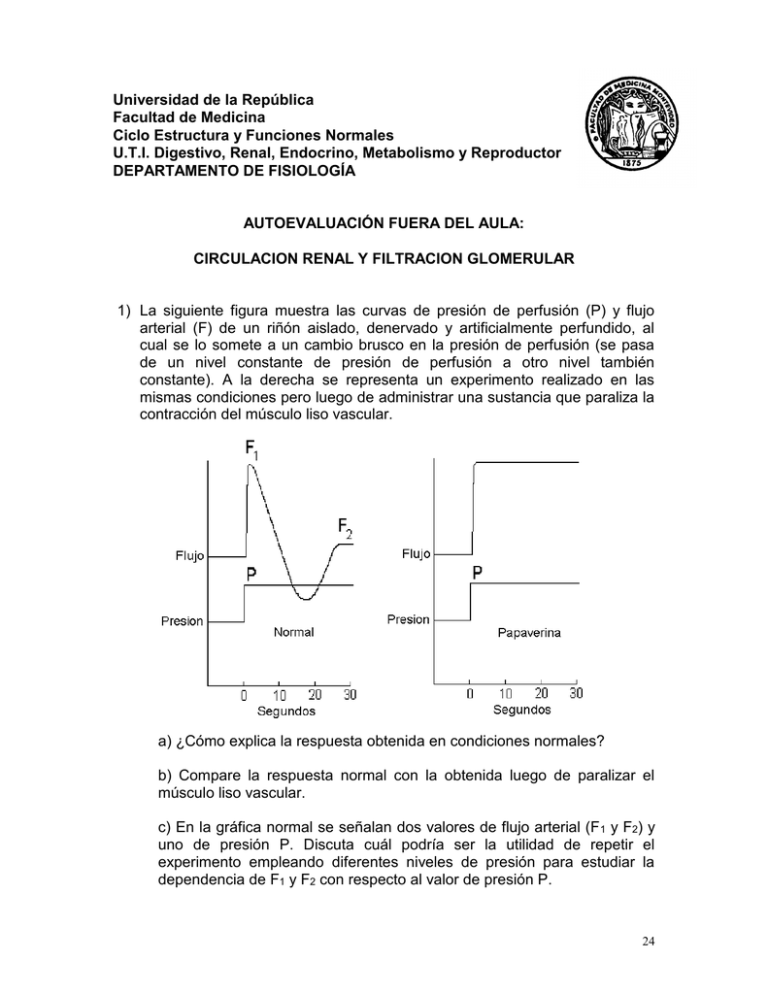
Universidad de la República Facultad de Medicina Ciclo Estructura y Funciones Normales U.T.I. Digestivo, Renal, Endocrino, Metabolismo y Reproductor DEPARTAMENTO DE FISIOLOGÍA AUTOEVALUACIÓN FUERA DEL AULA: CIRCULACION RENAL Y FILTRACION GLOMERULAR 1) La siguiente figura muestra las curvas de presión de perfusión (P) y flujo arterial (F) de un riñón aislado, denervado y artificialmente perfundido, al cual se lo somete a un cambio brusco en la presión de perfusión (se pasa de un nivel constante de presión de perfusión a otro nivel también constante). A la derecha se representa un experimento realizado en las mismas condiciones pero luego de administrar una sustancia que paraliza la contracción del músculo liso vascular. a) ¿Cómo explica la respuesta obtenida en condiciones normales? b) Compare la respuesta normal con la obtenida luego de paralizar el músculo liso vascular. c) En la gráfica normal se señalan dos valores de flujo arterial (F 1 y F2) y uno de presión P. Discuta cuál podría ser la utilidad de repetir el experimento empleando diferentes niveles de presión para estudiar la dependencia de F1 y F2 con respecto al valor de presión P. 24 2) En la figura, se muestra la correspondencia entre flujo sanguíneo arterial y presión de perfusión (P). Con círculos vacíos se muestra la magnitud del flujo inicial transitorio (F1) en función de la presión de perfusión. Con círculos llenos se representan los valores de flujo luego de un período de adaptación (F2). Flujosangierltvo(%) a) ¿Qué consecuencias tiene el cambio de presión en la respuesta vascular renal? b) ¿Cómo se denomina este 1 6 0 fenómeno? F 1 1 4 0 c) ¿Qué teorías conoce que F pretendan explicar dicho 2 1 2 0 fenómeno? 1 0 0 d) ¿Qué zona del riñón juega un papel cuantitativamente más 8 0 importante en esta respuesta? e) Si se grafica el flujo 6 0 resultante contra la presión de 4 0 perfusión en el preparado paralizado por papaverina se 2 0 obtiene una curva similar a la de círculos vacíos. Discuta el 0 significado de este resultado, 0 2 0 4 0 6 0 8 0 1 0 0 1 2 0 1 4 0 1 6 0 teniendo en cuenta las hipótesis P r e s i o n d e p e r f u s i o n ( m m H g )explicativas que mencionó en c. 3) Considere la siguiente fórmula que representa la ecuación de filtración (expresión del principio de Starling simplificado). IFGN = Kf . Puf = Kf . ( P - ¶) Donde: IFGN = índice de filtración glomerular por nefrona. Kf = coeficiente de ultrafiltración por unidad de área Puf = presión neta de ultrafiltración que corresponde a la diferencia entre los valores de P (gradiente de presión hidrostática) y ¶ (gradiente de presión oncótica) promediados en toda la longitud del capilar glomerular. 25 Teniendo en cuenta los siguientes valores de presión hidrostática (P) y presión oncótica (¶) obtenidos en experimentos realizados en ratas: Sector Capilar Glomerular Pcg PT ¶cg Puf ___________________________________ Extremo aferente 50 13 20 17 Extremo eferente 48 13 35 0 ___________________________________ Pcg = presión en el capilar glomerular PT = presión tubular y en la cápsula de Bowman ¶cg = presión oncótica en el capilar glomerular Puf = presión de ultrafiltración a) grafique las curvas correspondientes a P y ¶ en función de la distancia a lo largo del capilar glomerular desde el punto de inicio de la arteriola aferente. b) indique qué zona de la gráfica ilustra la magnitud de Puf y cuál es su valor inicial c) Indique cómo y por qué cada una de las variables del extremo derecho de la ecuación de Starling cambia en función de la distancia a lo largo del capilar glomerular (CG). d) Describa en forma cualitativa cómo las variaciones en la presión del CG, tasa de flujo plasmático, concentración proteica plasmática y coeficiente de filtración (Kf), afectan la velocidad de filtración glomerular (VFG). e) Describa cómo la carga eléctrica a nivel del "poro" glomerular afecta la filtración de los solutos y qué solutos son afectados. 26