Conversiones entre los parámetros z, y, h, g, t, s.
Anuncio
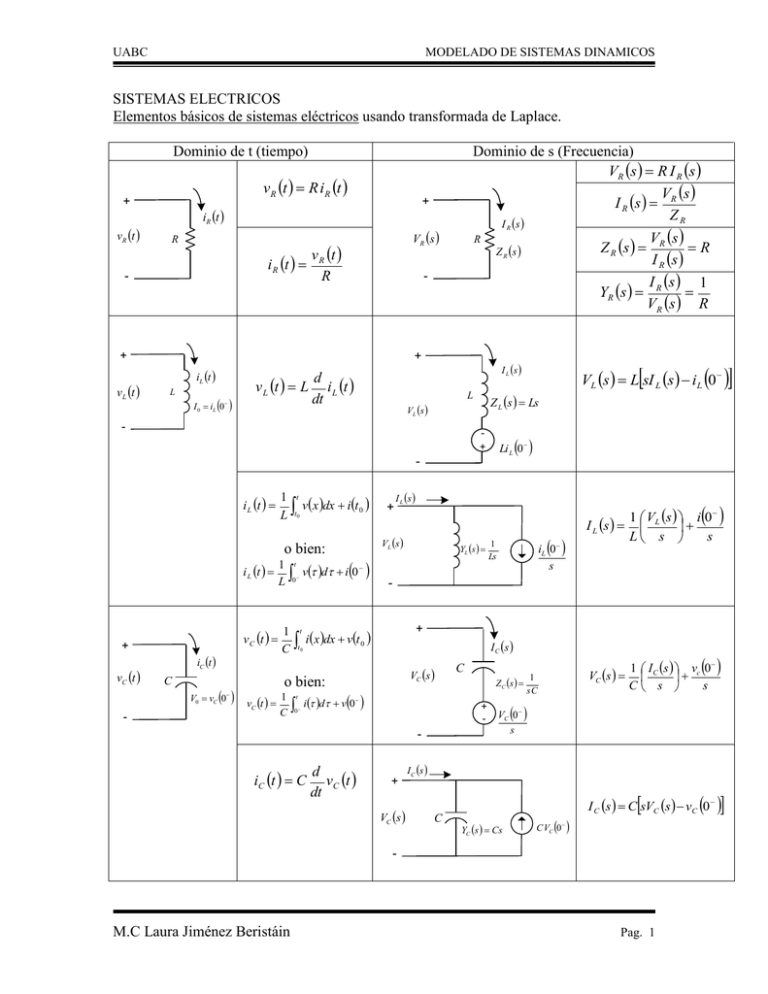
UABC MODELADO DE SISTEMAS DINAMICOS SISTEMAS ELECTRICOS Elementos básicos de sistemas eléctricos usando transformada de Laplace. Dominio de t (tiempo) v R t R iR t + vR t + iR t R V R s v t i R t R R - - + vL t Dominio de s (Frecuencia) VR s R I R s V s I R s R ZR I R s V s R Z R s R R Z R s I R s YR s + iL t L I 0 iL 0 d v L t L i L t dt + - Li L 0 - 1 t v x dx i t 0 L t0 o bien: 1 t i L t v d i 0 0 L v C t + vC t iC t C V0 vC 0 - 1 C + I L s VL s 1 C VC s - d vC t dt C 1 Z C s sC + - 0 iC t C VC s 1 I C s vc 0 C s s iL 0 s I C s 0 i d v0 t 1 Ls 1 VL s i 0 L s s + t o bien: vC t YL s I L s - ix dx vt t0 + VC s VC 0 s I C s C I C s C sVC s vC 0 YC s Cs C VC 0 - M.C Laura Jiménez Beristáin VL s L sI L s iL 0 Z L s Ls L - i L t I L s VL s I R s 1 VR s R Pag. 1 UABC MODELADO DE SISTEMAS DINAMICOS SISTEMAS MECÁNICOS Se dividen en sistemas mecánicos traslacionales y rotacionales. Sistemas mecánicos Traslacionales Ma F Variables x Desplazamiento Variables . . Velocidad angular v x Velocidad . .. a v x Aceleración F M Elementos x Masa: FM .. d 2x Mx 2 dt (Ley de Newton) x1 x2 K F F Rotacionales J T Desplazamiento angular Resorte: F k x2 x1 . .. Aceleración angular TJ .. d 2 J J 2 dt T k 2 1 k (Ley de Hooke) k = Coeficiente del resorte . . x1 x2 b F F b = Coeficiente de fricción viscosa Amortiguador: dx dx F b 2 1 dt dt . d d T b 2 1 b dt dt . . F b x 2 x1 Sistemas mecánicos traslacionales: Definiciones Las variables más comunes utilizadas para describir los movimientos de traslación en sistemas mecánicos son: x desplazamiento (m) v velocidad (m/s) a aceleración (m/s2) f fuerza (N) Otras variables adicionales de interés son: w energía (J) p potencia (W) La potencia aplicada a un móvil que se desplaza a velocidad v es, p =fv y corresponde a la velocidad con que la energía es aplicada o disipada, p = dw/ dt Elementos de los sistemas mecánicos traslacionales Masa M.C Laura Jiménez Beristáin Pag. 2 UABC MODELADO DE SISTEMAS DINAMICOS La segunda ley de Newton establece que la resultante de las fuerzas que actúan sobre un cuerpo es igual a la velocidad de cambio de la cantidad de movimiento, que en el caso más común de masa M constante da lugar a la siguiente ecuación: dv M f dt La energía puede ser almacenada en forma de energía cinética si la masa se encuentra en movimiento y en forma de energía potencial si presenta un desplazamiento vertical relativo respecto a su posición de referencia. La energía cinética vale, 1 wc Mv 2 2 La energía potencial para un campo gravitatorio uniforme vale, wp M g h Fricción Las fuerzas que son funciones algebraicas de la velocidad relativa entre los cuerpos se modelan por elementos de tipo fricción. f C v Donde C tiene unidades de N·s/m y v = velocidad relativa. El sentido de la fuerza de fricción es tal que tiende a oponerse al movimiento relativo. Elasticidad Un elemento mecánico que sufre un cambio de forma cuando se le aplica una fuerza, puede ser caracterizado por un elemento elástico si existe una relación algebraica entre la fuerza aplicada y la elongación producida. El elemento elástico más común es el resorte. La relación entre la fuerza y la elongación es la curva característica del resorte. Para un resorte lineal la curva es una línea recta y por tanto, f Kx donde K es la constante del resorte (N/m). La energía potencial almacenada en un resorte lineal es, 1 wp K x 2 2 Ejemplo Modelar matemáticamente el sistema mecánico indicado en la figura suponiendo que la masa se mueve horizontalmente sin rozamiento apreciable y que el resorte y el elemento de fricción tienen comportamiento lineal. Solución Se sustituyen las fuerzas por su valor en el diagrama de sólido libre, aplicando las leyes de Newton (o el principio de D’Alembert) La suma de todas las fuerzas debe ser nula: con lo que la ecuación diferencial queda de la forma: Sistemas mecánicos rotacionales Definiciones Las variables más comunes para identificar la rotación en sistemas mecánicos son: θ desplazamiento angular (rad) ω velocidad angular (rad/s) M.C Laura Jiménez Beristáin Pag. 3 UABC MODELADO DE SISTEMAS DINAMICOS α aceleración angular (rad/s2) τ par torsor (N·m) Otras variables adicionales de interés son: w energía (J) p potencia (w) La potencia aplicada a un móvil que rota a velocidad ω es, p = τ ω La energía total aplicada es, wt wt 0 p d t t0 Elementos de los sistemas mecánicos rotacionales Momentos de inercia Cuando se aplica la segunda ley de Newton a cada uno de los diferenciales de masa de un cuerpo que está rotando y se integra el resultado a toda la masa del cuerpo se obtiene, para el caso común de momento de inercia constante, . I La energía cinética almacenada en la rotación vale, 1 wc I 2 2 La energía potencial almacenada vale, wp M g h Fricción La fricción rotacional se produce cuando dos cuerpos rotan a diferentes velocidades angulares produciéndose un rozamiento entre ellos. τ = B ω Donde B tiene unidades de N·m·s y ω = ω2- ω1 El par torsor de fricción tiende a reducir la velocidad angular relativa ω Elasticidad La elasticidad a rotación está generalmente asociada a resortes de torsión o ejes delgados que presentan una relación algebraica entre el par torsor aplicado y el ángulo girado. Para un resorte de torsión lineal, τ = k θ donde k es la constante del resorte (N·m). θ, ω, α, τ La energía potencial almacenada en un resorte a torsión es para un caso lineal, 1 2 w p K 2 Palancas Una palanca ideal es una barra rígida que pivota respecto a un punto y no presenta masa, fricción, momento ni energía almacenada. Las palancas permiten transmitir el movimiento de rotación en sus extremos. Si el ángulo rotado es pequeño, el movimiento en los extremos se puede considerar traslacional, y se calculan por medio de relaciones trigonométricas. Engranajes M.C Laura Jiménez Beristáin Pag. 4 UABC MODELADO DE SISTEMAS DINAMICOS Un engranaje ideal trasmite la rotación y no presenta momento de inercia, energía almacenada ni fricción. El tamaño relativo de los engranajes produce una proporcionalidad constante entre los desplazamientos angulares, velocidades angulares y pares torsores trasmitidos. Para el análisis de sistemas puede considerarse la simplificación de tratar los engranajes como discos tangentes en un punto que ruedan sin deslizamiento relativo. Ejemplo Modelar matemáticamente el sistema mecánico indicado donde la entrada es el par torsor τa y la salida el ángulo girado θ Solución Se sustituyen los pares torsores por su valor en el diagrama de sólido libre. Se deben tener siempre en cuenta las leyes de interconexión; el principio de D’Alembert, la ley de acción y reacción y la ley de los desplazamientos angulares. La suma los pares de torsión debe ser nula. Reordenando términos se obtiene un sistema de 2º orden clásico con perturbación exterior asociada al par torsor aplicado: M.C Laura Jiménez Beristáin Pag. 5 UABC MODELADO DE SISTEMAS DINAMICOS SISTEMAS ELECTROMECÁNICOS En los sistemas electromecánicos se convierte un trabajo eléctrico en un trabajo mecánico. Como sucede en los motores de CD. Los servomotores consisten de un amplificador, un motor, la reducción de engranaje y la realimentación; se caracterizan por su capacidad para posicionarse de forma inmediata en cualquier posición de dentro de un rango de operación de 180º aproximadamente. Para ello el servo espera un tren de pulsos que corresponden con el movimiento a realizar. La duración del pulso indica el ángulo de giro del motor. Generalmente se utilizan valores de 1 ms a 2 ms, los cuales dejarían al motor en ambos extremos. Efectos de la carga en la dinámica del servomotor La característica más importante del servomotor, es la aceleración máxima alcanzable. Para un par disponible dado, el momento de inercia del rotor debe ser mínimo. El momento de inercia equivalente Jeq referido al eje del motor puede escribirse como: J eq. J m n 2 J L n 1 y beq. bm n 2bL n 1 donde: Jm y bm = momento de inercia y coeficiente de fricción viscosa del motor, repectivamente. JL y bL = momento de inercia y coeficiente de fricción viscosa de la carga, repectivamente. n = relación de engranes entre el motor y la carga. Velocidad del eje actuado o o n Velocidad del eje actuante i i Ra La Va Vb T J ia b ic Motor de CD controlado por armadura s K 2 Va s s La Js La b Ra J s Ra b K b K Va (s ) 1 La s Ra I a (s ) T (s ) K 1 Js b (s ) 1 s (s ) Vb (s ) Kb M.C Laura Jiménez Beristáin Pag. 6 UABC MODELADO DE SISTEMAS DINAMICOS SISTEMAS DE NIVEL Los sistemas de nivel de líquido en un tanque se utilizan en procesos de la industria química; mientras que, los sistemas hidráulicos están relacionados con la potencia producida por el flujo de un fluido (aceite). La relación fundamental que se usará en ambos sistemas es: q Av Donde: q = flujo, A = área de la sección y v = velocidad. Ley de continuidad; establece que el flujo de salida mas la velocidad con que se almacena el líquido debe ser igual al flujo de la entrada. qsal . qs qent. dV dh C Donde: q s (velocidad con la que el líquido es almacenado) dt dt h q sal . (Para flujo laminar) R Definiciones: Número de Reynolds. Relación adimensional de la fuerza de inercia con respecto vD a la fuerza viscosa: No. R ; donde: = densidad de masa del fluido, = viscosidad dinámica, v = velocidad promedio del flujo y D = longitud característica. Flujo laminar (300<No. R<4000), es el flujo dominado por la fuerza de viscosidad, se caracteriza por un movimiento de flujo suave, según líneas paralelas. Flujo turbulento (No. R<2000), es el flujo dominado por las fuerzas de inercia y está caracterizado por un movimiento irregular (como remolino). Resistencia hidráulica, es el cambio en la altura diferencial necesaria para causar un cambio unitario en la razón de flujo. Capacitancia hidráulica. En un elemento físico se define como el cambio en la cantidad de material o distancia requerida para producir un cambio unitario en potencial. Inertancia, se refiere al cambio en potencial necesario para producir una razón de cambio unitaria en la razón de flujo. M.C Laura Jiménez Beristáin Pag. 7 UABC MODELADO DE SISTEMAS DINAMICOS Sistemas de Nivel y sistemas Hidráulicos. Ley de continuidad: qsal . qs qent. dV dh C Donde: q s (velocidad con la que el líquido es almacenado) dt dt 2h1 h2 h (Para flujo laminar) y q sal . (para flujo turbulento) q sal . Rl Rt Flujo laminar Flujo turbulento ql K l h1 h2 qt Kt h1 h2 Variables Kl constante de Variables proporcionalidad ql flujo laminar V volumen Elementos F x Resistencia M hidráulica (R): d h1 h2 Rl dq h h2 1 1 q Kl x1 x2 Capacitancia K hidráulica (C): F F q dV C s k = Coeficiente del resorte dh dh dt . . Inertancia (I): x1 Kt constante proporcionalidad qt flujo turbulento Elementos d h1 h2 2h1 h2 Rt dq q x2 b F F b = Coeficiente de fricción viscosa M.C Laura Jiménez Beristáin de Pag. 8 UABC MODELADO DE SISTEMAS DINAMICOS SISTEMAS HIDRÁULICOS MODELADO MATEMÁTICO DE SISTEMAS HIDRÁULICOS Definición Un sistema hidráulico es aquel sistema en el que un fluido (generalmente considerado incompresible) fluye. En general, un análisis matemático exacto no es viable debido a las características no lineales y la naturaleza distribuida del fluido. Sin embargo, se pueden realizar estudios aproximados basados en modelos de parámetros concentrados y linealizando las ecuaciones resultantes. En gran parte de los problemas reales, los sistemas hidráulicos permanecen alrededor de un punto de operación específico del proceso. Por ello permiten una sencilla linealización utilizando variables incrementales. Las variables más comunes utilizadas en los sistemas hidráulicos son: w velocidad del flujo volumétrico (m3/s) v volumen (m3) h altura (m) p presión (N/m2) Para utilizar como variable la presión relativa se suele escoger como referencia la presión atmosférica. a p t p t p = ) ( ) ( * (1) donde p*(t) es la presión relativa y pa es la presión atmosférica. Elementos de los sistemas hidráulicos Capacidad Cuando un líquido es almacenado en un recipiente abierto, existe una relación algebraica entre el volumen total del líquido y la presión en la base del recipiente. La capacidad hidráulica es la relación entre el incremento del volumen de fluido y la variación de presión producida en el fondo del recipiente Para un recipiente de forma arbitraria con área transversal A(h), donde h es la altura desde la base, la capacidad hidráulica C(h) puede calcularse según la siguiente expresión: La presión absoluta en la base del recipiente es: a p h g p + = ρ (3) Para obtener las velocidades de variación del volumen, altura o presión a lo largo del tiempo, se realiza un balance del flujo de masa en el elemento: La cantidad de líquido almacenada en el recipiente puede ser expresada de manera equivalente por v, h y p. En un caso general en el que A(h) y C(h) son variables con la altura el modelo del sistema tiene un comportamiento no lineal. Resistencia Cuando un líquido fluye a través de una tubería, atraviesa una válvula o un orificio, existe una pérdida de presión asociada a la disipación de energía. Normalmente esta pérdida de presión obedece a una ley no lineal respecto al flujo del tipo: p k w = (7) donde k es un parámetro constante que depende de las características de la tubería, válvula u orificio. M.C Laura Jiménez Beristáin Pag. 9 UABC MODELADO DE SISTEMAS DINAMICOS La resistencia hidráulica R del elemento es la relación entre la pérdida de presión y su variación de caudal asociada. Puede calcularse como la inversa de la pendiente en ese punto de la ecuación constitutiva del elemento. Para linealizar una ecuación constitutiva de la resistencia hidráulica alrededor del punto de operación, se aproxima la función no lineal por un desarrollo en serie de Taylor de orden 1: sobre el que se puede introducir el concepto de resistencia hidráulica: El modelo lineal aproximado en variables relativas puede representarse como: El valor de la resistencia R puede expresarse en función de p ó w : Fuentes de energía Para sistemas hidráulicos, la fuente de energía es generalmente una bomba que obtiene la potencia a partir de un motor eléctrico. El caso más común es el de bombas centrífugas a velocidad constante, cuyas curvas características típicas son de la siguiente forma: Para modelar una bomba a velocidad constante en un modelo lineal, se debe evaluar primero el punto de operación calculando p y w . Para pequeños desplazamientos alrededor del punto de operación, puede también linealizarse la ecuación característica de la bomba, de manera similar a lo indicado para la resistencia. Ejemplo La resistencia R representa la pérdida de carga en la tubería por unidad de caudal. El caudal que sale del depósito Q está relacionado con la presión hidrostática (o altura del nivel de agua) y con la resistencia. Suponiendo que la ecuación característica de la perdida de carga en la válvula es aproximadamente lineal, se desea modelar matemáticamente el sistema, encontrar el punto de equilibrio y estudiar su comportamiento en movimiento libre, así como la respuesta del sistema ante entradas de caudal q(t) escalón y rampa. Solución Para una resistencia lineal el caudal que sale del depósito vale Haciendo un balance de masa en el interior del depósito obtenemos la ecuación diferencial del sistema El punto de equilibrio se alcanzará cuando: Para pequeños desplazamientos alrededor del punto de equilibrio, el sistema se comporta como un sistema lineal de orden 1 con tiempo de respuesta T = (R·A): Movimiento libre: M.C Laura Jiménez Beristáin Pag. 10 UABC MODELADO DE SISTEMAS DINAMICOS Respuesta ante entrada escalón E= q: Respuesta ante entrada rampa de pendiente A M.C Laura Jiménez Beristáin Pag. 11 UABC MODELADO DE SISTEMAS DINAMICOS SISTEMAS NEUMÁTICOS M.C Laura Jiménez Beristáin Pag. 12 UABC MODELADO DE SISTEMAS DINAMICOS SISTEMAS TERMICOS MODELADO MATEMÁTICO DE SISTEMAS TÉRMICOS Definición Un sistema térmico es aquel sistema que involucra almacenamiento y flujo de calor. Los modelos matemáticos utilizados en los sistemas térmicos sencillos están basados en las leyes fundamentales de la termodinámica. En general, los sistemas térmicos son distribuidos pero el modelado más sencillo utiliza modelos de parámetros concentrados. Las variables más comunes utilizadas en los sistemas térmicos son: θ temperatura (ºC) q flujo de calor (J/s ó w) Es muy frecuente trabajar con temperaturas relativas respecto a una temperatura de referencia fija θREF que suele ser la temperatura ambiente o una temperatura de equilibrio del sistema. Elementos de los sistemas térmicos Capacidad Existe una relación algebraica entre la temperatura de un cuerpo y el calor almacenado en él. Si no se consideran cambios de fase, esta relación puede tomarse como lineal dentro de un rango de temperatura. La capacidad térmica es la relación entre el calor suministrado a un cuerpo y el cambio de temperatura producido. De esta manera, si qe(t)-qs(t) es el flujo neto de calor en un cuerpo en cada instante de tiempo, la variación de temperatura producida por ese flujo de calor vendrá determinada por la capacidad térmica del cuerpo, según el siguiente balance: o de otra forma: Según la definición de la capacidad térmica C tiene unidades de J/ºC. Para un cuerpo de masa M es el producto de su calor específico ce por su masa. Se ha considerado constante la temperatura del cuerpo en todos sus puntos. En el caso de que existan grandes variaciones de temperatura en el cuerpo, se debe modelar como varios elementos de temperatura constante. Resistencia La conducción del calor entre dos cuerpos conectados se produce a una velocidad proporcional a su diferencia de temperatura. El flujo de calor por conducción desde un cuerpo a temperatura è1 hasta otro cuerpo a temperatura è2 obedece la siguiente ley: donde R es la resistencia térmica del camino entre los dos cuerpos (ºC·s/J) ó (ºC/w) Si el camino de unión tiene un área transversal A y longitud l, la resistencia térmica puede evaluarse de manera simplificada como: donde á es la conductividad térmica del material. M.C Laura Jiménez Beristáin Pag. 13 UABC MODELADO DE SISTEMAS DINAMICOS La ecuación de la resistencia es válida siempre que el cuerpo modelado como resistencia térmica no almacene el calor. En caso contrario el modelo debería añadir también un elemento tipo capacidad. Fuente de calor En sistemas térmicos la fuente de energía es un elemento que genera un flujo de calor q(t). Suele representarse simbólicamente como una resistencia eléctrica. Ejemplo La figura muestra una cámara de calentamiento de un fluido con capacidad calorífica C, rodeado de una cámara de aislamiento que tiene una resistencia térmica equivalente R. La temperatura θ en el interior de la cámara puede considerarse uniforme. La fuente de calor introduce un flujo q(t) al interior de la cámara. La temperatura ambiente exterior θa se considera constante. 1. Modelar matemáticamente el sistema 2. Determinar la temperatura de equilibrio 3. Estudiar el efecto de un incremento brusco en el calor suministrado q(t) Solución Las entradas al sistema son q(t) y θa, luego la ecuación de primer orden resultante para este sistema es: Por tanto el punto de equilibrio se producirá cuando el calor aportado por la fuente de calor sea igual al calor que escapa por la resistencia térmica de la cámara de aislamiento: Si se produce un escalón en el flujo de calor, se debe analizar la respuesta de un sistema de 1er orden ante una entrada escalón: M.C Laura Jiménez Beristáin Pag. 14 UABC ANALISIS Y SINTESIS DE REDES Conversiones entre los parámetros z, y, h, g, t, s. A De Z Y H G T S z y z11 z12 z 21 z 22 z 22 z z 21 z z12 z z11 z z z 22 z 21 z 22 1 z11 z 21 z11 z11 z 21 1 z 21 z 22 z12 1 z12 y 22 y y 21 y y12 y 21 y 22 1 y11 y 21 y11 z12 z11 z z11 y z z 21 z 22 z 21 z z12 z11 z12 M.C Laura Jiménez Beristáin y 22 y 21 y 22 y12 y y11 y y11 z12 z 22 1 z 22 h y 22 y 21 y y 21 y11 y12 y y12 g h h22 h 21 h22 1 h11 h21 h11 y12 y11 y h12 h22 1 h22 1 g11 g 21 g11 h12 h11 h h11 g h11 h12 h21 h22 y11 y12 y 22 1 y 22 h22 h h 21 h 1 y 21 y 11 y 21 h h21 h 22 h21 1 y12 y 22 y12 1 h12 h 22 h12 g 22 g 21 g 22 g 22 g g 21 g t g12 g11 g g11 g12 g 22 1 g 22 g 12 g g 22 g h12 h h11 h g11 g12 g 21 g 22 h11 h21 1 h21 1 g 21 g11 g 21 g 22 g 21 g g g 22 g12 1 g12 h11 h12 h h12 g12 g 11 g12 t11 t 21 1 t 21 t 22 t12 1 t12 s t t 21 t 22 t 21 t11 t12 t t 22 t 21 t 22 t12 t 22 1 t 22 t 21 t11 1 t11 t11 t t12 t t11 t12 t11 t12 t 21 t 22 g 21 Pag. 15 t 22 t t 21 t t12 t t11 t s 22 s 21 s s 21 1 s 21 s 11 s 21 s11 s12 s s12 1 s12 s 22 s12 s12 s11 s s11 1 s11 s 21 s11 s 21 s 22 s s 22 s 22 s s 21 s 1 s 22 s 12 s 22 s12 s s11 s s11 s12 s 21 s 22