Aumento de precios Escuela: Profesor (a): _______________________________________________________________ Plan de Clase (1/2)

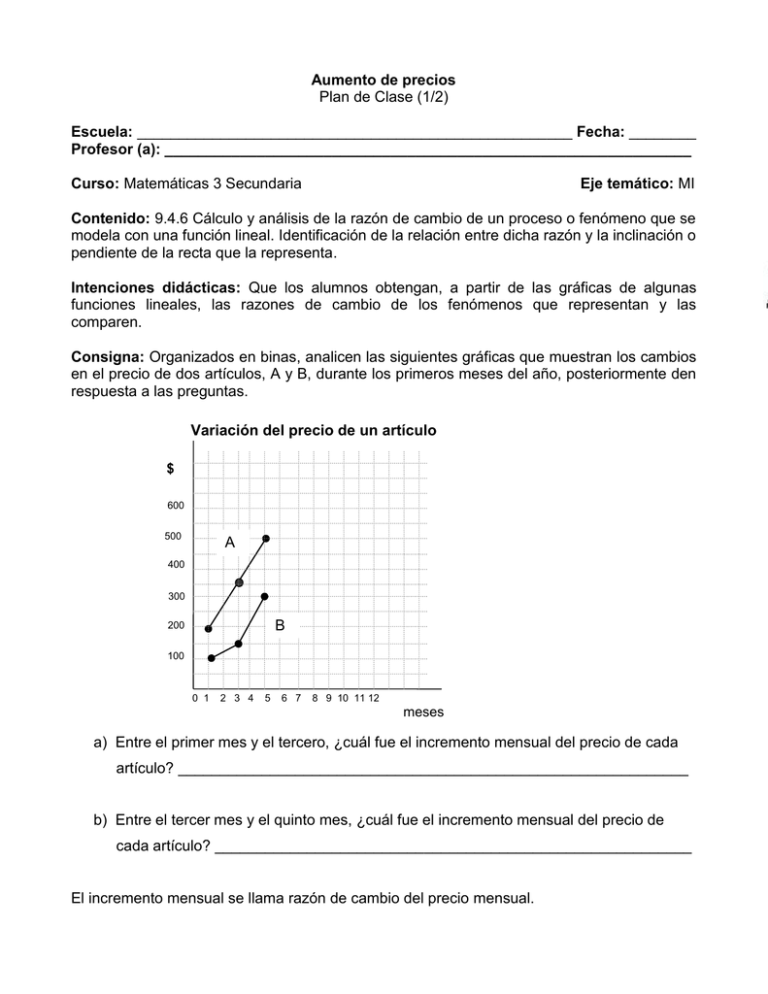
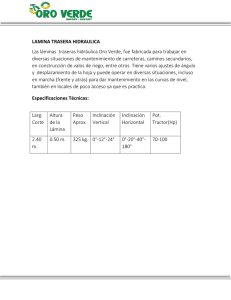
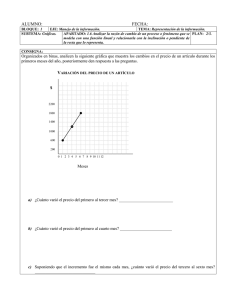
Aumento de precios
Plan de Clase (1/2)
Escuela: ____________________________________________________ Fecha: ________
Profesor (a): _______________________________________________________________
Curso: Matemáticas 3 Secundaria
Eje temático: MI
Contenido: 9.4.6 Cálculo y análisis de la razón de cambio de un proceso o fenómeno que se
modela con una función lineal. Identificación de la relación entre dicha razón y la inclinación o
pendiente de la recta que la representa.
Intenciones didácticas: Que los alumnos obtengan, a partir de las gráficas de algunas
funciones lineales, las razones de cambio de los fenómenos que representan y las
comparen.
Consigna: Organizados en binas, analicen las siguientes gráficas que muestran los cambios
en el precio de dos artículos, A y B, durante los primeros meses del año, posteriormente den
respuesta a las preguntas.
Variación del precio de un artículo
$
600
500
A
400
300
B
200
100
0 1
2 3 4
5
6 7
8 9 10 11 12
meses
a) Entre el primer mes y el tercero, ¿cuál fue el incremento mensual del precio de cada
artículo? _____________________________________________________________
b) Entre el tercer mes y el quinto mes, ¿cuál fue el incremento mensual del precio de
cada artículo? _________________________________________________________
El incremento mensual se llama razón de cambio del precio mensual.
c) ¿Para qué artículo la razón de cambio del precio mensual fue la misma en los dos
periodos? __________________________________________________________
d) ¿Qué artículo tuvo una mayor razón de cambio del precio mensual, durante el primer
período en comparación con el segundo? __________________________________
Consideraciones previas:
Es posible que los alumnos confundan el precio del artículo y el incremento del mismo, en
cuyo caso es preciso ayudarlos a distinguir dichos valores. Por ejemplo, en el tercer mes el
precio del artículo A es de $350.00 y el incremento respecto al primer mes es de $150.00.
El maestro puede hacer notar a los alumnos que las gráficas que corresponden a los dos
periodos del producto A tienen la misma inclinación (de hecho, forman una recta) mientras
que las que corresponden al producto B tienen inclinaciones distintas; así mismo, las gráficas
de los dos productos, en el segundo periodo, tienen la misma inclinación, son paralelas,
mientras que en el primero no. Indagar a qué puede deberse lo anterior podría conducir a
algunos alumnos a relacionar esta característica con el hecho de que el incremento por mes,
o razón de cambio, es la misma en unos casos y no en otros: cuando el incremento por mes
es el mismo, esto es, cuando las razones de cambios son iguales, las rectas tienen la misma
dirección.
Se recomienda que en otras ocasiones los alumnos busquen otros ejemplos de cantidades
que cambian de manera proporcional con el tiempo, y que analicen cómo la razón de cambio
permite saber cuánto aumentan o disminuyen por unidad de tiempo, por ejemplo: la distancia
recorrida cuando la velocidad es constante, el costo de una llamada de larga distancia, el
interés que se paga por un préstamo de dinero, etcétera.
Observaciones posteriores:
1. ¿Cuáles fueron los aspectos más exitosos de la sesión?
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase?
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para
usted.
Muy útil
Útil
Uso limitado
Pobre
Comparación de servicios
Plan de Clase (2/2)
Escuela: ____________________________________________________Fecha: ________
Profr. (a): _______________________________________________________________
Curso: Matemáticas 3 Secundaria
Eje temático: MI
Contenido: 9.4.6 Cálculo y análisis de la razón de cambio de un proceso o fenómeno que se
modela con una función lineal. Identificación de la relación entre dicha razón y la inclinación o
pendiente de la recta que la representa.
Intenciones didácticas: Que los alumnos relacionen diferentes razones de cambio con la
inclinación o pendiente de las rectas que las representan gráficamente.
Consigna: La siguiente gráfica muestra el costo del servicio telefónico de dos compañías,
con base en la información que proporciona, respondan lo que se pide.
Costo del servicio telefónico
Compañía B
Costo ($)
Compañía A
300
150
0
0
100
Número de llamadas
a) ¿Cuál es la razón de cambio (incremento en el costo por llamada) en cada compañía?
_____________________________________________________________________
b) ¿Cómo puede saberse, a partir de la inclinación de las rectas, cuál tiene mayor razón
de cambio?___________________________________________________________
c) Hay un número N de llamadas para el cual las dos compañías cobran lo mismo, ¿cuál
es? ____________________________________________________________
d) ¿Qué compañía conviene más si se hace un número mayor de llamadas que N?
_____________________________________________________________________
Consideraciones previas:
Si los alumnos tienen dificultades para identificar y obtener costos e incrementos, puede
proponérseles el llenado de una tabla como la siguiente para cada compañía:
Compañía A
Llamadas
Costo total ($)
Incremento ($)
0
150
0
1
151.50
1.50
10
165.00
15.00
50
100
Una vez que quede aclarado el significado de incremento o razón de cambio, se puede
plantear la siguiente pregunta:
Si la razón de cambio en la compañía A fuera la misma que en la compañía B, ¿cómo serían
las rectas que representan a ambos fenómenos? ¿Cómo serían sus pendientes (o su
inclinación)?
Observaciones posteriores:
1. ¿Cuáles fueron los aspectos más exitosos de la sesión?
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase?
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para
usted.
Muy útil
Útil
Uso limitado
Pobre
14/15