cap8partA v7 def
Anuncio
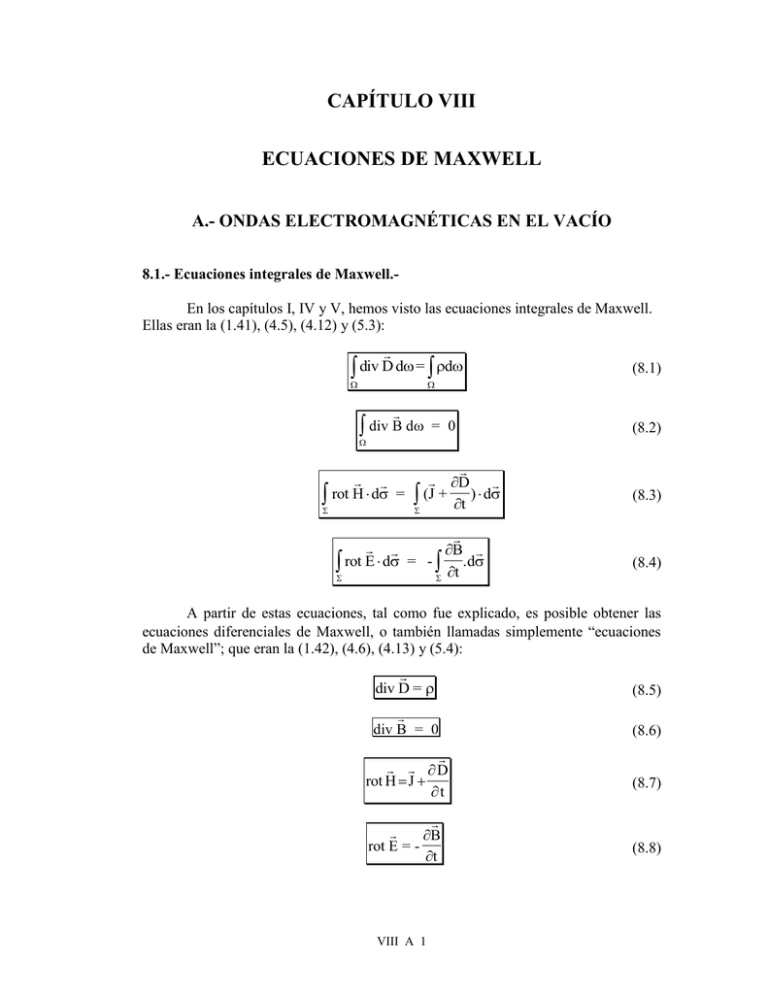
CAPÍTULO VIII ECUACIONES DE MAXWELL A.- ONDAS ELECTROMAGNÉTICAS EN EL VACÍO 8.1.- Ecuaciones integrales de Maxwell.En los capítulos I, IV y V, hemos visto las ecuaciones integrales de Maxwell. Ellas eran la (1.41), (4.5), (4.12) y (5.3): div D d = d (8.1) div B d = 0 (8.2) rot H d = D (J + t ) d B rot E d = - t .d (8.3) (8.4) A partir de estas ecuaciones, tal como fue explicado, es posible obtener las ecuaciones diferenciales de Maxwell, o también llamadas simplemente “ecuaciones de Maxwell”; que eran la (1.42), (4.6), (4.13) y (5.4): div D = (8.5) div B = 0 (8.6) D rot H J t B rot E = t VIII A 1 (8.7) (8.8) Fueron escritas por primera vez por J. C. Maxwell, en una serie de publicaciones que comenzaron hacia 1856 y concluyeron en 1864. Pueden ser consideradas como el fundamento del electromagnetismo, y se verifican en función de las consecuencias que de ellas se desprenden. El sentido físico de estas ecuaciones integrales y diferenciales también fue explicado en los capítulos ya mencionados. 8.2.- Solución de las ecuaciones de Maxwell en el vacío.Vamos a escribir las ecuaciones diferenciales de Maxwell (8.5) a (8.8) en el vacío, en el cual como se sabe, no hay cargas ni corrientes, y por lo tanto, es: = 0 ; = 0 = 0 ; J 0 Por otra parte, recordemos que: D = 0 E B = 0 H Finalmente las ecuaciones (8.5) a (8.8) las podemos escribir de la siguiente manera: div E = 0 (8.9) div H = 0 (8.10) E rot H = 0 t H rot E = - 0 t (8.11) (8.12) Vamos ahora a tratar de Observemos que estas ecuaciones tienen resolverlas. dos incógnitas vectoriales: E y H , o bien 6 incógnitas escalares, que son las componentes de esos vectores. Para encontrar la solución, seguimos a Maxwell. Si se vuelve a aplicar rotor, por ejemplo a la (8.12), se tiene: H rot rot E =- rot ( 0 ) t y reemplazando en el primer miembro el operador rot rot por uno equivalente, queda: VIII A 2 grad div E - 2 E - 0 ( rot H) t Teniendo en cuenta las ecuaciones (8.9) y (8.11), se obtiene: 2 E E 0 0 2 t 2 (8.13) que es una ecuación de ondas, también llamada ecuación de D’Alambert. En su versión para una sola variable espacial fue usada por primera vez en la solución del problema de la cuerda vibrante. Aplicando el operador rotor, esta vez a la ecuación (8.11), y operando en forma similar a la anterior, se obtiene otra ecuación de D’Alambert para H : 2 H 2 H = 0 0 2 t (8.14) Es decir, que resolver las ecuaciones (8.9) a (8.12) significa en realidad resolver las (8.13) y (8.14). Como la ecuación de D’Alambert tiene soluciones ondulatorias, estudiaremos sus características físico-matemáticas a través de sus expresiones más simples: las ondas planas. Las escribiremos de la siguiente forma: donde: = E = E 0 e j ( kr t ) (8.15) H = H 0 e j (kr - t) (8.16) 2 = 2 f T k = k x i k y j k zk r = x i + y j+zk y kx 2 2 2 ; ky ; kz ; x y z siendo es la frecuencia angular, T, el período, f, la frecuencia, k , el vector de VIII A 3 Fig. 8.1 onda, y r el vector posición. El producto escalar de estos dos últimos vectores igualado a una constante, da la ecuación de un plano, que es el plano de fase constante. (Véase la figura 8.1). Obsérvese que k es perpendicular al plano de fase constante. Por otra parte, tanto E0 comoH0 , que son las amplitudes de ambas soluciones, tienen carácter vectorial. Ello implica que las amplitudes tienen dirección y sentido, lo cual marca que son ondas vectoriales. Obviamente, las soluciones también lo son. Estamos entonces en presencia de ondas planas y polarizadas. Ello resulta de: k r = k x x k y y k z z = constante La velocidad de propagación de la fase, o velocidad de fase, se obtiene de: k r t = cte. y es: k x k y k z t cte x y z diferenciando: kx dx dy dz ky kz dt dt dt k.v y como k // v , resulta v k o, en función de la frecuencia y la longitud de onda v 2 f k T 2 VIII A 4 Además, en la ecuación general de D’Alambert, (8.17), el coeficiente v2 del segundo miembro es el cuadrado de la velocidad. Es decir, que si la escribimos en forma genérica para un vector A cualquiera, resulta: 1 2 A A = 2 2 v t 2 (8.17) y comparando con la (8.13) y la (8.14), resulta que la velocidad de propagación de las ondas electromagnéticas es: v = 1 = 0o 1 (8,85 pF / m ) (400 nH / m) = c 3 108 m s que, como se sabe, es la velocidad de la luz en el vacío. Inicialmente Maxwell, hacia 1857, tomó los valores de la constante dieléctrica y de la permeabilidad magnética del vacío de los disponibles en la época, según mediciones de Kohlrausch y Weber, y obtuvo unos 310.000 Km/s. Posteriormente, en 1907, Rosa y Dorsey volvieron a medir esas constantes y obtuvieron 299.784 10 Km/s. Pasando los años, esta constante universal fue medida por diferentes métodos, obteniéndose cada vez resultados más precisos. El valor de la velocidad de la luz actualmente aceptado es: c = 299.792.456,2 1,1 m/s 8.3.- Ondas planas, esféricas y cilíndricas.- Se dice que una onda es plana si, en cada instante, las funciones E y H tienen el mismo valor en todos los puntos de un plano perpendicular a una dirección fija, definida por el vector de propagación k . Si, en cambio, en cada instante dichas funciones tuvieran el mismo valor sobre una esfera, estaríamos en presencia de ondas esféricas, y si lo tuvieran sobre una superficie cilíndrica, serían ondas cilíndricas. Cada uno de estos tipos de onda se obtiene, por supuesto, como solución de la ecuación de ondas o de D’Alambert, y lo que define el problema es la simetría que presenta. En efecto, si la fuente es puntual, genera ondas esféricas. Si la fuente es una línea de radiación (por ejemplo una ranura en óptica), genera ondas cilíndricas. Las ondas planas se presentan cuando se está muy lejos de cualquiera de esas dos fuentes, y se toma una superficie pequeña del frente de onda. En la ecuación de D’Alambert habrá que utilizar la expresión del laplaciano correspondiente a la simetría de que se trate. En la tabla que sigue, se resume esta situación. En el caso de la simetría cilíndrica, la solución que se presenta corresponde VIII A 5 al caso en el cual el frente de onda está lejos de la fuente. En los otros dos casos las soluciones son exactas. En la tabla 8.1 hacemos un resumen de la situación arriba descripta. 8.4.- Relación entre los vectores E y H.En las ecuaciones de Maxwell en el vacío, dadas por las (8.9) a (8.12), se pueden distinguir tres operadores: el operador derivada parcial temporal, el operador rotor y el operador divergencia. Cada uno de ellos actúa sobre los vectores E y H . simetría Tabla 8.1 coord. del laplac. Coordenadas plana Cartesianas (x,y,z) esférica Esféricas (r,,) cilíndrica Cilíndricas (r,,z) Solución E = E 0e j( k r t ) E 0 j( k r t ) E= e r E E = 0 e j( kr t ) r Para encontrar la relación entre ellos, aplicaremos las soluciones encontradas para las ecuaciones de D’Alambert, (8.15) y (8.16) a las ecuaciones de Maxwell. Por ejemplo, hagamos: j( k r t ) E = -jE 0 e = -jE t y aplicando los operadores divergencia y rotor, se obtiene (dejamos la demostración como ejercicio para el lector): div E = jk E rot E = jk E El mismo tipo de resultado se obtiene cuando se aplican dichos operadores al vector H , solución de la ecuación de D’Alambert respectiva. Escribiendo ahora las ecuaciones de Maxwell en el vacío (8.9) a (8.12), de la forma arriba mostrada, simplificando las j y ordenando, se obtiene: k E = 0 (8.18) k H = 0 (8.19) VIII A 6 k H = -0E (8.20) k E = 0H (8.21) De estas ecuaciones es fácil ver que si: kE =0 kH =0 k E k H y además, teniendo en cuenta la (8.20) y la (8.21), se deduce que: EH lo que muestra que son ondas transversales, pues es perpendicular k a E y H , y éstos son perpendiculares entre sí, como se muestra en la figura 8.2. Además, si en la (8.21) tomamos módulo, se obtiene: 0 E = = H k o = 0 = 120 0 valor que se conoce con el nombre de impedancia característica del vacío. (Las unidades son compatibles, ya que E se mide en V/m y H en A/m). Fig. 8.2 Una relación muy útil es: 0 E = o H (8.22) Hemos visto, entonces, que el vector intensidad de campo eléctrico es perpendicular al vector intensidad de campo magnético, y que por lo tanto las ondas vectoriales se propagan perpendicularmente entre sí. Se puede apreciar que estas ondas vectoriales son transversales, ya que no existen componentes de campo eléctrico o magnético en la dirección de la propagación. Además, en el vacío, la relación entre los vectores es la impedancia característica del vacío, y se propagan a la velocidad de la luz. VIII A 7