Cálculo de varias variables
Anuncio
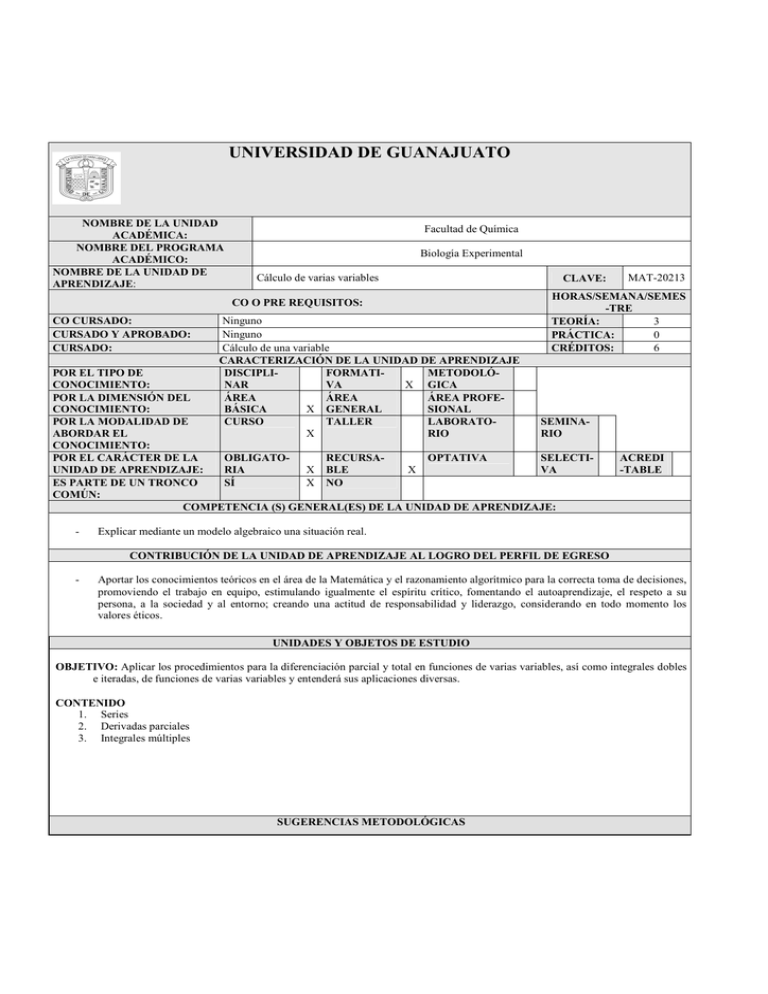
UNIVERSIDAD DE GUANAJUATO NOMBRE DE LA UNIDAD ACADÉMICA: NOMBRE DEL PROGRAMA ACADÉMICO: NOMBRE DE LA UNIDAD DE APRENDIZAJE: Facultad de Química Biología Experimental Cálculo de varias variables CO O PRE REQUISITOS: CO CURSADO: CURSADO Y APROBADO: CURSADO: Ninguno Ninguno Cálculo de una variable CARACTERIZACIÓN DE LA UNIDAD DE APRENDIZAJE DISCIPLIFORMATIMETODOLÓX GICA NAR VA ÁREA ÁREA ÁREA PROFEX GENERAL BÁSICA SIONAL CURSO TALLER LABORATOX RIO CLAVE: HORAS/SEMANA/SEMES -TRE 3 TEORÍA: 0 PRÁCTICA: 6 CRÉDITOS: POR EL TIPO DE CONOCIMIENTO: POR LA DIMENSIÓN DEL CONOCIMIENTO: POR LA MODALIDAD DE SEMINAABORDAR EL RIO CONOCIMIENTO: POR EL CARÁCTER DE LA OBLIGATORECURSAOPTATIVA SELECTIX BLE X UNIDAD DE APRENDIZAJE: RIA VA X NO ES PARTE DE UN TRONCO SÍ COMÚN: COMPETENCIA (S) GENERAL(ES) DE LA UNIDAD DE APRENDIZAJE: - MAT-20213 ACREDI -TABLE Explicar mediante un modelo algebraico una situación real. CONTRIBUCIÓN DE LA UNIDAD DE APRENDIZAJE AL LOGRO DEL PERFIL DE EGRESO - Aportar los conocimientos teóricos en el área de la Matemática y el razonamiento algorítmico para la correcta toma de decisiones, promoviendo el trabajo en equipo, estimulando igualmente el espíritu crítico, fomentando el autoaprendizaje, el respeto a su persona, a la sociedad y al entorno; creando una actitud de responsabilidad y liderazgo, considerando en todo momento los valores éticos. UNIDADES Y OBJETOS DE ESTUDIO OBJETIVO: Aplicar los procedimientos para la diferenciación parcial y total en funciones de varias variables, así como integrales dobles e iteradas, de funciones de varias variables y entenderá sus aplicaciones diversas. CONTENIDO 1. Series 2. Derivadas parciales 3. Integrales múltiples SUGERENCIAS METODOLÓGICAS - - - 1. 2. 3. Por el contenido de los temas que son abordados en el curso de cálculo de varias variables, se hace necesario el utilizar las herramientas computacionales y de bibliografía correspondientes, en los que se pueda describir una función de varias variables que deberán mostrarse a los alumnos. El coordinador del curso expondrá en clase alguna metodología correspondiente para la aplicación de las técnicas correspondientes para los temas que se analizarán, en el que se explicará las deducciones de las fórmulas a aplicar y a realizar ejercicios para la aplicación de las mismas. El coordinador del curso dejará temas para exposición de los alumnos, en los que se considere la explicación de una deducción para un tema por ver o la aplicación a problemas diversos. Durante el transcurso del semestre se plantearán tareas para que el alumno desarrolle como actividad extraclase y se procurará comentar las dudas pertinentes para completar el aprendizaje del estudiante. Se elaborarán tres exámenes parciales, en el que se contemplarán los temas de las tres unidades que se especifican en el programa para la materia. SUGERENCIAS PARA LA EVALUACIÓN DEL APRENDIZAJE Evaluación: Se puede hacer una evaluación diagnóstica para la valoración de los conocimientos previos de los estudiantes. Para la evaluación del curso, serán contemplados los exámenes parciales que se referirán a los temas que fueron vistos para evaluación, será también importante considerar las tareas, la participación individual de los alumnos así como la investigación que realicen para la explicación de un tema a abordar. De todo esto deberá llevarse un control del desempeño de los estudiantes. La evaluación sumativa, en el cuál se establecen los trabajos finales del curso, y tiene como finalidad valorar el proceso de aprendizaje y asignar la calificación final de la materia. Calificación: 1. Primer parcial (integrales propias.- formas indeterminadas) (20%); 2. Segundo parcial (derivación parcial) (25%); 3. Tercer parcial (integrales múltiples) (30%); 4. Tareas correspondientes a todo el curso (10%); 5. partición individual (5%); 6. participación en equipo (10%). Acreditación: Es recomendable que el alumno cumpla con el 85% como mínimo, de las asistencias al curso. Que el alumno muestre su buen desempeño y constancia en tareas, participaciones y que apruebe los exámenes parciales, para que la calificación final sea aprobatoria. 1. 2. 3. 4. 5. BIBLIOGRAFÍA BÁSICA Leithold Louis. El Cálculo. Oxford University Press, 7ª edición, México,1998 Purcell, Edwin J.Y Varberg, Dale. Cálculo con geometría analítica. Prentice Hall. Cuarta edición. México, 1987 Stein, Srerman K.y Barcellos Anthony. Cálculo y geometría analítica. Mc Graw Hill. Quinta edición. México, 1995 Stewart, James. Cálculo. Grupo editorial Iberoamericana, segunda edición. México,1994 Zill, Dennis G. Ecuaciones diferenciales. Grupo Editorial Iberoamericana. 1. 2. 3. 4. 5. BIBLIOGRAFÍA COMPLEMENTARIA Goodman. A. W. Geometría analítica y cálculo. Uteha. Primera edición. México, 1980. L. Salas, C.G. Salas. Curso de preparación para cálculo. Editorial Limusa, primera edición. México, 1982 Swokowski, Earl W. El cálculo con geometría analítica. Grupo Editorial Iberoamericana. Segunda edición. México, 1989 Zill, Dennis G. Calculo con geometría analítica. Grupo Editorial Iberoamericana, primera edición. México, 1987. Courant R., John F. Introducción al cálculo y al análisis matemático.- Vol. II.- Editorial Limusa. México 1979. ELABORADA POR: Comisión de Tronco Común y profesores invitados FECHA DE ELABORACIÓN: 15 de octubre de 2007 FECHA DE REVISIÓN