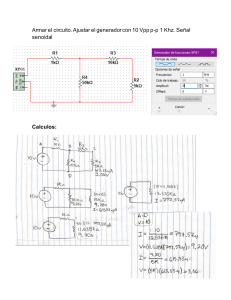
Objetivo de la Práctica •

• Objetivo de la Práctica
El objetivo de la práctica es el conocimiento y manejo del osciloscopio, así como la utilización del polímetro
para medidas de resistencias, corrientes y voltajes. Asimismo, se busca poner en práctica la teoría de
tratamiento de datos.
• Material Empleado
• Polímetro digital
• Pila de 4,5 V
• Tres resistencias
• Condensador
• Placa de montaje
• Cables de conexión
• Osciloscopio
• Transformador
• Fuente de alimentación
• Generador de funciones
• Método Experimental
• Utilización del polímetro como voltímetro, ohmímetro y amperímetro
• Medidas Directas
• Utilizar el polímetro para medir la tensión de la pila. Comparar los resultados obtenidos con los nominales
de la pila.
Tensión nominal de la pila: V = 4,5 V
Resultados obtenidos tras medir la tensión de la pila con el polímetro:
V------1 = 4,23 ± 0,01 V
V2 = 4,2 ± 0,1 V
• Montar un circuito como el de la figura, colocando el polímetro en serie para medir el valor de la corriente,
y en paralelo para medir la caída de tensión entre los extremos de la resistencia. Aplicando la Ley de Ohm,
V = I R, comprobar el valor de la corriente medida.
Ley de Ohm: V = I R
De esta igualdad, se obtienen los valores de las corrientes: R = V / I
Para obtener los valores de los errores de las corrientes, emplearemos el método del logaritmo neperiano:
1
R=V/I
ln R = ln (V / I) = ln V − ln I
dR / R = dV / V − dI / I
R/R=V/V−I/I
R/R=V/V+I/I
R = (V / V + I / I) R
Se han tomado datos para tres resistencias distintas, donde el valor nominal de cada una se obtiene a partir de
esta igualdad:
R = ab · 10c.
El valor de cada color es el siguiente:
Color
Negro
Marrón
Rojo
Naranja
Amarillo
Verde
Azul
Violeta
Gris
Blanco
Valor
0
1
2
3
4
5
6
7
8
9
Resultados obtenidos:
Resistencias
R±1
a = azul; b = gris;
c = negro.
Intensidad de
corriente
Tensión
Resistencia
Error R
R±R
V ± 0,01 V
R=V/I
53,3
3,58
67,1669
0,3136
67,2 ± 0,3
4,1
4,08
995,1219
26,7103
1000 ± 30
86,7
3,24
37,3702
0,1584
37,37 ± 0,16
I ± 0,1 mA
R1 = 68 · 100 = 68
a = marrón; b = negro;
c = rojo.
R2 = 10 · 102 = 1000
a = naranja; b = blanco;
2
c = negro.
R3 = 39 · 100 = 39
En el error de la medida, aparte del error de precisión, p, también hay que tener en cuenta los errores
sistemáticos debidos al posible mal funcionamiento o calibración de los equipos de medida.
• Medidas Indirectas. Resistencia Equivalente de un Conjunto de Resistencias
• Utilizando la pila medida en el apartado anterior, medir la corriente del circuito. Aplicando la Ley de Ohm,
calcular el valor de la resistencia equivalente del conjunto de las dos resistencias asociadas en serie y en
paralelo.
i. Comprobar que la asociación en serie de resistencias verifica:
Req = R1 + R2
ii. Comprobar que la asociación de resistencias en paralelo cumple la siguiente igualdad:
1 / Req = 1 / R1 + 1 / Req
R=V/I
Los errores de las medidas de las resistencias se obtienen por el método de las derivadas parciales:
R = ø"R / "VøV + ø"R / "IøI
"R / "V = V / I
"R / "I = −V I / I2
Tipo de circuito
Intensidad
Caída de
de
tensión:
corriente:
A ± 0,1
mA
V ± 0,01
V
Resistencias en serie:
R=V/I
R±R
Resistencia
Teórica
R = 1053,846
3,9
4,11
R = 27,0217
R1 = 1000
R = 1050 ± 30
R2 = 39
R = R1 + R2
R = 1039
3
Resistencias en paralelo:
R1 = 68
R = 62,9432
56,4
3,55
R = 0,1121
R = 62,94 ±
0,11
R2 = 1000
R−1 =
(R1)−1 +
(R2)−1
R = 63,6704
Como puede observarse, los distintos circuitos cumplen perfectamente la ley de Ohm. Esto es, conectando
cualquier tipo de resistencia, sea en paralelo sea en serie, se obtienen unos resultados muy parecidos a los
teóricos. Es más, las relaciones entre resistencias se cumplen, ya que los resultados experimentales se
aproximan bastante a los teóricos.
• Utilización del Osciloscopio: Medida y Comparación de Señales
• Utilizar el osciloscopio para medir la tensión de la pila.
V = 4,2 ± 0,1 V
• Utilizar el osciloscopio para medir la tensión pico a pico, Vpp, de las diferentes salidas del transformador
conectado a la red. Obtener los valores eficaces. Medir el período de oscilación de la señal de la red y
obtener su frecuencia. ¿Es el valor esperado?
Vpp = 2 V0
V(t) = V0 sin ( t)
4
V0 = Vpp / 2
=2
Vef = V0 / (2)1/2 = Vpp / 2 (2)1/2
Por el método del neperiano hallamos el error de Vef :
Vef = (Vpp / Vpp ) Vef
Valores eficaces,
Salidas del transformador
Tensión pico a
pico, Vpp
Tensión T, s
Vef = Vpp / 2
(2)1/2
Vpp ± 0,1 V
Frecuencia ,
s−1
Vef ± Vef V
10,6066
T = 20 · 10−3 s
6 · 5 = 30 V
0,03535
= 50 s−1 (Hz)
10,61 ± 0,04 V
7,0711
T = 20 · 10−3 s
4 · 5 = 20 V
0,03535
= 50 s−1 (Hz)
7,07 ± 0,04 V
7,0711
T = 20 · 10−3 s
4 · 5 = 20 V
0,03535
= 50 s−1 (Hz)
7,07 ± 0,04 V
7,0711
T = 20 · 10−3 s
4 · 5 = 20 V
0,03535
= 50 s−1 (Hz)
7,07 ± 0,04 V
• También se puede conocer la frecuencia de una señal utilizando un generador de frecuencias.
Generando una frecuencia = 1 KHz:
Vpp = 4· 5 = 20 V
V0 = Vpp / 2 = 10 V
Vef = V0 / 21/2 = 7,07 V
T = 10 · 0,1 ms = 10−3 s
= 1 / T = 103 s−1 = 103 Hz = 1 KHz, que es el valor que realmente se ha generado.
5