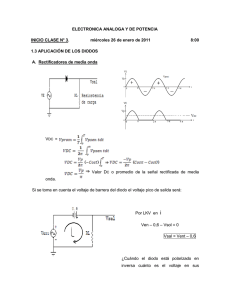
Voltaje de Rizo en Filtros RC

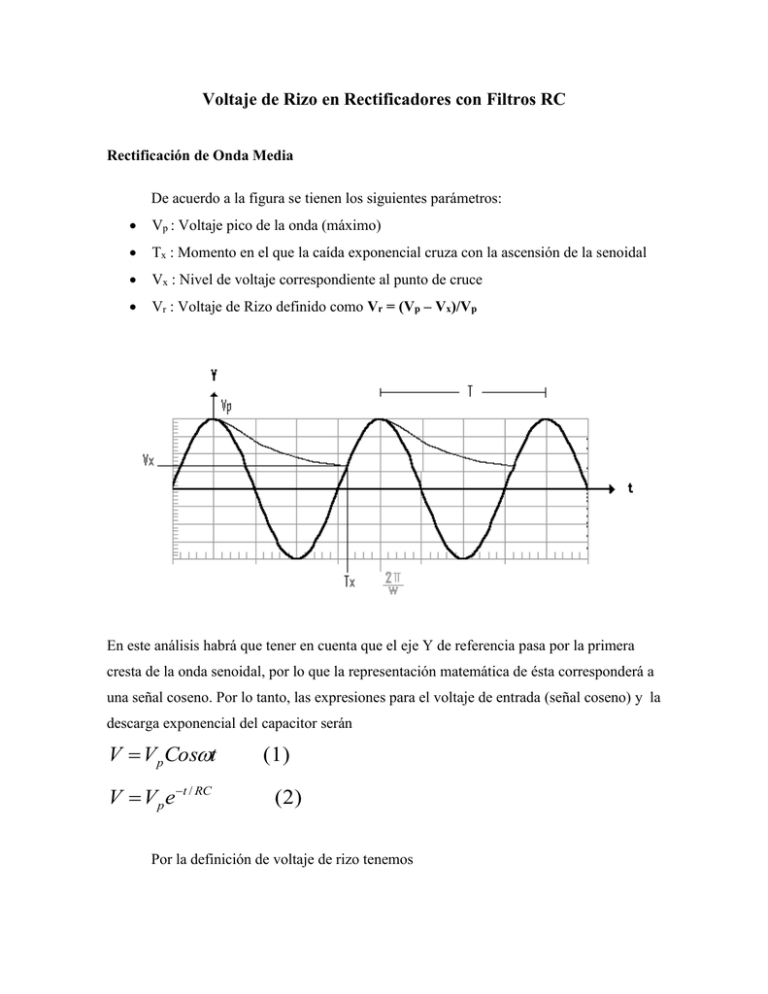
Voltaje de Rizo en Rectificadores con Filtros RC
Rectificación de Onda Media
De acuerdo a la figura se tienen los siguientes parámetros:

Vp : Voltaje pico de la onda (máximo)

Tx : Momento en el que la caída exponencial cruza con la ascensión de la senoidal

Vx : Nivel de voltaje correspondiente al punto de cruce

Vr : Voltaje de Rizo definido como Vr = (Vp – Vx)/Vp
En este análisis habrá que tener en cuenta que el eje Y de referencia pasa por la primera
cresta de la onda senoidal, por lo que la representación matemática de ésta corresponderá a
una señal coseno. Por lo tanto, las expresiones para el voltaje de entrada (señal coseno) y la
descarga exponencial del capacitor serán
V  Vp Cost
V  Vp et / RC
(1)
(2)
Por la definición de voltaje de rizo tenemos
Vr  (V p  Vx ) / V p
(3)
Ahora bien, la señal exponencial se encuentra (cruza) con la cosenoidal en el punto tx,Vx
por lo que se tiene
VpCost x  Vpetx / RC  Vx
(4)
El problema de esta ecuación es que no se puede resolver para tx que es la variable que nos
interesa. Así que mejor damos un pequeño rodeo en la siguiente forma. Despejamos Vx de
la ecuación (3)
Vx  (1  Vr )V p
(5)
Igualando (5) con el miembro derecho de (4)
Vpetx / RC  (1 Vr )Vp
De donde se obtiene
t x  RC ln(1  Vr )
(6)
En forma similar, al igualar (5) con el miembro izquierdo de (4)
V p Cost x  (1  Vr )V p
Por lo tanto
tx 
1

Cos 1 (1  Vr )
(7)
Aunque la expresión anterior es matemáticamente correcta, los valores de tx que la
satisfacen son infinitos ya la función coseno se repite periódicamente. Debemos limitar el
valor de tx al que se refiere la gráfica de la descarga del capacitor. Esto es, el valor correcto
de tx es el que se localiza entre
3
2
 tx 
2

Por lo tanto, el valor de tx es
tx 
2


1

Cos 1 (1  Vr )
Al igualar con 6 y despejar queda
(8)
2  Cos1 (1  Vr )
RC 
 ln(1  Vr )
(9)
Esta ecuación nos permite calcular el valor de la capacitancia para cualquier voltaje de rizo
y resistencia de carga.
Procediendo en forma similar se puede demostrar que la correspondiente relación para un
rectificador de onda completa es
Cos1 (Vr  1)
RC 
  ln(1  Vr )
(10)