Modelo de prueba 1.

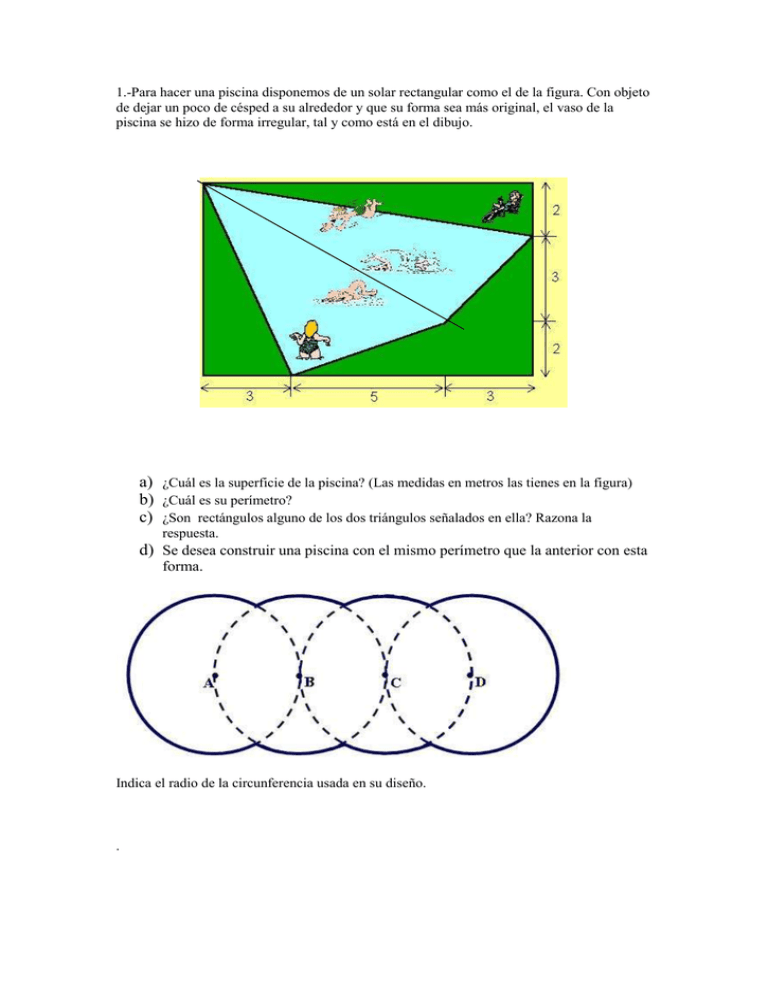
1.-Para hacer una piscina disponemos de un solar rectangular como el de la figura. Con objeto
de dejar un poco de césped a su alrededor y que su forma sea más original, el vaso de la
piscina se hizo de forma irregular, tal y como está en el dibujo.
a) ¿Cuál es la superficie de la piscina? (Las medidas en metros las tienes en la figura)
b) ¿Cuál es su perímetro?
c) ¿Son rectángulos alguno de los dos triángulos señalados en ella? Razona la
respuesta.
d) Se desea construir una piscina con el mismo perímetro que la anterior con esta
forma.
Indica el radio de la circunferencia usada en su diseño.
.
2.a) Ampliando: Calcula x e y (1’25 ptos)
y
5 cm
125%
12 cm
x cm
3.- El lado del cuadrado ABCD mide 1 dm.
a)Identifica en la siguiente figura , si existen, un sector circular , un trapecio circular, una
corona circular y un segmento circular.
b)Considera otra circunferencia de radio 23 cm. ¿A qué distancia deben estar los
centros de esta circunferencia y la que pasa por los puntos A,B,C y D para que sean
tangentes interiores?
c)En una circunferencia la longitud de una de sus cuerdas es de 48 cm .Esta cuerda dista 7
cm del centro.
a)Calcular el área del círculo definido por dicha circunferencia.
b)Determina el ángulo definido por los dos radios que unen el centro de la circunferencia con
los extremos de la cuerda.
c) Calcula el área y el perímetro del segmento circular limitado por la circunferencia y esa
cuerda.
4.- Calcula el valor de los ángulos de este triángulo.Observa que todos los vértices del mismo
están situados sobre puntos de una misma circunferencia.
5.- Calcula la superficie de la zona no coloreada.
6.-Resuelve el siguiente sistema por sustitución.
7 .-Este sistema tiene una única solución. Demuestra esta afirmación sin resolver el sistema
¿Por qué valor habría que cambiar el coeficiente 5 de la segunda ecuación para que el sistema
no tuviera solución?
8.- Usando el compás , marca la zona a la que puede acceder un perro atado en el vértice A
suponiendo que la longitud de su correa es la dada por este segmento.
4 metros
3 metros
A
La figura no
está
representada a
tamaño real
5 metros
Calcula el perímetro y el área de la zona a la que tiene acceso el perro
9.- a)
Si el área de la figura representada fuera 10 centímetros cuadrados, ¿cuál sería el área de la
figura obtenida al hacer en una fotocopiadora una ampliación del 120%?
b) Indica si son semejantes o no las siguientes parejas de triángulos. En el caso de que lo sean
calcula la razón de semejanza.
-Los tres lados del triángulo 1 miden 3,7 y 9 y los del triángulo 2 miden 4,12 y 28/3.
-Tengo dos triángulos isósceles .En uno de ellos el ángulo desigual mide 40º. En el
otro uno de los ángulos iguales mide 70º . El lado desigual mide 3 cm. en el primero y
5 cm. en el segundo.
-Dos lados de un triángulo rectángulo son el doble de largos que sus correspondientes
en otro triángulo no rectángulo.
10.-Completa: (8 puntos)
Un polígono regular tiene 90 diagonales. Por tanto su número de lados es _____, su ángulo
central mide_____ y sus ángulos interiores valen_______.
Un polígono regular tiene como medida de sus ángulos interiores 150º. Por tanto tiene _____
lados, su ángulo central vale____ y sus diagonales son un total de _____.
11.- Tenemos un triángulo equilátero de lado igual a 20 cm. En él hemos trazado sus tres
alturas y sombreado un cuadrilátero definida por ellas.
a) ¿Cuánto mide cada altura? ( 3 puntos)
b) Indica qué tipo de cuadrilátero es el sombreado en el interior del cuadrilátero.( 2
puntos)
c) ¿Qué carácterísticas tienen las diagonales de ese cuadrilátero? (2 puntos)
d) Completa: (4 puntos)
a. Una de las diagonales del cuadrilátero señalado lo divide en dos triángulos
_________________ desiguales ya que uno es ___________ y el otro es
_____________.
b. La otra diagonal divide ese cuadrilátero en dos triángulos _______________
iguales.
12.- Determina el perímetro de este trapecio isósceles de altura igual a 7 cm (7 puntos)
8
3
13.-En un ciber-café la cuota para acceder a una conexión a Internet es de 1 € . Por cada minuto que
estemos durante la primera hora nos cobran 0,05 € y en las siguientes la mitad ,es decir 0,025€.
Representa gráficamente en los ejes abajo indicados cómo varía el coste del acceso a Internet en € (y)
con el tiempo en horas (x). No modifiques la escala indicada. (1 pto)
¿Cuánto tiempo habré estado conectado si me han cobrado 16 euros? (0’5 ptos)
14.-Observa las siguientes gráficas y las informaciones que las acompañan. En las gráficas se
representa el coste de una llamada en céntimos de Euro (eje y) y su duración en minutos (eje
x) .Cada una de ellas corresponde a una compañía diferente.
Compañía 1
3
Compañía 2
Compañía
10
Coste por minuto :0’05 €
Coste por minuto :0’07 €
5
Una llamada de 15 minutos
cuesta 1’20 €
a) Observando las gráficas comenta las características de las ofertas realizadas por las
tres compañías.
b) Rellena las siguientes tablas para cada una de las compañías:
Compañía 1
Tiempo(mn) 0
Coste (€)
1
2
3
4
5
20
40
Compañía 2
Tiempo(mn) 0
Coste (€)
1
2
3
4
5
20
40
Compañía 3
Tiempo(mn) 0
Coste (€)
1
2
3
4
5
20
40
c) Escribe la expresión algebraica asociada a la gráfica de cada compañía. Recuerda que
esas gráficas corresponden a funciones afines.
Compañía 1
Y=
Compañía 2
Y=
Compañía 3
Y=
d) Representa en los siguientes ejes de forma simultánea las gráficas de las tres
compañías. 1)Hazlo de la forma más exacta que puedas.2)Selecciona una escala
adecuada para los ejes y 3) usa un color distinto para cada gráfica.
e) ¿Cuál es la mejor oferta si …
a. …deseo hacer una llamada de 4 minutos?
b. …deseo hacer una llamada de 10 minutos?
c. …deseo hacer una llamada de 25 minutos?
d. …deseo hacer una llamada de 55 minutos?
f) ¿Para qué duración de llamadas es más interesante…
…la oferta de la compañía 1?
…la oferta de la compañía 2?
…la oferta de la compañía 3?
g) Una cuarta compañía nos cobra por una llamada de 20 minutos 1’8 Euros, y por una
llamada de 30 minutos 2’50, sabiendo que la función que relaciona tiempo con coste
es afin, determina su expresión algebraica e interpreta el significado de sus
parámetros.
h) ¿Cuánto costará una llamada de 50 minutos en esta última compañía?
15.a)Calcula el área de la zona coloreada en la primera figura.
b)Calcula el perímetro del polígono de la segunda figura.
16.a)¿Por qué estos dos triángulos rectángulos son semejantes? (0’5 ptos)
b) Comprueba que sus lados son proporcionales.(0’5 ptos)
c)¿Cuál es la razón de semejanza de las dos figuras? (0’5 ptos)
d) Obtén dos triángulos semejantes a los mostrados. (0’5 ptos.)
17.Las bases de un trapecio isósceles miden 7 y 4 metros; su altura mide 5 metros.
b) Halla su perímetro.
PISTA:¿Cuánto mide este trozo?
7m
A
A
5m
B
4m
18.Dibuja la gráfica de las siguientes rectas:
a) pendiente = 1 y pasa por el punto (3,5).(1 punto)
b) Pendiente =-1/2 y pasa por el punto (2,-3). (1 punto)
c) Pendiente=0 y pasa por el punto (2,2). (1 punto)
B
Escribe la ecuación de cada una de ellas. (1 pto).
19.-Indica brevemente porqué no son semejantes estas dos figuras
Dibuja un triángulo semejante a éste usando el método de Thales.
20.
a)Un cuadrado de lado 3 cm. impreso en un papel se amplía mediante una fotocopia. Si la
ampliación es de un 180%, indica cuál es el área de la figura ampliada.
b)Rellena los huecos, relativos a las longitudes de los segmentos más próximos a ello, con
valores que resulten adecuados según lo que indica el teorema de Tales.
21.- ¿Cuánto suman los ángulos interiores de un polígono con 35 diagonales? (1 pto)
En la primera circunferencia dibuja una cuerda, un ángulo central, un ángulo interior y otro
inscrito. En la segunda dibuja un sector circular, un segmento circular y un trapecio circular.
(1’5 ptos)
22.- Un camión sale de una ciudad a una velocidad de 40 km/h. Una hora más tarde
sale de la misma ciudad y en la misma dirección y sentido un coche a 60 km/h.
a)Representa en un gráfico espacio(eje Y)-tiempo(eje X) el movimiento del camión.
Representa en el mismo gráfico el movimiento del coche. (1 puntos)
b)Calcula la expresión algebraica correspondiente a cada uno de esos dos gráficos.(1 punto)
c)Determina numéricamente el lugar y el momento en el que el amión es alcanzado
por el coche.(1 punto)
23.- Resuelve el siguiente sistema por el método de reducción.( 1’5 puntos)
24.- Dibuja las siguientes rectas en los ejes.(2 puntos)
a)recta de pendiente 3 que pasa por (2,1)
b) recta paralela a x-1=y que pasa por (3,6)
APLICACIONES FUNCIONES AFINES.
a) Representación del movimiento de un automóvil que circula a velocidad
constante. Relación entre el tiempo desde el comienzo del movimiento(x) y la
distancia recorrida (y)
VEHÍCULO 1: se mueve en sentido N-S a una velocidad de 60 Km/h.
VEHÍCULO 2: se mueve en sentido N-s a una velocidad de 80 km/h.
VEHÍCULO 3: se mueve en sentido N-S a una velocidad de 80 Km/h.
VEHÍCULO 4: se mueve en sentido N-S a una velocidad de 60 km/h.
Sale 100 km más al Sur del vehículo 3 al mismo tiempo que lo hace
éste.
VEHÍCULO 5: se mueve en sentido N-S a una velocidad de 60 Km/h.
VEHÍCULO 6: se mueve en sentido N-S a una velocidad de 80 km/h.
Sale del mismo sitio que el vehículo 5 pero dos horas más tarde.
VEHÍCULO 7: se mueve en sentido N-S a una velocidad de 60 Km/h.
VEHÍCULO 8: se mueve en sentido S-N a una velocidad de 80 km/h.
Sale 500 Km al Sur del vehículo 7 al mismo tiempo.
b) Rellenado de recipientes con forma de prisma cuadrado. Relación entre
volumen vertido (x) y altura alcanzada por el líquido (y).
RECIPIENTE 1: Lado de la base 3 cm.
RECIPIENTE 2: lado de la base 5 cm.
RECIPIENTE 3: lado de la base 10 cm.
c) Transformación de unidades. (Relación Euro-Dólar y relación ºC-ºF)
d) Revoluciones del motor. Representa para cada marcha la relación entre
x=velocidad (km/h) e y= revoluciones del motor (rpm)
Por cada incremento de velocidad en 1 km/h las revoluciones aumentan…
de 150 en 150 si se va en primera, de 100 en 100 si se va en segunda
de 70 en 70 si se va en tercera, de 40 en 40 si se va en cuarta y de 15
en 15 si se va en quinta.
e) Alquiler de coches:
OPCIÓN 1: Coste fijo: 80 € sin límite de kilómetros.
OPCIÓN 2: Coste fijo: 20€ + 0,20 € por kilómetro.
OPCIÓN 3: Sin coste fijo. 0,75 € por Kilómetro.
Relación entre distancia recorrida (x) y coste del alquiler (y). Indicar cuándo
interesa aceptar cada tipo de alquiler.
PARA PONERSE A PRUEBA:
1.-A.-Un hortelano ataba los manojos de espárragos con cuerdas de 20 cm de longitud y los
vendía a 3 €. Otro hortelano utilizaba un cordel de doble longitud y vendía los manojos a 6 €.
Ambos tienen la misma producción de espárragos, ¿quién ganó más dinero? Justifica.
B.-Encuentra la longitud de la trayectoria curvilínea marcada continuamente en grueso.
Los círculos tienen los centros en A, B, C y D. El radio de los cuatro círculos es de 5
cm.
2a) ¿Por qué este triángulo es rectángulo?
b) Calcula el valor de todos los ángulos de este triángulo usando exclusivamente los puntos de
la trama circular.
c)Da razones que justifiquen porqué son isósceles los dos triángulos incluidos en el triángulo
verde .
d)Calcula, sin usar el transportador, el valor de los ángulos de estos triángulos isósceles.
3.En un folio de papel están dibujados dos triángulos rectángulos .El más grande de ellos no
aparece completo.
a) Si el área del triángulo grande es 70, ¿Cuál es el valor de x?
x
7 cm
5 cm
b) calcula la medida de la hipotenusa del triángulo grande.
c) f) En una fotocopiadora quiero obtener una figura con un área igual a 2,5 veces del que tiene la
original.¿Qué ampliación debo programar?
4.-Para hacer una piscina disponemos de un solar rectangular como el de la figura. Con objeto
de dejar un poco de césped, el vaso de la piscina se hizo de forma irregular como en el dibujo.
a)¿Cuánto vale la suma de los ángulos interiores definidos en los vértices de la piscina?
b)¿De qué tipos son los triángulos que quedan a uno y a otro lado de la línea discontinua? .
Justifica la respuesta.
c) Otra piscina es un polígono regular con 65 diagonales.¿Cuál será su número de
lados?.¿cuánto medirá su ángulo central?¿Cuánto medirá cada ángulo interior?
5.-Como sabes, una de las piezas del Tangram es un cuadrado. Supongamos que, tal y
como indica la siguiente figura, su lado mide 2 cm. Determina a partir de este dato el
perímetro de la pieza que tiene forma de paralelogramo y no es un cuadrado.
6.- Calcula el valor de todos los ángulos de este triángulo sin utilizar el transportador.
Observa que sus vértices están situados sobre puntos de una misma circunferencia. (2 ptos)
7.-Un ortoedro de base cuadrada tiene un área total de 80 centímetros cuadrados. Sabiendo
que el lado de la base es de 2 cm. Calcula:
-Su altura.
-Su volumen.
-La longitud de la diagonal del ortoedro.
-
8.- Cortamos una pirámide de base cuadrada paralelamente a la base y a una distancia de 4 cm
del vértice. La altura de la pirámide y la arista de la base son 12 cm y 4 cm respectivamente.
Calcula las dimensiones de la sección obtenida.
9.-Indica si son semejantes o no las siguientes parejas de triángulos. En el caso de que lo sean
calcula la razón de semejanza. (0’75 ptos)
a)Los tres lados del triángulo 1 miden 3,7 y 9 y los del triángulo 2 miden 4,7 y 3.
b)Tengo dos triángulos rectángulos .En uno de ellos la hipotenusa mide 6 cm y un
ángulo agudo mide 35º .En el otro uno de los ángulos agudos mide 55º y la
hipotenusa vale 8 cm.
c)Dos lados de un triángulo y los correspondientes del otro son iguales.