Polarización lineal de la luz

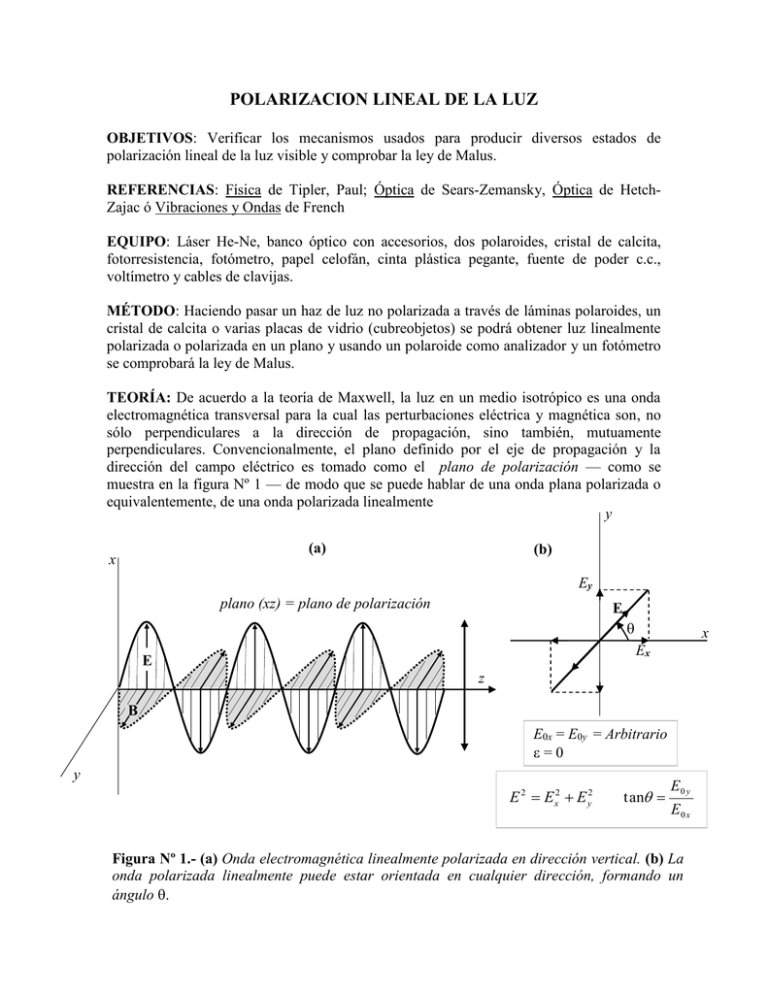
POLARIZACION LINEAL DE LA LUZ
OBJETIVOS: Verificar los mecanismos usados para producir diversos estados de
polarización lineal de la luz visible y comprobar la ley de Malus.
REFERENCIAS: Física de Tipler, Paul; Óptica de Sears-Zemansky, Óptica de HetchZajac ó Vibraciones y Ondas de French
EQUIPO: Láser He-Ne, banco óptico con accesorios, dos polaroides, cristal de calcita,
fotorresistencia, fotómetro, papel celofán, cinta plástica pegante, fuente de poder c.c.,
voltímetro y cables de clavijas.
MÉTODO: Haciendo pasar un haz de luz no polarizada a través de láminas polaroides, un
cristal de calcita o varias placas de vidrio (cubreobjetos) se podrá obtener luz linealmente
polarizada o polarizada en un plano y usando un polaroide como analizador y un fotómetro
se comprobará la ley de Malus.
TEORÍA: De acuerdo a la teoría de Maxwell, la luz en un medio isotrópico es una onda
electromagnética transversal para la cual las perturbaciones eléctrica y magnética son, no
sólo perpendiculares a la dirección de propagación, sino también, mutuamente
perpendiculares. Convencionalmente, el plano definido por el eje de propagación y la
dirección del campo eléctrico es tomado como el plano de polarización — como se
muestra en la figura Nº 1 — de modo que se puede hablar de una onda plana polarizada o
equivalentemente, de una onda polarizada linealmente
y
(a)
x
(b)
Ey
plano (xz) = plano de polarización
E

x
Ex
E
z
B
E0x = E0y = Arbitrario
=0
y
E 2  Ex2  E y2
tan 
E0 y
E0 x
Figura Nº 1.- (a) Onda electromagnética linealmente polarizada en dirección vertical. (b) La
onda polarizada linealmente puede estar orientada en cualquier dirección, formando un
ángulo 
Polarización lineal de la luz -
2
Usualmente sin embargo, la luz emitida de las fuentes más comunes es no
polarizada. En este caso, la radiación de los átomos de la fuente emite trenes de onda en los
cuales los campos vectoriales eléctricos individuales son orientados en el espacio
azarosamente aunque, por supuesto, ellos se mantienen perpendiculares a la dirección de
propagación — ver figura Nº 2 —
E0x = E0y
 = azarosa
Figura Nº 2.- Onda electromagnética no polarizada. La luz no polarizada es aquella
que no tiene preferencia por algún modo de vibración particular, sino que es una
mezcla azarosa de múltiples formas de polarización, que van cambiando en cada
instante. La representación es aproximada pues la fuente emite en todas direcciones,
incluyendo hacia fuera y adentro del papel.
Cualquier estado de polarización de la onda luminosa puede ser representada por la
superposición de un par independiente de ondas “componentes” del campo eléctrico,
linealmente polarizadas y mutuamente ortogonales. Por ejemplo, las ondas cuyas
componentes de campo eléctrico están orientados a lo largo de los ejes x y y
respectivamente, se pueden escribir:
Ex  E0 x cos kz  ωt 
E y  E0 y cos kz  ωt  ε
[1]
donde  es la diferencia de fase entre las dos componentes. Mediante una cuidadosa
selección de las amplitudes E0x, E0y y de , se pueden generar cualquier estado de
polarización, incluyendo formas de polarización no lineales, tales como la polarización
circular y la elíptica.
Las principales formas mediante las cuales se puede crear la luz polarizada son
aquellas que involucran los fenómenos del dicroísmo, reflexión, birrefringencia y
esparcimiento. Los experimentos que se plantean tienen relación con los tres primeros, por
lo cual no se discutirá lo relacionado con el esparcimiento o dispersión, que es un fenómeno
asociado a la interacción de la luz con cuerpos de tamaño muy pequeño como, por ejemplo,
las moléculas de aire y que es responsable, entre otras cosas, del color azul del cielo
despejado.
Polarización lineal de la luz -
3
(i) Dicroísmo: se refiere a la propiedad de un material para absorber selectivamente uno de
las dos componentes ortogonales linealmente polarizadas de un rayo incidente no
polarizado. Tal artefacto es conocido como un polarizador y estructuralmente es
físicamente anisotrópico. Absorbe una de las componentes del campo mientras resulta
esencialmente transparente para el otro. La orientación del campo eléctrico transmitido
define una dirección conocida como el eje de transmisión del polarizador. Los bien
conocidos polaroides inventados por E. H. Land en 1938 son los polarizadores más
comúnmente utilizados. Consiste en una hoja fina de material polimérico en el cual las
largas cadenas de moléculas son alineadas tensándolas durante su manufactura.
Curiosamente, el eje de transmisión es perpendicular a la orientación de las moléculas. Si la
luz no polarizada incide sobre uno de tales polaroides, cerca de la mitad de la intensidad es
transmitida, estando linealmente polarizada en dirección paralela al eje,
independientemente de la orientación de dicho eje. Esto es consecuencia de la completa
simetría de la luz no polarizada. Suponga que ahora se introduce un segundo polaroide
idéntico, llamado analizador, cuyo eje forma un ángulo  con el primero, como se muestra
en la figura Nº 5.
Figura Nº 5. Ley de Malus. Si un haz de luz natural incide sobre un polarizador lineal
ideal, únicamente será transmitida la luz cuyo plano de vibración sea paralelo a una
dirección particular :
EL EJE DE TRASMISION
y
E cos 
z
x
E cos 
Luz
natural

E
Polarizador
Analizador
Detector
Sólo la componente E cos será transmitida a través del analizador, por tanto, si
Imax es la intensidad entre los polaroides, entonces la intensidad transmitida a través del
analizador está dada por:
I  I maxcos2θ
(LEY DE MALUS)
[2]
Por supuesto que Imax es aproximadamente I0/2 donde I0 es intensidad original
incidente. El significado del término “analizador” se hace ahora evidente — un analizador
es útil tanto para determinar si la luz está polarizada linealmente como para encontrar el
plano de polarización aplicando la Ley de Malus—
Polarización lineal de la luz -
4
(ii) Reflexión: cuando la luz es reflejada desde una interfase entre dos medios, puede estar
parcial o totalmente polarizada linealmente. Esto fue descubierto por primera vez por Sir
David Brewster. El grado de polarización depende del ángulo de incidencia y también de
los índices de refracción de los dos medios. Cuando el ángulo de incidencia es tal que los
rayos reflejado y refractado forman 90º, entonces el rayo reflejado estará completamente
polarizado. Esta situación se ilustra en la figura Nº 6 donde B, conocido como ángulo de
Brewster, es ese particular ángulo de incidencia.
Rayo incidente
(no polarizado)

56.3º

Ei

56.3º
Rayo reflejado
(polarizado)
Er
AIRE
(n1  1)
90.0º
VIDRIO
t
(n2 = 1,50)
Er
Ei
PLANO DE
INCIDENCIA
Rayo refractado
(parcialmente polarizado)
Et
56.3º
56.3º
90.0
º
(n =
1,50)
VIDRI
O
Et
Figura Nº 6. Reflexión oblicua de un haz polarizado paralelo al plano
de incidencia, bajo el ángulo de Brewster B  56,3º, para la interfase
aire-vidrio. Si el rayo incidente está polarizado en dirección paralela al
plano de incidencia no habrá ningún haz reflejado.
A partir de la geometría de la figura, θ t  90º θ B , entonces utilizando la ley de
Snell se puede escribir:
n1 sen θ B  n 2 sen θ t  n 2 sen 90º θ B   n 2 cosθ t
tan θ B 
n2
n1
(LEY DE BREWSTER)
[3]
[4]
Para el caso ilustrado se obtiene que B  56.3º. Nótese que el vector eléctrico de la
luz reflejada es perpendicular al plano de la figura, de modo que una hoja de polaroide con
su eje colocado verticalmente (lentes de sol) debería bloquear toda la luz (resplandor)
reflejada bajo el ángulo de Brewster en una superficie horizontal.
Polarización lineal de la luz -
5
(ii) Birrefringencia: Una de las características más relevantes del estado cristalino, desde
el punto de vista óptico, es la relacionada con la anisotropía de la mayoría de los cristales.
Una consecuencia de ello es que la velocidad de la luz en dichos cristales depende tanto de
la dirección de propagación como del estado de polarización de la luz. En los casos más
simples de los cristales uniaxiales tales como el cuarzo, hielo, turmalina y calcita, para
nombrar sólo algunos, se encuentra que la luz natural incidente se separa en dos rayos que
viajan con diferentes velocidades y están polarizados en direcciones mutuamente
perpendiculares. Tales cristales tienen doble refracción y se denominan birrefringentes.
Uno de los rayos invariablemente obedece la Ley de Snell y viaja con la misma velocidad
en todas las direcciones tal como ocurre con un rayo simple, con un índice de refracción
isotrópico no asociado y sus frentes de onda de Huygens son esféricos.
Por razones obvias este rayo es conocido como el rayo ordinario (rayo o). El otro
llamado rayo extraordinario (rayo e) el cual no obedece generalmente la ley de Snell ni su
velocidad es la misma en todas las direcciones. El índice de refracción para el rayo e se
encuentra entonces que varía con la dirección desde no hasta, para la calcita, un valor más
pequeño ne. El frente de onda de Huygens es ahora un elipsoide de revolución, siendo el eje
de revolución una dirección única característica del cristal conocida como eje óptico.
Los dos rayos tienen la misma velocidad ( el mismo índice no) cuando se propagan a
lo largo del eje óptico y donde sus frentes de onda son tangentes. Para la dirección
perpendicular, la diferencia de velocidad es máxima —el índice es no para el rayo o y ne
para el rayo e, tal que en la calcita, donde no < ne, el rayo e viaja más rápido—. Los estados
de polarización mutuamente ortogonales de los dos rayos pueden ser fácilmente
encontrados en todos los casos a partir de las siguientes reglas:
rayo o: la polarización es perpendicular al plano definido por el rayo o y el eje óptico y
es también tangente al frente esférico de la onda o.
rayo e: la polarización es perpendicular al plano definido por el rayo o y el eje óptico y es
también tangente al frente esférico de la onda o.
Estas consideraciones son ilustradas en la figura Nº 7 los casos más simples con el
eje óptico siendo o paralelo o perpendicular del plano de incidencia. (para una orientación
más general del eje óptico la situación es mucho más compleja).

Para la teoría electromagnética aplicada a medios materiales, el vector eléctrico fundamental es el
desplazamiento eléctrico  antes que el campo eléctrico E. La polarización de una onda luminosa es
entonces más apropiadamente descrita por la dirección de y ésta es la que se muestra en la figura Nº 7. para
el rayo o  y E son colineales. Para el rayo e,  es tangente al frente de onda en concordancia con la regla,
pero E es perpendicular al rayo tal que  y E, ambos coplanares con el eje óptico, no son colineales (excepto
para la dirección a lo largo o normal al eje óptico).
Polarización lineal de la luz -
(a) Eje óptico paralelo a la
frontera y paralelo al plano
de incidencia.
(b) Eje óptico perpendicular a
la frontera y paralelo al plano
de incidencia.
e
(c) Eje óptico paralelo a la
frontera y perpendicular al
plano de incidencia.
e
o
o
eje óptico
o
eje óptico
El rayo e no obedece la ley de
Snell, excepto en la incidencia
normal para la cual no hay
doble refracción pero la
velocidad es diferente.
El rayo e no obedece la ley de
Snell, excepto en la incidencia
normal para la cual no hay
doble refracción y la velocidad
no es diferente.
e
eje óptico
El rayo e no obedece la ley de
Snell.
Para la incidencia
normal
no hay doble
refracción y la velocidad es
diferente.
d) Eje óptico formando un ángulo con la frontera, paralelo al plano de incidente
eje óptico
eje óptico
o
e
e
o
El rayo e no obedece la ley de Snell, excepto en la incidencia normal para la cual
hay doble refracción y la velocidad es diferente.
Figura Nº 7. Comportamiento óptico de un cristal uniaxial negativo (ne < no ),
por ejemplo, la calcita (espato de Islandia)
6
Polarización lineal de la luz -
7
EXPERIMENTOS: siguiendo los procedimientos indicados realice las experiencias que a
continuación se plantean.
1. Para determinar el eje de transmisión de un polarizador: Seleccionar uno de los dos
polaroides, colocarlo en un soporte como el de la figura Nº 9 y mantenerlo en posición
vertical, con cualquiera de sus manos por el
tronco del soporte o preferiblemente en una
base del banco óptico. Mirar a través del
polaroide a alguna luz reflejada en una
superficie horizontal y rotar el polaroide en
su marco hasta que la intensidad sea
mínima. Cuidadosamente registrar la
polaroide
orientación angular porque este polaroide,
con esta orientación, será usada como un
Soporte con marco
polarizador en todos los experimentos
rotatorio graduado
siguientes. Considerando el descubrimiento
de Brewster se debería poder decidir sobre
la dirección del eje de transmisión y por lo Figura Nº 9. Soporte y cristal polaroide
tanto la polarización de la luz emergente.
2. Para observar los rayos o y e directamente y verificar si sus polarizaciones son
ciertamente mutuamente ortogonales: Tomar
el cristal de calcita y colocarlo sobre una
pequeña marca negra en un pedazo de papel.
Notar que se aprecian dos imágenes — tal
como indicaría el diagrama de la figura Nº
7(d) y como se ilustra en la figura Nº 10 —
Tomar el otro polaroide en las manos y
utilizarlo como un analizador para examinar el
estado de polarización de cada una de las
imágenes.
¿Están
las
observaciones
experimentales de acuerdo con lo esperado? A
continuación, rotar el cristal en el plano Figura Nº 10. Cristal de calcita.
horizontal y describir las observaciones.
Formación de doble imagen
3. Para verificar la Ley de Malus: — 1er Procedimiento— Montar la fotorresistencia (la
conductancia eléctrica de este dispositivo depende linealmente de la intensidad
luminosa que cae sobre ella), el polarizador y la lámpara en el banco óptico cada uno a
30 cms. del otro y ajustar su altura hasta que la fotorresistencia está centrada en el haz
de luz que pasa a través del polarizador. Conectar la fotorresistencia en el circuito
mostrado en la figura Nº 11. El voltímetro usado es un voltímetro Weston de baja
resistencia el cual en este dispositivo actúa como un amperímetro de gran resistencia,
160 . Las lecturas del voltímetro son medidas de la intensidad luminosa cayendo
sobre la fotorresistencia. El voltímetro debería estar conectado para una escala de 1.6
voltios y la fuente de corriente continua se ajusta para brindar una deflexión de fondo
escala cuando la lámpara está encendida.
Polarización lineal de la luz -
8
Colocar el analizador en el banco óptico tapando la fotorresistencia y registrar la
lectura del voltímetro para
Fuente de
0
24
varias orientaciones angulares
poder C.C.
del analizador. Se sugiere que
- +
C.C.
se tomen lecturas cada 10º (5º
acercan picos y depresiones)
hasta completar 360º rotando
Voltímetro de
el analizador. Grafique sus
+
Weston
datos tal y como los obtuvo.
¿Están los resultados gráficos
Fotorresistencia
cualitativamente de acuerdo
Figura Nº 11. Esquema del circuito
con la ley de Malus expresada
para medir indirectamente la intensidad
por la ecuación [2]?
luminosa.
4. Para verificar la Ley de Malus: — 1er Procedimiento— Montar el fotómetro como
muestra la figura Nº 12…