Version Word - econometria i :::: uns
Anuncio

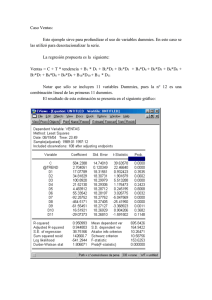
UNIVERSIDAD NACIONAL DEL SUR DEPARTAMENTO DE ECONOMÍA Econometría 2005 TRABAJO PRACTICO 3 1. Establezca si las siguientes afirmaciones son verdaderas o falsas. Justifique. a) El intervalo de confianza para una predicción media es más grande que el intervalo de confianza para una predicción individual. b) Se realizó una regresión del consumo individual con una muestra de individuos que poseían un ingreso entre $200 y $1000. Posteriormente se predice en base a la misma, por un lado, el consumo de un conjunto de individuos con un ingreso promedio de $500, y por el otro, el consumo de un conjunto de individuos con un ingreso promedio de $2000. La predicción realizada sobre el primer conjunto de individuos (ingreso prom. $500) es más exacta que la realizada sobre el segundo conjunto de individuos (ingreso prom. $2000). c) Una variable dicotómica es una variable que toma valores en el intervalo (0,1). d) Siempre que se omite una variable relevante del modelo la estimación de los parámetros del mismo es sesgada. 2. En base a una muestra de 500 familias con ingresos que variaban entre 450 y 3000 pesos, se estimó una función consumo con los siguientes resultados: Cˆ i 34,5 0,879 Yi t - stat 7.5 R 2 0.86 Y/ n = 1600 y2 = 120000 u2 = 8200 En base a ello, obtener: a) El intervalo de confianza para el consumo del conjunto de familias cuyos ingresos promedio son $2100. b) el intervalo de confianza para el consumo de una familia cuyo ingreso promedio es $2100. 3. Una compañía de seguros desea estimar la probabilidad de que una persona asegurada tenga un accidente de automóvil, en función de distintas características de la misma. Para ello utiliza el siguiente modelo: pi 0,0015 0,04 Ei 0,008 Ai 0,00028 0,011 0,002 i 1, ...,60 donde los errores estándar aparecen entre paréntesis debajo de los coeficientes estimados y donde: UNIVERSIDAD NACIONAL DEL SUR DEPARTAMENTO DE ECONOMÍA Econometría 2005 pi es la probabilidad de accidente del asegurado (en tanto por uno), Ei es una variable binaria que tomará valor 1 si el asegurado es menor a 30 años y 0 en caso contrario Ai es la antiguedad del automóvil a) Escribir el valor numérico de la variable dicotómica suponiendo que la muestra ha sido ordenada de manera que las personas con menos de 30 años (que constituyen el 25% de la muestra) son las primeras observaciones. b) Contrastar la significatividad de la variable dicotómica interpretando su resultado 4. En la web de la cátedra la base de datos ephgbamay03.xls contiene datos de la EPH (Encuesta Permanente de Hogares) correspondiente a la onda de Mayo del 2003 para el aglomerado Gran Buenos Aires (Capital Federal y Gran Buenos Aires). La misma contiene 1839 observaciones, dado que se han eliminado observaciones que correspondian a individuos que se encontraban en una situación laboral distinta a la de ocupados, que tenian un ingreso horario igual a cero y/o poseian un nivel educativo inferior al primario incompleto. Las variables contenida en la misma son: inghora: ingreso horario edupi: igual a 1 si el individuo posee educación primaria incompleta edup: igual a 1 si el individuo posee educación primaria completa edusi: igual a 1 si el individuo posee educación secundaria incompleta edus: igual a 1 si el individuo posee educación secundaria completa eduui: igual a 1 si el individuo posee educación universitaria incompleta eduu: igual a 1 si el individuo posee educación universitaria completa edad: edad del individuo edadsq: edad del individuo al cuadrado sexo: igual a 1 si el individuo es masculino a) Realice una regresión de Mincer de los salarios horarios en función de dummies educativas, del sexo, edad y edad al cuadrado. - Realice dicha regresion por MCO incluyendo el termino constante y dejando afuera la variable edupi y realice una regresion adicional considerando dicha variable pero sin considerar el termino constante. Compare ambas regresiones. - Se puede realizar dicha regresión considerando todas las variables dummies y el término constante. Justifique. b) Realice un análisis de los retornos a la educación considerando, por un lado, un individuo de 40 años de sexo masculino, y por el otro, un individuo de 40 años de sexo femenino (preferentemente con un gráfico). 5. Considere la regresión realizada en el ejercicio 4 y responda: Sobre que supuestos se basa una regresión que en lugar de utilizar las variables dummies educacionales utilizara una variable denominada educ que representa los años de educación que posee el individuo. UNIVERSIDAD NACIONAL DEL SUR DEPARTAMENTO DE ECONOMÍA Econometría 2005 6. A partir de una serie de datos acerca de n familias de una determinada ciudad se desea estimar una función de ahorro. Se considera que además del ingreso de cada familia, deben tenerse en cuenta otras variables relacionadas con el jefe de familia: el grupo etareo al que pertenece ( menor de 25 años, entre 25 y 55 años o mayor de 55 años), el nivel educativo (primario , secundario completo, terciario completo), su categoría ocupacional ( ejecutivo, obrero o empleado, cuentapropista, patrón o empleador), el sector de la actividad en que se desempeña ( agricultura, industria, comercio, servicios, construcción). También se considera que la propiedad de la vivienda podría ser una variable relevante. a) Plantee el modelo definiendo claramente cada una de las variables. b) ¿Cuál sería la función de regresión para una familia, propietaria de la casa que habita y cuyo jefe pertenece al segundo grupo etáreo, tiene estudios secundarios completos y se desempeña como empleado en el sector servicios? c) Describa paso a paso como testearía las siguientes hipótesis: c1) el comportamiento con respecto al ahorro de un cuentapropista es el mismo que el de un obrero o empleado c2) el sector de actividad no tiene incidencia sobre el comportamiento con respecto al ahorro. Explique en cada caso las regresiones que correría, los estadísticos que utilizaría para testear las hipótesis, sus distribuciones, los criterios de rechazo, etc. 7. El gasto en indumentaria de una familia depende del ingreso de la misma (Y) así como del número de integrantes (N). Se encuestaron familias de áreas rurales y urbanas y se formularon los siguientes modelos: Gri = a + b Yri + c Nri + ui ( i= 1,2,........m) Guj = d + e Yuj + f Nuj + uj ( j= 1,2,........n) a) ¿Cuál es la interpretación económica de la hipótesis a = d? ¿Cómo la testearía? b) ¿Cuál es la interpretación económica de la hipótesis b = e? ¿Cómo la testearía? c) ¿Cuál es la interpretación económica de la hipótesis c= f? ¿Cómo la testearía? a) ¿Cómo testearía la hipótesis de que la función es totalmente distinta en ambas áreas? 8. Un modelo que explica el precio de un bien en términos de sus características se denomina modelo de precio hedónico. La ecuación siguiente es un modelo de este tipo para el precio de la las viviendas (PREC) (variable endógena, medida en miles de pesos). Las variables explicativas son superficie (SUP) en m2, número de habitaciones (HAB), y número de baños (BAN). Utilizando 19 observaciones sobre casas que se vendieron en una ciudad de EEUU en 1990 se estimó la siguiente ecuación: PREC = 7.46 + 0.634 SUP – 0.066 HAB + 0.158 BAN (1.15) (0.184) (0.059) (0.035) R2= 0.816 R2= 0.803 UNIVERSIDAD NACIONAL DEL SUR DEPARTAMENTO DE ECONOMÍA Econometría 2005 En base a esos resultados determine si las siguientes afirmaciones son verdaderas o falsas y corrija donde corresponda: a) La elasticidad precio respecto a la superficie es 0,634, lo que implica que si se mantienen fijos el número de habitaciones y de baños, un aumento del 1% en la superficie aumenta el precio de la vivienda en 0.634% b) Ceteris Paribus, un baño más en la vivienda aumentaría su precio en 158 pesos, pero la variables resulta estadísticamente no significativa c) Con un 95% de confianza podemos decir que el intervalo 0.2418 1.026 contiene al valor poblacional del coeficiente que acompaña a la variable SUP, lo que permite confirmar la no significatividad de la misma. d) El resultado obtenido muestra que la variable HAB no es significativa, lo que evita realizar consideraciones relativas a que su signo es contrario al esperado e) Aunque el 80% de la variabilidad del precio de las viviendas parece explicado por las variables incorporadas al modelo el investigador desconfía de los resultados por entender que sus estimaciones son sesgadas, ya que reconoce que ha omitido incluir una variable muy importante como es la localización de la vivienda (medida en términos de la distancia al centro comercial de la ciudad) f) Realizó la reformulación del modelo para incorporar ese aspecto utilizando una variable dummy (D) a la que dio valor 1 cuando la vivienda estaba localizada a menos de diez cuadras del centro comercial y 0 en caso contrario, con lo que obtuvo los siguientes resultados: PREC = 7.54 + 0.686 SUP– 0.052 HAB + 0.218 BAN + 0.123 D (1.05) (0.188) (0.039) (0.035) (0.081) R2= 0.856 R2= 0.783 En base a los mismos concluyó que la variable localización era realmente relevante, aunque no encontró forma de plantear un modelo que mostrara que la incidencia de la superficie sobre el precio es distinta según la localización de las viviendas.