El problema del vendedor de diarios: en este ejemplo hay un único
Anuncio
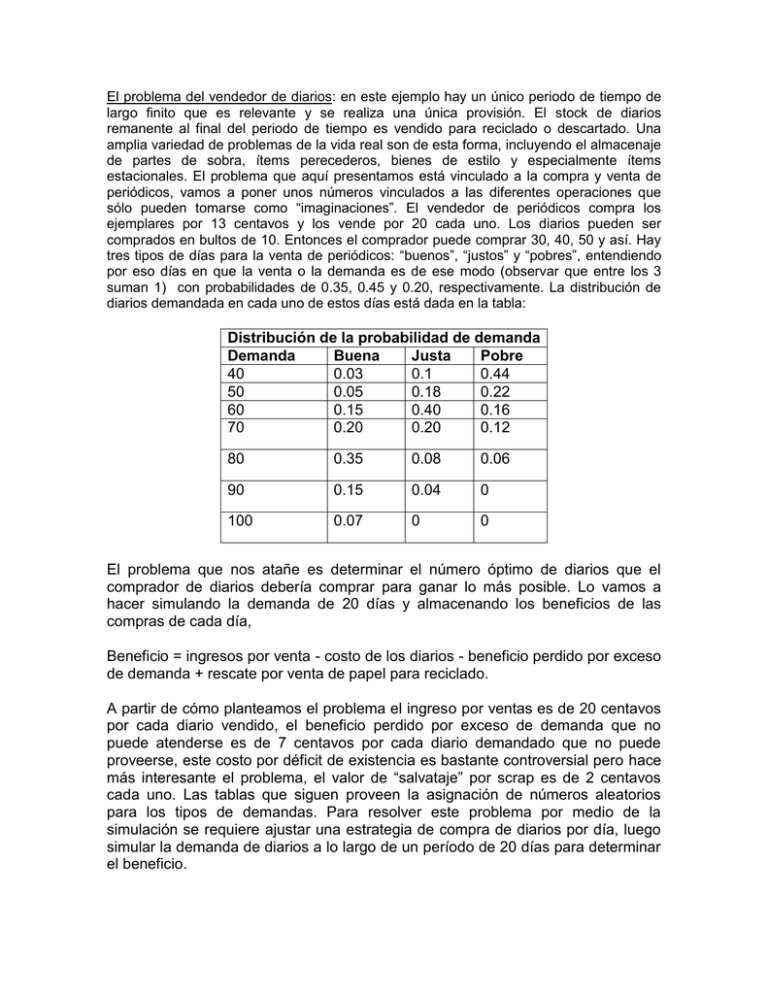
El problema del vendedor de diarios: en este ejemplo hay un único periodo de tiempo de largo finito que es relevante y se realiza una única provisión. El stock de diarios remanente al final del periodo de tiempo es vendido para reciclado o descartado. Una amplia variedad de problemas de la vida real son de esta forma, incluyendo el almacenaje de partes de sobra, ítems perecederos, bienes de estilo y especialmente ítems estacionales. El problema que aquí presentamos está vinculado a la compra y venta de periódicos, vamos a poner unos números vinculados a las diferentes operaciones que sólo pueden tomarse como “imaginaciones”. El vendedor de periódicos compra los ejemplares por 13 centavos y los vende por 20 cada uno. Los diarios pueden ser comprados en bultos de 10. Entonces el comprador puede comprar 30, 40, 50 y así. Hay tres tipos de días para la venta de periódicos: “buenos”, “justos” y “pobres”, entendiendo por eso días en que la venta o la demanda es de ese modo (observar que entre los 3 suman 1) con probabilidades de 0.35, 0.45 y 0.20, respectivamente. La distribución de diarios demandada en cada uno de estos días está dada en la tabla: Distribución de la probabilidad de demanda Demanda Buena Justa Pobre 40 0.03 0.1 0.44 50 0.05 0.18 0.22 60 0.15 0.40 0.16 70 0.20 0.20 0.12 80 0.35 0.08 0.06 90 0.15 0.04 0 100 0.07 0 0 El problema que nos atañe es determinar el número óptimo de diarios que el comprador de diarios debería comprar para ganar lo más posible. Lo vamos a hacer simulando la demanda de 20 días y almacenando los beneficios de las compras de cada día, Beneficio = ingresos por venta - costo de los diarios - beneficio perdido por exceso de demanda + rescate por venta de papel para reciclado. A partir de cómo planteamos el problema el ingreso por ventas es de 20 centavos por cada diario vendido, el beneficio perdido por exceso de demanda que no puede atenderse es de 7 centavos por cada diario demandado que no puede proveerse, este costo por déficit de existencia es bastante controversial pero hace más interesante el problema, el valor de “salvataje” por scrap es de 2 centavos cada uno. Las tablas que siguen proveen la asignación de números aleatorios para los tipos de demandas. Para resolver este problema por medio de la simulación se requiere ajustar una estrategia de compra de diarios por día, luego simular la demanda de diarios a lo largo de un período de 20 días para determinar el beneficio. Tipo de demanda Buena Justa Pobre Probabilidad 0.35 0.45 0.2 Acumulada 0.35 0.80 1 Distribución acumulada Demanda Buena justa Pobre 40 0.03 0.1 0.44 50 0.08 0.28 0.66 60 0.23 0.68 0.82 70 0.43 0.88 0.94 80 0.78 0.96 1 90 0.93 1 1 100 1 1 1 Random Lumber asignado 01-35 36-50 81-00 Asignación de random number buena Justa Pobre 01-03 01-10 01-44 04-08 11-28 45-66 09-23 29-68 67-82 24-43 69-88 83-94 44-78 89-96 95-00 79-93 97-00 94-00




