Circuitos_de_Corriente_Continua

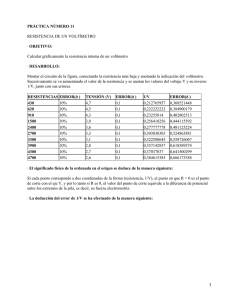
Índice
Resumen ________________________________________________________________ 2
Introducción _____________________________________________________________ 2
Método experimental ______________________________________________________ 5
Parte A: Instrumentos de medición ___________________________________________ 5
Parte B: Determinación de la relación funcional entre ΔV e I ______________________ 5
Parte C: Construcción de un divisor de tensión _________________________________ 6
Parte D: Métodos para determinar el valor de una resistencia _____________________ 6
Propagación de errores _____________________________________________________ 7
Resultados _______________________________________________________________ 7
Parte A: Instrumentos de medición ___________________________________________ 7
Parte B: Determinación de la relación funcional entre ΔV e I ______________________ 8
Parte C: Construcción de un divisor de tensión _________________________________ 9
Parte D: Métodos para determinar el valor de una resistencia ____________________ 11
Conclusión _____________________________________________________________ 12
Referencias _____________________________________________________________ 13
-1-
Resumen
Los objetivos de esta práctica de laboratorio son: familiarizarse con la utilización de
instrumentos para mediciones eléctricas; encontrar una relación funcional entre la corriente y la
diferencia de potencial en conductores; construir un divisor de tensión a partir de una fuente de
tensión fija; y determinar el valor de una resistencia incógnita.
Introducción
Para la medición de variables eléctricas, se utilizan generalmente dos tipos de
instrumentos:
 Voltímetro: se utiliza para medir la diferencia de potencial entre dos puntos de un
circuito eléctrico.
 Amperímetro: se utiliza para medir la intensidad de corriente que circula por un
conductor.
Si se quiere medir simultáneamente la diferencia de potencial y la intensidad de
corriente, existen dos tipos de conexiones denominadas conexión corta del voltímetro o
amperímetro afuera y conexión larga del voltímetro o amperímetro adentro (Figura 1).
Figura 1. Distintas conexiones del voltímetro y el amperímetro.
Si se utiliza la conexión corta o amperímetro afuera, la corriente que pasa por el
amperímetro es la suma de las corrientes que pasan por la resistencia y por el voltímetro
I  I R  IV . Por lo tanto, la resistencia calculada y la corriente medida no corresponden a la
resistencia R , sino a la equivalente de R y RV en paralelo:
Rcalculado 
R  RV
R  RV
-2-
(1)
Esto implica un error absoluto:
R  Rcalculado  R  
R2
R  RV
(2)
Y un error relativo igual a:
R  
R
R  RV
(3)
Se observa que el error es negativo, lo cual significa que el valor calculado siempre es
menor que el valor verdadero.
Si se quiere medir correctamente el valor de la intensidad de corriente que pasa por la
resistencia, se debe realizar la conexión larga o amperímetro adentro. En este caso, la corriente
que pasa por el amperímetro es la misma que la que pasa por la resistencia; pero la diferencia de
potencial que lee el voltímetro es la suma de la del amperímetro y de la resistencia. Por lo tanto,
la resistencia calculada en este caso, corresponde al equivalente de R y RA en serie:
Rcalculado  R  RA
(4)
R  Rcalculado  R  RA
(5)
Esto implica un error absoluto:
Y un error relativo igual a:
R 
RA
R
(6)
El error es positivo, lo que significa que el valor calculado es mayor que el verdadero.
Al comparar los errores relativos de ambas conexiones, se observa que mientras el error
de la conexión corta aumenta con la resistencia, el de la conexión larga disminuye. Por lo tanto,

hay un valor R para el cual ambas conexiones tienen el mismo error relativo. Si se desprecia
RA
frente a R resulta que:
2
R  RA  RV
-3-
(7)
De esto, se concluye que si la resistencia a determinar es mayor que R conviene utilizar
la conexión larga y, por el contrario, si es menor que R conviene utilizar la conexión corta.
Un instrumento utilizado para determinar el valor de una resistencia con una precisión
media, es el óhmetro. Su funcionamiento se detalla en la (Figura 2):
Figura 2. Funcionamiento del óhmetro.
Donde  0 es la diferencia de potencial de la fuente, RL la resistencia limitadora y R la
resistencia cuyo valor se quiere determinar.
En muchas ocasiones, es necesario alimentar elementos a diferencias de potenciales
distintas. Esto, se puede lograr mediante un dispositivo denominado divisor de tensión (Figura
3).
Figura 3. Divisor de tensión.
Donde  0 es la diferencia de potencial de la fuente, R1 Y R2 son dos tramos de
resistencias conectadas en serie por donde se produce una caída de potencial V1  R1  I en R1
Y V2  R2  I en R2.
-4-
Método experimental
Parte A: Instrumentos de medición.
En esta parte del trabajo, se analizan los instrumentos que se utilizan a lo largo de la
práctica de laboratorio. Se toma nota de su principio de funcionamiento, rangos, precisión, datos
consignados mediante símbolos y su correspondencia.
Parte B: Determinación de la relación funcional entre la diferencia de potencial y la intensidad
de corriente en conductores.
El objetivo de esta parte del trabajo es determinar una relación funcional entre  V e I .
Para establecer esta dependencia, se utilizan un voltímetro y un amperímetro en su
versión de conexión corta y se mide la intensidad de corriente que circula por el conductor
cuando se aplican diferencias de potenciales distintas sobre el mismo (Figura 4).
Figura 4. Circuito utilizado para determinar la relación entre ΔV e I.
En primer lugar, se arma el circuito como el que se muestra en la (Figura 4). Luego, se
determina el valor máximo de potencial que envía la fuente y los valores nominales de la
resistencia ( R ) . Una vez hecho esto, se varía la diferencia de potencial que envía la fuente entre
0 y el valor máximo en forma regular, de manera de obtener entre 10 y 15 valores. Luego, para
cada uno de esos valores se mide la diferencia de potencial y la intensidad de corriente que
circula. Finalmente, se confecciona un grafico con los valores obtenidos para determinar la
ecuación que relaciona a  V con I .
-5-
Parte C: Construcción de un divisor de tensión.
En esta parte se busca construir un divisor de tensión como el que se muestra en la
(Figura 3). Para ello, se conecta una fuente de tensión fija ( 0 ) a una resistencia limitadora
( RL ) , que a su vez se conecta en serie con una resistencia RR  R1  R2 . Luego se conecta al
circuito un voltímetro en paralelo, cuyos bornes se desplazan continuamente definiendo valores
para R1 y R2 .
Luego se miden las distintas tensiones que se producen al variar el punto de conexión del
voltímetro en el circuito. Finalmente, se mide V en función de R2 y se lo representa
gráficamente para, de esta manera, obtener la relación de dependencia mediante el ajuste de
cuadrados mínimos.
Parte D: Métodos para determinar el valor de una resistencia.
En primer lugar, mediante un óhmetro se miden los valores de las resistencias que se
utilizan en este trabajo.
Luego, se comparan estos valores con los valores nominales para determinar la validez
del trabajo.
En segundo lugar, se quiere determinar el error para distintas resistencias ( R ) en los
casos que se utiliza:

El método de voltímetro-amperímetro en su versión corta (amperímetro afuera).

El método de voltímetro-amperímetro en su versión larga (amperímetro adentro).
Primero, se determinan las resistencias internas del amperímetro y del voltímetro.
En el método del amperímetro afuera, se utiliza un circuito como el que se muestra en la
(Figura 4). Luego, se calculan el Rcalculado , su error absoluto y su error relativo a través de las
ecuaciones (1), (2) y (3) respectivamente.
En el método del amperímetro adentro, se utiliza un circuito como el que se observa en la
(Figura 5). Luego, al igual que en el caso anterior, se calculan el Rcalculado , su error absoluto y su
error relativo a través de las ecuaciones (4), (5) y (6) respectivamente.
-6-
Figura 5. Método de voltímetro-amperímetro en su conexión larga del voltímetro.
Propagación de errores:
Los errores que se cometen a lo largo de la experiencia son debidos a los instrumentos
utilizados.
Error del voltímetro:
Vmed 
nº .de.clase
 ( Alcance.en.unidades )
100
 alcance.en.unidades 
Vap  0,5  

 alcance.en.divisiones 
V  (Vmed  Vap )
Resultados
Parte A: Instrumentos de medición.

Voltímetro: Posee una escala en rojo para medir la diferencia de potencial en
corriente alterna y otra escala en color negro para medir la diferencia de potencial en
corriente continua. También tiene un espejo que sirve para evitar el error que produce
el observador. Tiene 150 divisiones.

Amperímetro: Es similar al voltímetro; pero posee 100 divisiones en lugar de las 150
del voltímetro.

Multímetro: Es de tipo digital y se lo utiliza como un óhmetro.
-7-
Parte B: Determinación de la relación funcional entre la diferencia de potencial y la intensidad
de corriente en conductores.
La (Tabla 1) muestra la diferencia de potencial y la intensidad de corriente medida para
las distintas diferencias de potenciales que eroga la fuente:
0
V
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
ΔV
V
0,8
1,8
2,8
3,6
4,6
5,6
6,4
7,4
8,4
9,4
I
mA
10,0
20,0
27,5
37,5
45,0
55,0
65,0
75,0
85,0
95,0
Tabla 1. Medición de ΔV e I para las distintas diferencias de potenciales que envía la fuente.
En el (Gráfico 1) se presenta como varía la diferencia de potencial a medida que aumenta
la intensidad de corriente:
10,0
9,0
y = 0,1005x - 0,0968
8,0
R2 = 0,9985
ΔV (V)
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
0,0
20,0
40,0
60,0
80,0
100,0
I (mA)
Gráfico 1. Relación entre ΔV e I para las distintas diferencias de potenciales que envía la fuente.
-8-
En el (Gráfico 1) se puede observar a través del método de cuadrados mínimos que  V e
I poseen una relación del tipo lineal.
Los errores que se cometen al medir la diferencia de potencial y la intensidad de
corriente son propios de los instrumentos utilizados.
Los errores de medición del voltímetro y del amperímetro son:
Vmed  0,8.V y Amed  0,01.A
Los errores de apreciación del voltímetro y del amperímetro son:
Vap  0,1.V y Aap  0,003.A
Luego los errores totales del voltímetro y del amperímetro son:
V  0, 9.V y A  0, 02. A
Parte C: Construcción de un divisor de tensión.
La (Tabla 2) muestra como varía la diferencia de potencial en función del largo de la
resistencia:
Largo de R
cm
33,0
30,0
27,0
24,0
21,0
18,0
15,0
12,0
9,0
6,0
3,0
0,0
ΔV
V
15,8
14,6
13,2
11,6
10,2
8,8
7,2
5,8
4,2
3,0
1,2
0,0
R
Ω
790,0
730,0
660,0
580,0
510,0
440,0
360,0
290,0
210,0
150,0
60,0
0,0
Tabla 2. Muestra como varía ΔV en función del largo de R.
-9-
El (Gráfico 2) muestra la relación que existe entre la diferencia de potencial ( V ) y el
tramo de resistencia ( R2 ) :
18,0
16,0
y = 0,0198x + 0,0738
14,0
2
R = 0,9995
ΔV (V)
12,0
10,0
8,0
6,0
4,0
2,0
0,0
0,0
200,0
400,0
600,0
800,0
1000,0
R (Ω)
Gráfico 2. Muestra la relación entre ΔV y R.
Los errores que se cometen al medir la diferencia de potencial, al igual que en la parte B,
son propios del instrumento.
El error de medición del voltímetro es:
Vmed  0, 8.V
El error de apreciación del voltímetro es:
Vap  0,1.V
El error total del voltímetro es:
V  0, 9.V
- 10 -
Parte D: Métodos para determinar el valor de una resistencia.

Óhmetro:
La (Tabla 3) muestra los valores nominales de tres resistencias comparadas con los
valores medidos con un óhmetro:
Resistencia
R1
R2
Valor nominal Valor medido
Ω
Ω
10,0
10,0
100,0
100,1
R3
1000,0
1011,0
Tabla 3. Muestra la relación entre los valores nominales y medidos de R.

Voltímetro-Amperímetro:
En la (Tabla 4) se presentan las resistencias internas del amperímetro y del voltímetro
utilizados:
RA
Ω
1,110426
RV
Ω
16240000
Tabla 4. Resistencias internas del amperímetro y del voltímetro.
Luego, a partir de la ecuación (7) se obtiene R * :
R*  4246,5655
La (Tabla 5) muestra los valores de Rcalculado comparados con los valores nominales de R
para la conexión corta o amperímetro afuera:
Rnominal
Ω
10
100
1000
Rcalculado
Ω
10,00
99,99
999,94
ΔR
εR
Ω
-0,000006
-0,0006
-0,06
-0,0000006
-0,000006
-0,00006
Tabla 5. Muestra la comparación entre Rcalculado y Rnominal en la conexión corta del voltímetro.
Se observa que en todos los casos el valor calculado de R es menor que el nominal,
como era de esperarse por lo que predicen las ecuaciones (1), (2) y (3).
- 11 -
La (Tabla 6) muestra los valores de Rcalculado comparados con los valores nominales de R
para la conexión larga o amperímetro adentro:
Rnominal
Ω
10
100
1000
Rcalculado
Ω
11,11
101,11
1001,11
ΔR
εR
Ω
1,1
1,1
1,1
0,1
0,01
0,001
Tabla 6. Muestra la comparación entre Rcalculado y Rnominal en la conexión larga del voltímetro.
A diferencia del caso anterior, se observa que los valores de Rcalculado son en todos los
casos mayores que el nominal, como se esperaba por lo que predicen las ecuaciones (4), (5) y
(6).
Conclusión
En la parte B, se verifica que la diferencia de potencial ( V ) posee una relación de
dependencia lineal con la intensidad de corriente ( I ) .
En la parte C, se verifica que al variar el largo de la resistencia, la diferencia de potencial
que mide el voltímetro varía entre 0 y un valor máximo. También se observa que al graficar  V
en función de R2 se obtiene una relación lineal entre las variables.
En la parte D, se observa que los valores de las resistencias incógnitas medidas con un
óhmetro se aproximan bastante bien a los valores nominales de las mismas.
Al utilizar el método del voltímetro amperímetro, se puede observar que si se utiliza le
versión corta, el valor de R calculado es siempre menor que el valor nominal; esto se debe a que
 R y  R siempre son negativos como se observa en las ecuaciones (2) y (3). En cambio, al
utilizar la versión larga, el valor de R calculado es siempre mayor que el valor nominal; esto se
debe a que, en este caso,  R y  R siempre son positivos.
Por último, se puede observar que a medida que la resistencia incógnita es más grande, el
R calculado con la versión larga del voltímetro es más preciso que la versión corta y viceversa.
Se puede notar que el valor en el que ambas conexiones coinciden es R*  4246,5655 como
predice la ecuación (7).
- 12 -
Referencias
 www.lirweb.com.ar
 Apuntes de clase.
 “Física Universitaria” Volumen 2, Sears, Zemansky, Young, Freedman.
Correos electrónicos:
(a) mache_memmolo@hotmail.com
(b) fmoirano@msn.com
(c) aguspuentes@gmail.com
- 13 -