Documento 30186

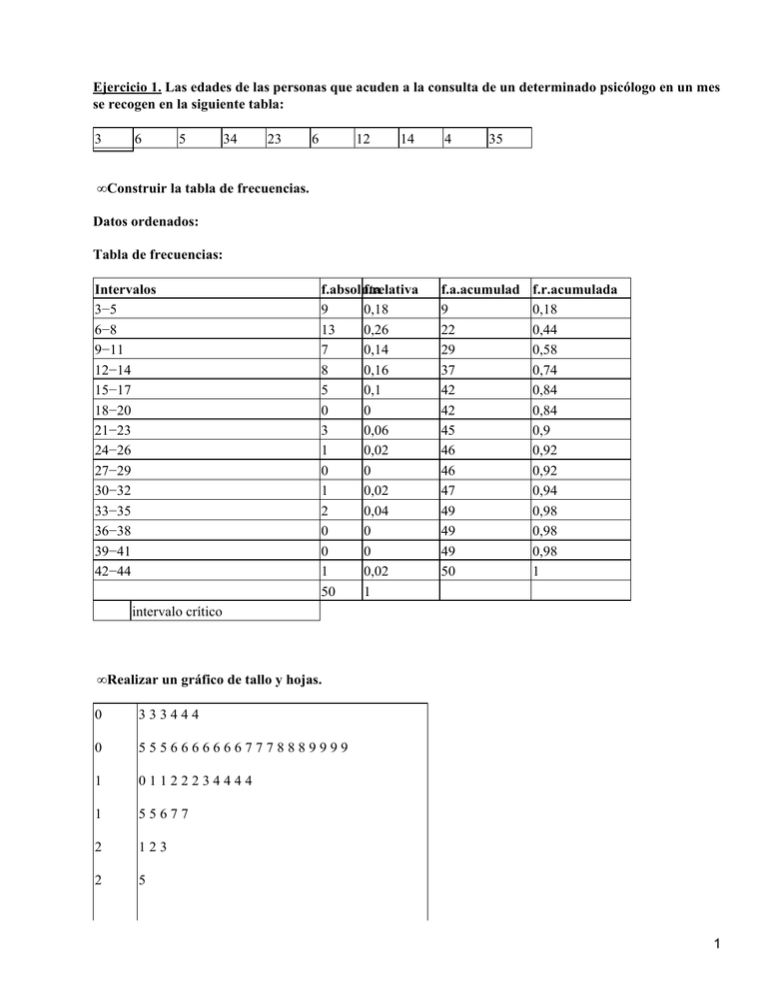
Ejercicio 1. Las edades de las personas que acuden a la consulta de un determinado psicólogo en un mes
se recogen en la siguiente tabla:
3
6
5
34
23
6
12
14
4
35
• Construir la tabla de frecuencias.
Datos ordenados:
Tabla de frecuencias:
Intervalos
3−5
6−8
9−11
12−14
15−17
18−20
21−23
24−26
27−29
30−32
33−35
36−38
39−41
42−44
f.absoluta
f.relativa
9
0,18
13
0,26
7
0,14
8
0,16
5
0,1
0
0
3
0,06
1
0,02
0
0
1
0,02
2
0,04
0
0
0
0
1
0,02
50
1
f.a.acumulad
9
22
29
37
42
42
45
46
46
47
49
49
49
50
f.r.acumulada
0,18
0,44
0,58
0,74
0,84
0,84
0,9
0,92
0,92
0,94
0,98
0,98
0,98
1
intervalo crítico
• Realizar un gráfico de tallo y hojas.
0
333444
0
55566666667778889999
1
01122234444
1
55677
2
123
2
5
1
3
24
3
5
4
2
4
• Realizar la representación gráfica mediante histograma.
d. Hallar la mediana de la distribución.
Mdn = ( n+1 ) 2
Mdn = ( 50 + 1 ) 2
Mdn = 25,5
La mediana estaría entre el dato 25 y el dato 26, es decir, entre 9 y 9. Por lo tanto
MEDIANA = 9
Ejercicio 2. Se ha pasado un test de autoritarismo a determinado grupo. Los resultados se muestran en
la siguiente tabla de frecuencias:
Intervalos
15−19
20−24
25−29
30−34
35−39
40−44
45−49
f.absolutas
48
171
60
21
12
16
6
2
50−54
3
• Completar la tabla con la marca de clase, frecuencias absolutas acumuladas, frecuencias relativas y
frecuencias relativas acumuladas.
m.clase
17
22
27
32
37
42
47
52
Intervalos
15−19
20−24
25−29
30−34
35−39
40−44
45−49
50−54
f.absoluta
48
171
60
21
12
16
6
3
337
f.a.acumulad
48
219
279
300
312
328
334
337
f.relativa
0,142
0,507
0,178
0,062
0,036
0,047
0,018
0,01
1
f.r.acumulada
0,142
0,649
0,827
0,889
0,925
0,972
0,99
1
intervalo crítico
• Dibujar el histograma de frecuencias absolutas.
• ¿Qué podriamos decir de dicho grupo respecto del autoritarismo?
El grupo presenta una distribución asimétrica (sesgada positiva) en la que encontramos una frecuencia del
50,7% en el intervalo de edad comprendido entre 20y 24 años, mientras que la frecuencia disminuye a medida
que avanzamos por la cola de la distribución. En el último intervalo estaría la frecuencia más baja (0,1%) que
correspondería al grupo comprendido entre 50 y 54 años.
• Hallar la media, varianza y desviación típica.
Media.− øX = " (f · X) / N
X
17
22
27
32
37
42
47
52
276
f
48
171
60
21
12
16
6
3
337
f.X
816
3762
1620
672
444
672
282
156
8424
MEDIA = 24,997
Varianza.−
S2 = ( 1/ N − 1) · [ "( f · x2 ) − (" f · x ) 2 / N] N = " f
3
x
17
22
27
32
37
42
47
52
276
f
48
171
60
21
12
16
6
3
337
f.x
816
3762
1620
672
444
672
282
156
8424
x2
289
484
729
1024
1369
1764
2209
2704
f.x2
13872
82764
43740
21504
16428
28224
13254
8112
227898
S2 = 1 337−1 (227898 − 84242 337)
Varianza = 51,623
Desviación típica.−
Desviación Típica = "¯¯varianza
Desviación tip. = 7,185
Ejercicio 3. Los resultados en un test de cálculo realizado a 30 alumnos han sido los siguientes:
Puntuación
Número de alumnos
12
1
13
2
14
3
15
8
16
6
17
5
18
3
19
2
• Completar la tabla de frecuencias.
x
12
13
14
15
16
17
18
19
f.absoluta
f.a.acumulada f.relativa
1
1
0,0333
2
3
0,0667
3
6
0,1
8
14
0,2666
6
20
0,2
5
25
0,1667
3
28
0,1
2
30
0,0667
30
1
b. Hallar la media aritmética y la desviación típica.
f.r.acumulada
0,0333
0,1
0,2
0,4666
0,6666
0,8333
0,9333
1
intervalo crítico
__
Media aritmética. X
__ __
4
X = f · x n => X = 473 30
MEDIA = 15,767
Desviación típica. S
S2 = 1 N − 1 [ " f · x2 − ( " f · x )2 / N ]
S2 = 3,0124038
Desviación tipica = 1,7356
• Hallar la mediana y la moda.
Mediana.
Mdn = LIR + [( p · N ) − SFI / f ] · h
En el ejercicio los datos son:
LIR = 15,5
P = 0,5
N = 30
SFI = 14
f=6
h=1
Mediana = 15,6667
Moda. Mo. Dato x con mayor frecuencia
Moda = 15
Ejercicio 4. Responder a las siguientes cuestiones:
• Sean dos series estadísticas X e Y formadas por n números,
X = { x 1, x 2, ..., x n }
Y = { y 1 , y 2 , ..., y n}
Hallar la media aritmética de la serie:
Z = X + Y = { x 1+ y 1 , x 2 + y 2 , ..., x n + y n }
en función de las medias de X e Y.
5
__ __
X = x / n x => x = X · n x
__ __
Y = y / n y => y = Y · n y
__ __ __ __
Z = ý x + y ý / ý n x + n y ý => Z = [ ý n x · X ý + ý n y · Y ý ] / ( n x + n y )
__ __ __
Z=(nxX+nyY)/(nx+ny)
• Sea una serie estadística X formada por números, X = { x 1 , x 2 , ..., x n } .
Si cada elemento de la serie se multiplica por un mismo números k, hallar la media de la nueva serie.
X = { x 1 , x 2 ,..., x n }
Z = { k · x1 , k · x 2 , ..., k · x }
__ __
Z = ( k · x n) / n x => Z = k · " x n / n x =>
__ __
Z=k·X
• Sea una serie estadística X formada por n números, X = { x 1 , x 2 , ..., x n }.
Si a cada elemento de la serie se le multiplica por un mismo número k, hallar la
Varianza de la nueva serie. __ __
Dato: la media de la nueva serie es X k = k · X
__ __ __
Xk=Zn=k·X
X = { x 1 , x 2 , ... , x n }
Z = { k · x 1 , k · x 2 , ... , k · x n }
__ __
Zn=k·X
6
__ __
S x 2 = [ ( X − X )2 ] / ( N − 1 ) => S z 2 = [ k 2 ( X − X ) 2 ] / ( N − 1 )
__
Sz2=k2 (X−X)2/(N−1)
S z 2 = k 2 · S x2
Ejercicio 5. Se ha aplicado un test de aptitud mecánica a 90 demandantes de empleo obteniéndose el
siguiente resultado:
Intervalos
50−54
54−58
58−62
62−66
66−70
70−74
74−78
fi
7
10
16
20
18
11
8
90
• Calcular los cuartiles y el percentil 45.
52
50−54 7 7 364 2704
7