ig12: estadística de itig. prácticas de statgraphics.
Anuncio

IG12: ESTADÍSTICA DE ITIG. PRÁCTICAS DE STATGRAPHICS.
PRÁCTICA 3: DISTRIBUCIONES. TEORÍA
Nombre y Apellidos............................................................... Grupo ....
Los gráficos y las tablas de frecuencias que no caben en su apartado,
incluirlos en la parte de atrás del folio o en otro folio.
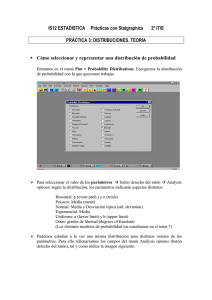
Cómo seleccionar y representar una distribución de probabilidad
Entramos en el menú Plot > Probability Distributions. Escogemos la distribución
de probabilidad con la que queremos trabajar.
Para seleccionar el valor de los parámetros botón derecho del ratón Analysis
options: según la distribución, los parámetros indicarán aspectos distintos.
Binomial: p (event prob.) y n (trials)
Poisson: Media (mean)
Normal: Media y Desviación típica (std. deviation)
Exponencial: Media
Uniforme: a (lower limit) y b (upper limit)
Otras: grados de libertad (degrees of freedom)
Podemos estudiar a la vez una misma distribución para distintos valores de los
parámetros. Para ello rellenaríamos los campos del menú Analysis options (botón
derecho del ratón), tal y como indica la imagen siguiente:
PRÁCTICAS DE STATGRAPHICS
Gráficos:
Graphical options (botón azul). De momento nos van a interesar las dos primeras :
-
Density/Mass Function: dibuja la función de densidad (caso continuo) o de
probabilidad (caso discreto): f(x) .
CDF (Cumulative density function): dibuja la función de distribución
acumulada: F(x).
Cálculo de la función de distribución (probabilidades)
Una vez seleccionada la distribución con los parámetros correctos (uno o varios,
según nos interese), podemos calcular distintas probabilidades Tabular options
(botón amarillo) Cumulative Distribution. Además con Pane Options (botón
derecho del ratón), podemos escoger los valores que interesen.
Variables discretas y continuas: lower tail area: P(X<x)
Variables discretas y continuas: upper tail area: P(X>x)
Variables discretas: probability mass: P(X=x)
Variables continuas: probability density : f(x)
PRÁCTICA 3: Distribuciones.
2
PRÁCTICAS DE STATGRAPHICS
Recuerda: F(x) = P(X x)
Cálculo de los valores críticos
En el apartado anterior hemos calculado probabilidades, pero ¿cómo calcular aquel
valor a de la variable tal que Pr X a 0.95 ? a es el 0.95-cuantil .
En la misma ventana en la que estamos trabajando hasta ahora Tabular options
(botón amarillo) Inverse CDF.
La opción Pane Options que nos aparecerá al pulsar el botón derecho del ratón nos
permitirá trabajar con las probabilidades que nos interesen.
Generación de números aleatorios.
Tabular Options (botón amarillo) Random Numbers botón derecho del
ratón Pane Options le decimos la cantidad de números aleatorios que queremos
generar de la distribución seleccionada pulsamos el cuarto botón de la ventana
(Save), marcamos save (en Target variable introducimos el nombre de la variable)
y OK.
Si en algún momento queremos ver los datos que hemos
generado, lo podemos hacer acudiendo a la ventana donde
normalmente se introducen los valores de los datos.
Si quisiéramos comprobar si estos datos generados aleatoriamente u otros
obtenidos por otros medios (datos reales), siguen una determinada distribución,
tendríamos muchas alternativas para comprobarlo. Algunas las podemos encontrar en:
Describe > Distribution Fitting > Uncensored data. Tanto en tabular options (botón
amarillo) como en graphical options (botón azul) tenemos muchas opciones entre las
que elegir (si quieres saber que calcula cada una, consulta la ayuda). En esta práctica
escogeremos: graphical options > frequency histogram. Con esta opción, se dibuja el
histograma de los datos y se superpone la función de densidad teórica que hayamos
elegido (caso continuo).
**Vamos a comprobar que los modelos Binomial y Poisson se aproximan al Normal.
(Denotamos por d, los 4 últimos dígitos de tu DNI. Si tu DNI es: 12345678 d=5678 )
(a) Comprobemos que Po(d) se aproxima a N(d,
d ) si d es grande.
Plot > Probability Distributions > Poisson pane options Mean= d OK
botón derecho (sobre gráfico) graphics options X-axis From:
To:
By:
Elegimos ahora el modelo Normal. Pane options Mean=d Std.desvi.=d
(b) Vamos a comprobar que Bi(n=d, p=0,5), se aproxima a N(d·0,5,
PRÁCTICA 3: Distribuciones.
3
d ·0.5·0.5 ).
PRÁCTICAS DE STATGRAPHICS
IG12: ESTADÍSTICA DE ITIG. PRÁCTICAS DE STATGRAPHICS.
PRÁCTICA 3: DISTRIBUCIONES. PROBLEMAS
Nombre y Apellidos............................................................... Grupo ....
Los gráficos y las tablas de frecuencias que no caben en su apartado,
incluirlos en la parte de atrás del folio o en otro folio.
1. Contesta a las siguientes preguntas respecto de la distribución de probabilidad
Normal ( El primer valor del paréntesis es la media, y el segundo la desviación típica):
a) Dibuja la función de densidad de la N(0,1). Seguidamente añade la
N(0,0.5). Por último añade la N(0,3) ¿Qué observas?
plot>probability distributions
aparece una pantalla de diálogo en
la que está preseleccionada la distribución normal. Con el botón de
la derecha y en analysis options, colocamos el valor de la media y
de la desviación típica.
Una vez dado al ok, en el botón de graphical options para calcular
la función de densidad seleccionamos Density/Mass funtion
b) Dibuja ahora la función de distribución de una N(25,1), añade N(25,3.5) y
N(25,21). Modifica los límites del eje x a: -35, +85. ¿Qué observas?
plot>probability distributions>analysis options, colocamos el valor
de la media y de la desviación típica.
graphical options>CDF
Para modificar los límites del eje X, pinchamos, en la gráfica
ampliada a toda la pantalla, sobre los números del eje X hasta que
aparezcan unos puntos amarillos sobre los números. Con el botón de
la derecha pinchamos en axis scaling options, y en él podemos
modificar los valores. Puede ocurrir que no deje hacer esta
modificación (too many tickmarks), es porque el paso de escala es
muy pequeño (by), y hay que ponerlo mayor.
c) Utilizando la función de distribución de N(25,21) anota el valor aproximado
de F(40) y F(10).
F(x) es la función de distribución, que por definición es F(x)=P(X<x).
La forma de calcularla es la siguiente:
plot > probability distributions > tabular options > cumulative
distributions, en él con pane options puedo cambiar el valor de la
variable, y con analysis options la media y la desviación típica del
modelo.
PRÁCTICA 3: Distribuciones.
4
PRÁCTICAS DE STATGRAPHICS
-
Esta opción calcula F(x)=P(X<x) (lower tail area),
P(X=x)(Probability density), y P(X>x) (Uper tail area). La
probabilidad que nos piden es F(x)=P(Xx) y esta la
calculamos:
si la variable es continua, miraremos solo el “lower tail area” y
ya tenemos el valor de F(x)
si la variable es discreta, tendremos que sumar a este valor , la
probabilidad “probability density” (=)
2. Trabaja con la distribución Normal (N(media, desviación típica))
1.a Para la función N(d,1), ¿qué relación hay entre los valores siguientes dos a dos?
P(X d – 1) =
P(X>d+1)=
; f(d + 1)=
f(d – 1)=
.
Relación:
; ¿Por qué?
.
1.b Dibuja la función de densidad de N(d,1), N(d, 0.5) y N(d,3) en una misma gráfica.
¿Qué observas?
.
1.c Dibuja la función de densidad de N(d,1), N(d + 10,1), N(d - 5,1) en una misma gráfica.
¿Qué observas?
.
3. . Contesta a las siguientes preguntas respecto de la distribución de probabilidad
Poisson:
a) Dibuja la distribución de probabilidad de un modelo de Poisson de medias 2,
5, 10 ¿Qué ocurre al aumentar la media?
b) Compara que una Poisson de media 25 se aproxima a una N(25,5). ¿Qué
ilustra ese resultado?
plot>probability
distributions>
(distribución
options para cambiar la media.
graphical options > Density/Mass funtion
PRÁCTICA 3: Distribuciones.
5
Poisson)analysis
PRÁCTICAS DE STATGRAPHICS
4. Trabaja con la distribución Poisson (Po(media))
2.a Sea X Po(2). Calcula P(X=1)=
, P(X<1)=
, P(X=2)=
,
P(X 2)=
, P(X<3)=
, P(X3)=
.
2.b Dibuja la función de probabilidad para las medias: 2, 5,10, a la vez; ¿qué observas?
.
5. Contesta a las siguientes preguntas respecto de la distribución de probabilidad
Binomial (La Binomial tiene dos parámetros n (trial), p (probability), que en la teoría no
se colocan en el mismo orden que en el programa):
a) Dibuja una Bi(10,0.1), Bi(10,0.5) y Bi(10,0.9). Idem para n = 50. ¿Qué ocurre
al ir aumentando el tamaño de n?
b) Calcula aproximadamente para Bi(50,0.1): p(X2) y p(X9).
c) Comprueba que Bi(50,0.1) se aproxima a una Po(5).
plot>probability
distributions>
(distribución
Binomial)analysis
options para cambiar el valor de n, y de p.
graphical options > Density/Mass funtion
Para calcular probabilidades, dentro del análisis anterior tabular
options > cumulative distributions (hay que tener en cuenta que
estamos en una distribución discreta, y la explicación está en el
ejercicio 2).
Para comparar, hacerlo gráficamente.
6. Contesta a las siguientes preguntas respecto de la distribución de probabilidad
Uniforme:
a) Dibuja la función de densidad de los siguientes modelos uniformes: U(0,1),
U(0,5) y U(4,6). ¿Qué observas?
b)Haz lo mismo para las exponenciales: exp(0.5), exp(1) y exp(2). ¿Qué
observas?
7. Calcula el valor de xo para:
a)
X N(0,1), p(Xxo) = 0.95, p(Xxo) = 0.05, p(X>xo) = 0.05.
b)
X 2 20, p(X>xo) = 0.05, p(X>xo) = 0.95
PRÁCTICA 3: Distribuciones.
6
PRÁCTICAS DE STATGRAPHICS
c)
X t15, p(X>xo) = 0.01, p(X>xo) = 0.99
d)
X U(8,12), p(Xxo) = 0.05
Las dos variables nuevas que aparecen son la Chi-square y la
Students-t,
que
aparecen
en
el
menú
de
modelos
de
probabilidad. Para las dos, y con el botón de la derecha,
analysis options, podemos modificar los grados de libertad.
plot>probability
distributions>
colocamos
la
distribución
adecuada>tabular options>inverse CDF aquí introducimos el valor de
la probabilidad y el análisis nos proporciona el valor de x0. Hay
que tener en cuenta que la probabilidad que calculamos es P(Xx),
por lo que si queremos calcular P(X>x) = 1 – P(Xx), y el cálculo lo
hacemos fuera del statgraphics.
8. Una centralita recibe unas 300 llamadas cada hora. No puede establecerse más de
12 conexiones por minuto. Se pide:
a)
Probabilidad de que quede rebasada en un minuto dado.
b)
Probabilidad de que reciba una sola llamada en un minuto dado.
Para contestar a este problema hay que definir la variable y la
distribución de la variable: X = {número de llamadas que recibe una
centralita por minuto}~ Po(300/60). A partir de esto, se pueden contestar
las preguntas:
a)P(X>12)=
b)P(X=1)=
9. Se ha comprobado que la duración de vida de ciertos elementos sigue una
distribución exponencial con media 8 meses. Se pide:
a) Calcular la probabilidad de que un elemento tenga una vida entre 5 y 12
meses.
b) El percentil 0.9 de la distribución.
a)P(5<X<12) = P(X<12)- P(x<5).
b)Para calcular percentiles, dentro del análisis adecuado,
options>inverse CDF, y con el botón de la derecha, modificamos.
PRÁCTICA 3: Distribuciones.
7
tabular
PRÁCTICAS DE STATGRAPHICS
10. En un centro de salud cada médico atiende una media de 6 pacientes en una
hora.
a) ¿ Cuántos pacientes atenderá por termino medio un médico en los 10
primeros minutos de consulta?
b) Calcular la probabilidad de que pase más de un minuto sin que un médico
atienda a un paciente.
c) Si el centro de salud dispone de 50 médicos, ¿cuál es la probabilidad de
que en una hora se atiendan más de 280 pacientes?
Para contestar a este problema hay que definir la variable, para cada
apartado y la distribución de probabilidad de la variable:
a) X = {número de pacientes que se atienden en 10 minutos, por un médico}~
Po(6/6). A partir de esto, se pueden contestar las preguntas.
b) X = {número de pacientes que se atienden en 1 minutos, por un médico}~
Po(6/60)
c) X = {número de pacientes que se atienden en 1 hora, por los 50
médicos}~ Po(6*50)
PRÁCTICA 3: Distribuciones.
8